Bài 3: Góc nội tiếp - trang 73 Toán 9 Tập 2
Bài 3: Góc nội tiếp
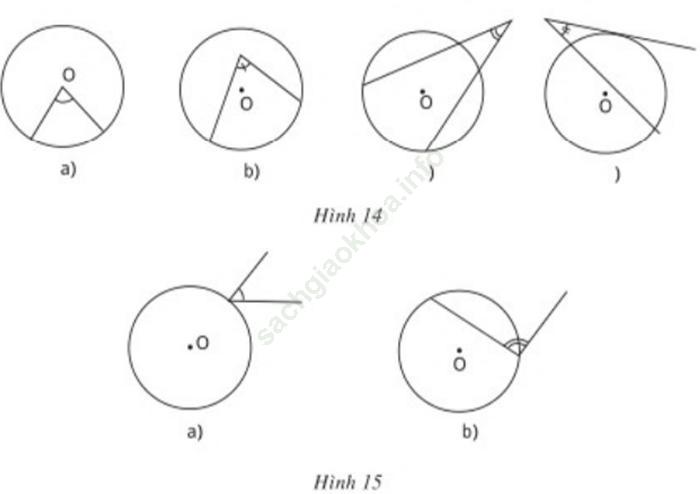
Trả lời câu hỏi Toán 9 Tập 2 Bài 3 trang 73: Vì sao các góc ở hình 14 và hình 15 không phải là góc nội tiếp?
Hướng dẫn giải:
Các góc trên hình 14 không phải góc nội tiếp vì: Các góc này không có đỉnh nằm trên đường tròn.
Các góc trên hình 15 không phải góc nội tiếp vì: Các góc này không có hai cạnh chứa hai dây cung của đường tròn.
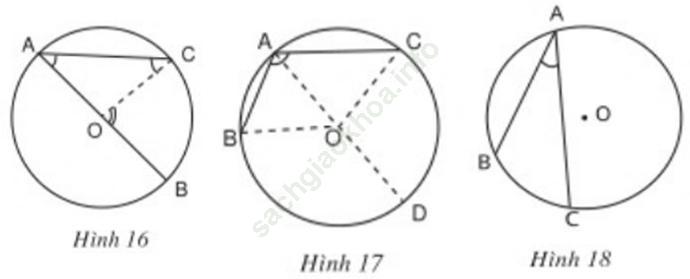
Trả lời câu hỏi Toán 9 Tập 2 Bài 3 trang 73: Bằng dụng cụ, hãy so sánh số đo của góc nội tiếp ∠ (BAC) với số đo của cung bị chắn BC trong mỗi hình 16,17,18 dưới đây.
Hướng dẫn giải:
Số đo của góc nội tiếp ∠ (BAC) bằng một nửa của cung bị chắn BC
Trả lời câu hỏi Toán 9 Tập 2 Bài 3 trang 75: Hãy vẽ hình minh họa các tính chất trên.
Hướng dẫn giải:a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau
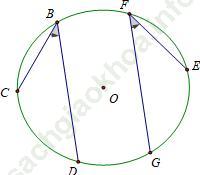
b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau
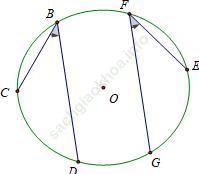
c) Góc nội tiếp (nhỏ hơn hoặc bằng 90o) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung
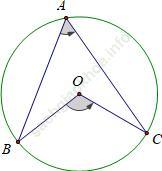
d) Góc nội tiếp chắn nửa đường tròn là góc vuông
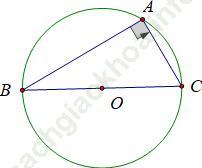
Bài 15 trang 75 SGK Toán 9 Tập 2: Các khẳng định sau đây là đúng hay sai?
a) Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.
b) Trong một đường tròn, các góc nội tiếp bằng nhau thì cùng chắn một cung.
Hướng dẫn giải:
a) Khẳng định trên là Đúng (theo hệ quả b).
b) Khẳng định trên là Sai. Vì:
+) Trong cùng một đường tròn, các góc nội tiếp cùng chắn 1 cung hoặc chắn các cung bằng nhau thì bằng nhau.
+) Trong một đường tròn, các góc nội tiếp bằng nhau chưa chắc cùng chắn một cung.
Kiến thức áp dụng:
Định lý: Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
Hệ quả: Trong một đường tròn, các góc nội tiếp bằng nhau chắn các cung bằng nhau.
Bài 16 trang 75: Xem hình 19 (hai đường tròn có tâm là B, C và điểm B nằm trên đường tròn tâm C).
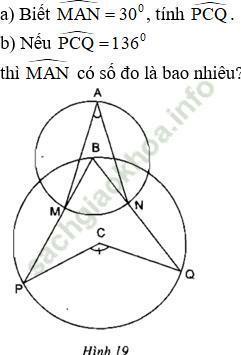
Hướng dẫn giải:
a) Đường tròn tâm B có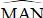 
là góc nội tiếp chắn cung 
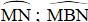là góc ở tâm chắn cung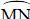 
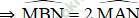
Đường tròn tâm C có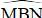 
là góc nội tiếp chắn cung 
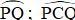là góc ở tâm chắn cung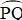 
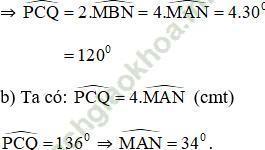
Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
Bài 17 trang 75: Muốn xác định tâm của một đường tròn mà chỉ dùng êke thì phải làm như thế nào?
Hướng dẫn giải: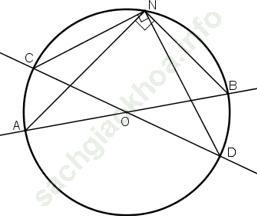
Áp dụng hệ quả: Góc nội tiếp chắn nửa đường tròn là góc vuông.
Cách xác định tâm đường tròn như sau:
+ Đặt đỉnh vuông của eke trùng với một điểm N bất kỳ trên đường tròn, kẻ đường thẳng đi qua cạnh còn lại cắt đường tròn tại A và B ta được đường kính AB.
+ Vẫn đặt đỉnh vuông của eke tại N, xoay eke theo góc khác, kẻ đường thẳng đi qua cạnh còn lại cắt đường tròn tại C và D ta được đường kính CD.
+ CD cắt AB tại tâm O của đường tròn.
Bài 18 trang 75: Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn PQ. Bóng được đặt ở các vị trí A, B, C trên một cung tròn như hình 20.
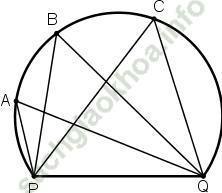
Hãy so sánh các góc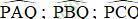 
Hướng dẫn giải:
Các điểm A, B, C, Q, P cùng thuộc một đường tròn.
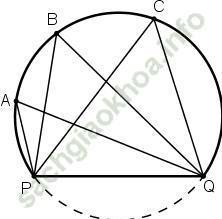
Các góc 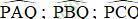đều là các góc nội tiếp cùng chắn cung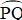 
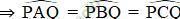
+ Trong cùng một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.