Luyện tập trang 38-39 SGK Toán 9 Tập 2

Luyện tập (trang 38-39)

Bài 6 (trang 38 SGK Toán 9 tập 2): Cho hàm số y = f (x) = x².

a) Vẽ đồ thị của hàm số đó.

b) Tính các giá trị f (-8); f (-1,3); f (-0,75); f (1,5).

c) Dùng đồ thị để ước lượng các giá trị (0,5)²; (-1,5)²; (2,5)².

d) Dùng đồ thị để ước lượng vị trí các điểm trên trục hoành biểu diễn các số √ 3; √ 7.

Hướng dẫn giải:

a) Ta có bảng giá trị:

x	-2	-1	0	1	2
y = x2	4	1	0	1	4

Vẽ đồ thị hàm số:

Trên hệ trục tọa độ xác định các điểm (-2; 4); (-1; 1); (0; 0); (1; 1); (2; 4). Vẽ đường cong đi qua các điểm trên ta được đồ thị hàm số y = x².

b) f (-8) = (-8)² = 64

f (-1,3) = (-1,3)² = 1,69

f (-0,75) = (-0,75)² = 0,5625

f (1,5) = (1,5)² = 2,25.

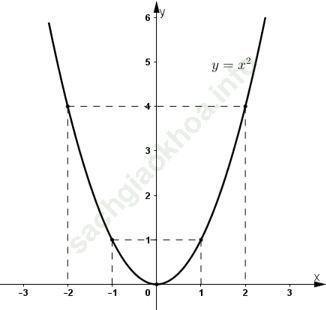
c)

Trên đồ thị hàm số, lấy các điểm M, N, P có hoành độ lần lượt bằng -1,5; 0,5 và 2,5.

Dựa vào đồ thị nhận thấy các điểm M, N, P có tọa độ là: M (-1,5; 2,25); N (0,5; 0,25); P (2,5; 6,25).

Vậy (0,5)² = 2,25; (-1,5)² = 2,25; (2,5)² = 6,25.

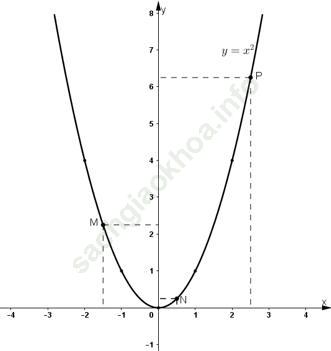
d)

Ta có: (√3)² = 3; (√7)² = 7

⇒ Các điểm (√3; 3) và (√7; 7) thuộc đồ thị hàm số y = x².

Để xác định các điểm √3; √7 trên trục hoành, ta lấy trên đồ thị hàm số các điểm A, B có tung độ lần lượt là 3 và 7.

Chiếu vuông góc các điểm A, B trên trục hoành ta được các điểm √3; √7 trên đồ thị hàm số.

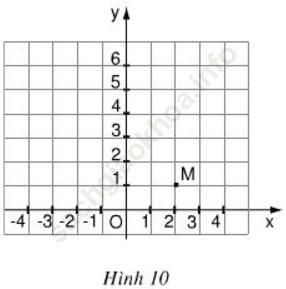
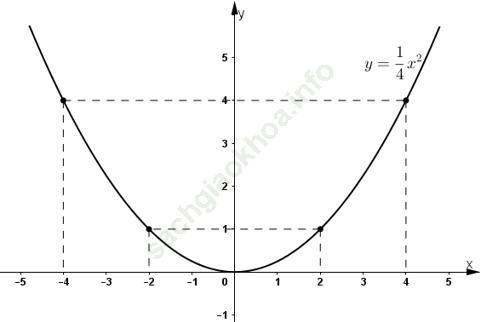
Bài 7 (trang 38): Trên mặt phẳng tọa độ (h. 10), có một điểm M thuộc đồ thị của hàm số y = ax².

a) Tìm hệ số a.

b) Điểm A (4; 4) có thuộc đồ thị không?

c) Hãy tìm thêm hai điểm nữa (không kể điểm O) để vẽ đồ thị.

Hướng dẫn giải:

a) Dựa trên hình 10 ta thấy điểm M có tọa độ (2; 1).

M thuộc đồ thị hàm số y = ax²

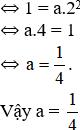
b) Với x = 4 ta có

Vậy điểm A (4; 4) thuộc đồ thị hàm số

c) Chọn x = -2 ⇒

Vậy (-2; 1) thuộc đồ thị hàm số.

Chọn x = -4 ⇒

Vậy (-4; 4) thuộc đồ thị hàm số.

* Vẽ đồ thị:

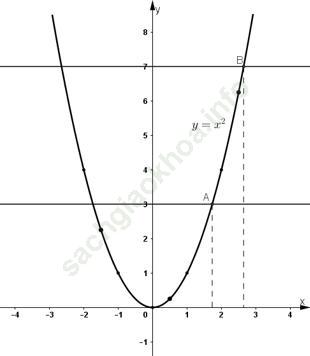
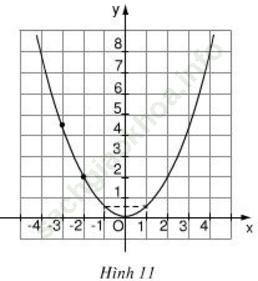
Bài 8 (trang 38): Biết rằng đường cong trong hình 11 là một parapol y = ax².

a) Tìm hệ số a.

b) Tìm tung đệ của điểm thuộc parapol có hoành độ x = -3.

c) Tìm các điểm thuộc parapol có tung độ y = 8.

Hướng dẫn giải:

a) Ta có đồ thị hàm số y = ax² đi qua điểm (-2; 2)

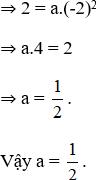
b) Tại x = -3 ta có:

Vậy điểm có hoành độ x = -3 thì tung độ bằng 4,5.

c) Ta có: y = 8 ⇔ ⇔ x² = 16 ⇔ x = 4 hoặc x = -4.

Vậy các điểm thuộc parabol có tung độ bằng 8 là (4; 8) và (-4; 8).

Bài 9 (trang 39): Cho hai hàm số và y = -x + 6.

a) Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ.

b) Tìm tọa độ các giao điểm của hai đồ thị đó.

Hướng dẫn giải:

a)

- Vẽ đường thẳng y = -x + 6

Cho x = 0 ⇒ y = 6 được điểm (0,6)

Cho y = 0 ⇒ x = 6 được điểm (6,0)

⇒ Đường thẳng y = -x + 6 đi qua các điểm (6; 0) và (0; 6).

- Lập bảng giá trị và vẽ đồ thị hàm số

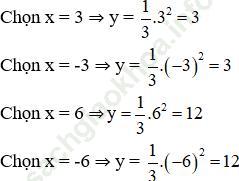
⇒ Parabol đi qua các điểm (3; 3); (-3; 3); (-6; 12); (6; 12); (0; 0).

b) Dựa vào đồ thị ta nhận thấy giao điểm của hai đồ thị là A (-6; 12) và (3; 3).

Bài 10 (trang 39): Cho hàm số y = -0,75x². Qua đồ thị của hàm số đó, hãy cho biết khi x tăng từ -2 đến 4 thì giá trị nhỏ nhất và giá trị lớn nhất của y là bao nhiêu?

Hướng dẫn giải:

- Lập bảng giá trị:

x	-4	-2	0	2	4
y = -0,75x2	-12	-3	0	-3	-12

- Vẽ đồ thị:

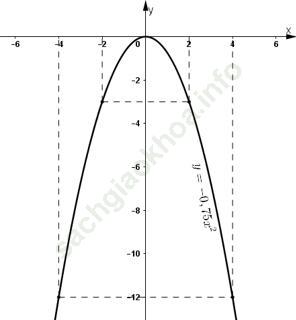
- Quan sát đồ thị hàm số y = -0,75x²:

Khi x tăng từ -2 đến 4, y tăng từ -3 đến 0 rồi lại giảm xuống -12.

Vậy: Giá trị nhỏ nhất của y = -12 đạt được khi x = 4

Giá trị lớn nhất của y = 0 đạt được khi x = 0.

Bài trước: Bài 2: Đồ thị hàm số y = ax2 (a ≠ 0) - trang 34 Toán 9 Tập 2 Bài tiếp: Bài 3: Phương trình bậc hai một ẩn - trang 40 Toán 9 Tập 2