Luyện tập trang 126 - SGK Toán 9 Tập 2
Bài 35 trang 126 SGK Toán 9 Tập 2:
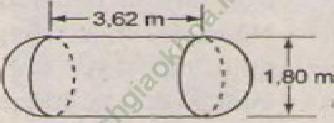
Một cái bồn chứa xăng gồm hai nửa hình cầu và một hình trụ (h. 110).
Hãy tính thể tích của bồn chứa theo các kích thước cho trên hình vẽ.
Hướng dẫn giải:
Thể tích cần tính gồm một hình trụ và hai nửa hình cầu.
+) Hình cầu có đường kính d = 1,8m ⇒ bán kính R = 0,9m
+) Hình trụ có bán kính đáy bằng bán kính hình cầu R = 0,9m; chiều cao h = 3,62m.
=> Thể tích hình trụ: V1 = π. R2.h ≈ 9,21 (m3).
=> Thể tích hai nửa hình cầu: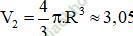 
(m3).
=> Thể tích bồn chứa xăng: V = V1 + V2 ≈ 12,26 (m3).
+ Thể tích hình trụ có bán kính đáy R, chiều cao h là:
+ Thể tích khối cầu có bán kính R là: 
Bài 36 trang 126:
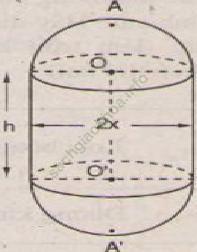
Một chi tiết máy gồm một hình trụ và hai nửa hình cầu với các kích thước đã cho trên hình 111 (đơn vị: cm).
a) Tìm một hệ thức giữa x và h khi AA' có độ dài không đổi và bằng 2a.
b) Với điều kiện ở a), hãy tính diện tích bề mặt và thể tích của chi tiết máy theo x và a.
Hướng dẫn giải:
a) Ta có: AA’ = AO + OO’ + O’A’
hay 2a = x + h + x
hay 2x + h = 2a.
b) Diện tích cần tính gồm diện tích xung quanh của hình trụ có bán kính đáy là x, chiều cao là h và diện tích mặt cầu có bán kính là x.
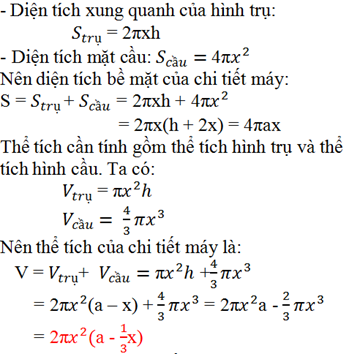
Kiến thức áp dụng:
+ Diện tích xung quanh hình trụ chiều cao h, bán kính đáy R là:
+ Thể tích khối trụ chiều cao h, bán kính đáy R là: V = π. R2.h
+ Diện tích xung quanh mặt cầu có bán kính R là: S = 4π. R2.
+ Thể tích khối cầu có bán kính R là: 
Bài 37 trang 126: Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.
a) Chứng minh rằng MON và APB là hai tam giác vuông đồng dạng.
b) Chứng minh AM. BN = R2
c) Tính tỉ số: 
d) Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra.
Hướng dẫn giải: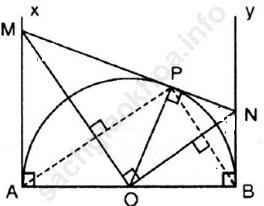
a) Ta có OM, ON lần lượt là tia phân giác của AOP, BOP (tính chất của hai tiếp tuyến cắt nhau).
Mà AOP kề bù với BOP nên suy ra OM vuông góc với ON.
Vậy Δ MON vuông tại O.
Góc 
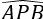là góc nội tiếp chắn nửa đường tròn nên = 900
Tứ giác AOPM có:
Suy ra, tứ giác AOPM nội tiếp đường tròn.
Xét ∆ MON và ∆ APB có:
=> ∆ MON và ∆ APB đồng dạng
b)
* Tam giác MON vuông tại O có đường cao OP nên
OP2 = MP. NP (1)
* Theo tính chất hai tiếp tuyến cắt nhau ta có
MA= MP và NB = NP (2)
Từ (1) và (2) suy ra: OP2 = MA. NB hay R2 = MA. NB (đpcm)
c) * Theo a, ∆ MON và ∆ APB đồng dạng với nhau với tỉ số đồng dạng là:
d) Nửa hình tròn APB quay quanh AB tạo ta hình cầu có bán kính R nên thể tích khối cầu tạo ra là:
