Luyện tập trang 56-57 SGK Toán 9 Tập 2
Bài 37 trang 56 SGK Toán 9 Tập 2: Giải phương trình trùng phương:
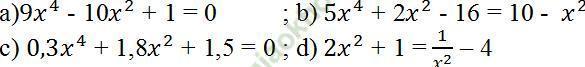
Hướng dẫn giải:
a) 9x4 – 10x2 + 1 = 0 (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành: 9t2 – 10t + 1 = 0 (2)
Giải (2):
Có a = 9; b = -10; c = 1
⇒ a + b + c = 0
⇒ Phương trình (2) có nghiệm t1 = 1; t2 = c/a = 1/9.
Cả hai nghiệm đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x2 = 1 ⇒ x = 1 hoặc x = -1.
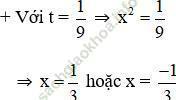
Vậy phương trình (1) có tập nghiệm 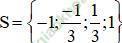
b) 5x4 + 2x2 – 16 = 10 – x2
⇔ 5x4 + 2x2 – 16 – 10 + x2 = 0
⇔ 5x4 + 3x2 – 26 = 0 (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành: 5t2 + 3t – 26 = 0 (2)
Giải (2):
Có a = 5; b = 3; c = -26
⇒ Δ = 32 – 4.5. (-26) = 529 > 0
⇒ Phương trình có hai nghiệm phân biệt
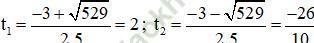
Đối chiếu điều kiện chỉ có t1 = 2 thỏa mãn
+ Với t = 2 ⇒ x2 = 2 ⇒ x = √2 hoặc x = -√2.
Vậy phương trình (1) có tập nghiệm S = {-√2; √2}
c) 0,3x4 + 1,8x2 + 1,5 = 0 (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó, (1) trở thành: 0,3t2 + 1,8t + 1,5 = 0 (2)
Giải (2):
có a = 0,3; b = 1,8; c = 1,5
⇒ a – b + c = 0
⇒ Phương trình có hai nghiệm t1 = -1 và t2 = -c/a = -5.
Cả hai nghiệm đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
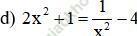
Điều kiện xác định: x ≠ 0.
Quy đồng, khử mẫu ta được:
2x4 + x2 = 1 – 4x2
⇔ 2x4 + x2 + 4x2 – 1 = 0
⇔ 2x4 + 5x2 – 1 = 0 (1)
Đặt t = x2, điều kiện t > 0.
Khi đó (1) trở thành: 2t2 + 5t – 1 = 0 (2)
Giải (2):
Có a = 2; b = 5; c = -1
⇒ Δ = 52 – 4.2. (-1) = 33 > 0
⇒ Phương trình có hai nghiệm phân biệt:
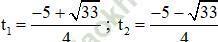
Đối chiếu với điều kiện thấy có nghiệm t1 thỏa mãn.
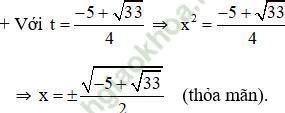
Vậy phương trình có tập nghiệm 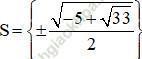
+ Phương trình có dạng: ax4 + bx2 + c = 0 (a ≠ 0) gọi là phương trình trùng phương.
Cách giải phương trình trùng phương:
Bước 1: Đặt x2 = t; t ≥ 0. Khi đó ta đưa được phương trình ban đầu về phương trình bậc hai ẩn t.
Bước 2: Giải phương trình bậc hai ẩn t, đối chiếu với điều kiện t ≥ 0.
Bước 3: Từ nghiệm t vừa tìm được, ta thay trở lại x2 = t để tìm x và kết luận nghiệm.
+ Giải phương trình chứa ẩn ở mẫu thức:
Bước 1: Tìm điều kiện xác định của phương trình.
Bước 2: Quy đồng, khử mẫu
Bước 3: Giải phương trình nhận được
Bước 4: Đối chiếu nghiệm thu được với điều kiện xác định và kết luận nghiệm.
Bài 38 trang 56: Giải các phương trình:
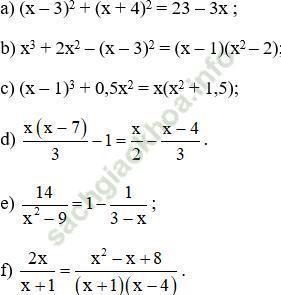
Hướng dẫn giải:
a) (x – 3)2 + (x + 4)2 = 23 – 3x
⇔ x2 – 6x + 9 + x2 + 8x + 16 = 23 – 3x
⇔ x2 – 6x + 9 + x2 + 8x + 16 + 3x – 23 = 0
⇔ 2x2 + 5x + 2 = 0
Có a = 2; b = 5; c = 2 ⇒ Δ = 52 – 4.2.2 = 9 > 0
⇒ Phương trình có hai nghiệm:
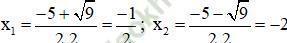
Vậy phương trình có tập nghiệm 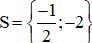
b) x3 + 2x2 – (x – 3)2 = (x – 1)(x2 – 2)
⇔ x3 + 2x2 – (x2 – 6x + 9) = x3 – x2 – 2x + 2
⇔ x3 + 2x2 – x2 + 6x – 9 – x3 + x2 + 2x – 2 = 0
⇔ 2x2 + 8x – 11 = 0.
Có a = 2; b = 8; c = -11 ⇒ Δ’ = 42 – 2. (-11) = 38 > 0
⇒ Phương trình có hai nghiệm:
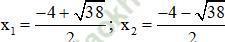
Vậy phương trình có tập nghiệm 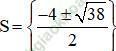
c) (x – 1)3 + 0,5x2 = x (x2 + 1,5)
⇔ x3 - 3x2 + 3x – 1 + 0,5x2 = x3 + 1,5x
⇔ x3 + 1,5x – x3 + 3x2 – 3x + 1 – 0,5x2 = 0
⇔ 2,5x2 – 1,5x + 1 = 0
Có a = 2,5; b = -1,5; c = 1
⇒ Δ = (-1,5)2 – 4.2,5.1 = -7,75 < 0
Vậy phương trình vô nghiệm.
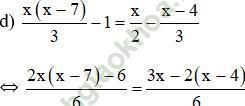
⇔ 2x (x – 7) – 6 = 3x – 2 (x – 4)
⇔ 2x2 – 14x – 6 = 3x – 2x + 8
⇔ 2x2 – 14x – 6 – 3x + 2x – 8 = 0
⇔ 2x2 – 15x – 14 = 0.
Có a = 2; b = -15; c = -14
⇒ Δ = (-15)2 – 4.2. (-14) = 337 > 0
⇒ Phương trình có hai nghiệm:
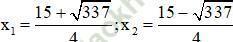
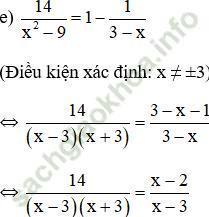
⇔ 14 = (x – 2)(x + 3)
⇔ 14 = x2 – 2x + 3x – 6
⇔ x2 + x – 20 = 0
Có a = 1; b = 1; c = -20
⇒ Δ = 12 – 4.1. (-20) = 81 > 0
Phương trình có hai nghiệm:
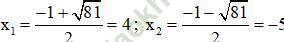
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình có tập nghiệm S = {-5; 4}.
f) Điều kiện: x≠-1; x≠4
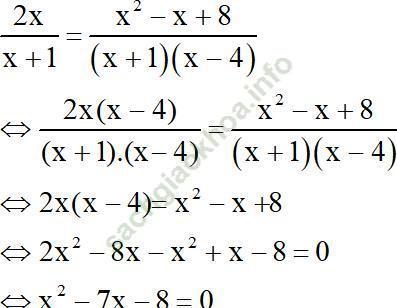
Ta có: a= 1, b = -7, c = - 8
∆ = (-7)2 – 4.1. (- 8)= 81
=> Phương trình có hai nghiệm:
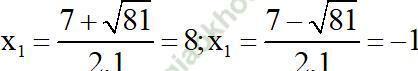
Kết hợp với diều kiện, nghiệm của phương trình đã cho là x = 8
+ Phương trình có dạng: ax4 + bx2 + c = 0 (a ≠ 0) gọi là phương trình trùng phương.
Cách giải phương trình trùng phương:
Bước 1: Đặt x2 = t; t ≥ 0. Khi đó ta đưa được phương trình ban đầu về phương trình bậc hai ẩn t.
Bước 2: Giải phương trình bậc hai ẩn t, đối chiếu với điều kiện t ≥ 0.
Bước 3: Từ nghiệm t vừa tìm được, ta thay trở lại x2 = t để tìm x và kết luận nghiệm.
+ Giải phương trình chứa ẩn ở mẫu thức:
Bước 1: Tìm điều kiện xác định của phương trình.
Bước 2: Quy đồng, khử mẫu
Bước 3: Giải phương trình nhận được
Bước 4: Đối chiếu nghiệm thu được với điều kiện xác định và kết luận nghiệm.
Bài 39 trang 57: Giải phương trình bằng cách đưa về phương trình tích:
a) (3x2 – 7x – 10). [2x2 + (1 – √5)x + √5 – 3] = 0
b) x3 + 3x2 – 2x – 6 = 0;
c) (x2 – 1)(0,6x + 1) = 0,6x2 + x;
d) (x2 + 2x – 5)2 = (x2 – x + 5)2.
Hướng dẫn giải:
a) (3x2 – 7x – 10). [2x2 + (1 – 5)x + 5 – 3] = 0
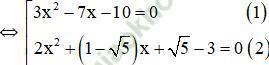
+ Giải (1):
3x2 – 7x – 10 = 0
Có a = 3; b = -7; c = -10
⇒ a – b + c = 0
⇒ (1) có hai nghiệm x1 = -1 và x2 = -c/a = 10/3.
+ Giải (2):
2x2 + (1 - √5)x + √5 - 3 = 0
Có a = 2; b = 1 - √5; c = √5 - 3
⇒ a + b + c = 0
⇒ (2) có hai nghiệm:
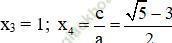
Vậy phương trình có tập nghiệm 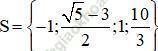
b) x3 + 3x2 – 2x – 6 = 0
⇔ (x3 + 3x2) – (2x + 6) = 0
⇔ x2(x + 3) – 2 (x + 3) = 0
⇔ (x2 – 2)(x + 3) = 0
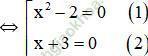
+ Giải (1): x2 – 2 = 0 ⇔ x2 = 2 ⇔ x = √2 hoặc x = -√2.
+ Giải (2): x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm S = {-3; -√2; √2}
c) (x2 – 1)(0,6x + 1) = 0,6x2 + x
⇔ (x2 – 1)(0,6x + 1) = x. (0,6x + 1)
⇔ (x2 – 1)(0,6x + 1) – x (0,6x + 1) = 0
⇔ (0,6x + 1)(x2 – 1 – x) = 0
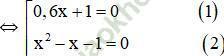
+ Giải (1): 0,6x + 1 = 0 ⇔ 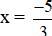
+ Giải (2):
x2 – x – 1 = 0
Có a = 1; b = -1; c = -1
⇒ Δ = (-1)2 – 4.1. (-1) = 5 > 0
⇒ (2) có hai nghiệm 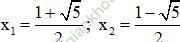
Vậy phương trình có tập nghiệm 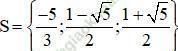
d) (x2 + 2x – 5)2 = (x2 – x + 5)2
⇔ (x2 + 2x – 5)2 – (x2 – x + 5)2 = 0
⇔ [(x2 + 2x – 5) – (x2 – x + 5)]. [(x2 + 2x – 5) + (x2 – x + 5)] = 0
⇔ (3x – 10)(2x2 + x) = 0
⇔ (3x-10).x. (2x+1)=0
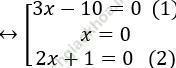
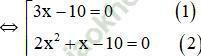
+ Giải (1): 3x – 10 = 0 ⇔ 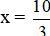
+ Giải (2):
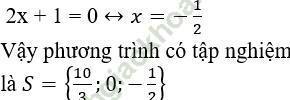
+ Phương trình tích: A (x).B (x).C (x)…. = 0 ⇔
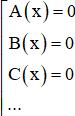
+ Nếu phương trình ax2 + bx + c = 0 (a ≠ 0) có a + b + c = 0 thì phương trình có một nghiệm x1 = 1; nghiệm còn lại x2 = c/a.
+ Nếu phương trình ax2 + bx + c = 0 (a ≠ 0) có a – b + c = 0 thì phương trình có một nghiệm x1 = -1; nghiệm còn lại x2 = -c/a.
Bài 40 (trang 57): Giải phương trình bằng cách đặt ẩn phụ:
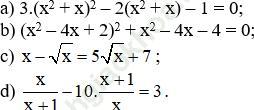
Hướng dẫn:
a) Đặt t = x2 + x, ta có phương trình 3t2 - 2t - 1 = 0. Giải phương trình này, ta tìm được hai giá trị của t. Thay mỗi giá trị của t vừa tìm được vào đẳng thức t = x2 +x, ta được một phương trình của ẩn x. Giải mỗi phương trình này sẽ tìm được giá trị của x.
Bài giải
a) 3. (x2 + x)2 – 2 (x2 + x) – 1 = 0 (1)
Đặt t = x2 + x,
Khi đó (1) trở thành: 3t2 – 2t – 1 = 0 (2)
Giải (2): Có a = 3; b = -2; c = -1
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t1 = 1; t2 = c/a = -1/3.
+ Với t = 1 ⇒ x2 + x = 1 ⇔ x2 + x – 1 = 0 (*)
Có a = 1; b = 1; c = -1 ⇒ Δ = 12 – 4.1. (-1) = 5 > 0
(*) có hai nghiệm
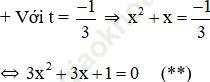
Có a = 3; b = 3; c = 1 ⇒ Δ = 32 – 4.3.1 = -3 < 0
⇒ (**) vô nghiệm.
Vậy phương trình (1) có tập nghiệm
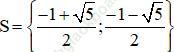
b) (x2 – 4x + 2)2 + x2 – 4x – 4 = 0
⇔ (x2 – 4x + 2)2 + x2 – 4x + 2 – 6 = 0 (1)
Đặt x2 – 4x + 2 = t,
Khi đó (1) trở thành: t2 + t – 6 = 0 (2)
Giải (2): Có a = 1; b = 1; c = -6
⇒ Δ = 12 – 4.1. (-6) = 25 > 0
⇒ (2) có hai nghiệm
+ Với t = 2 ⇒ x2 – 4x + 2 = 2
⇔ x2 – 4x = 0
⇔ x (x – 4) = 0
⇔ x = 0 hoặc x = 4.
+ Với t = -3 ⇒ x2 – 4x + 2 = -3
⇔ x2 – 4x + 5 = 0 (*)
Có a = 1; b = -4; c = 5 ⇒ Δ’ = (-2)2 – 1.5 = -1 < 0
⇒ (*) vô nghiệm.
Vậy phương trình ban đầu có tập nghiệm S = {0; 4}.
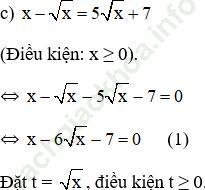
Khi đó (1) trở thành: t2 – 6t – 7 = 0 (2)
Giải (2): Có a = 1; b = -6; c = -7
⇒ a – b + c = 0
⇒ (2) có nghiệm t1 = -1; t2 = -c/a = 7.
Đối chiếu điều kiện chỉ có nghiệm t = 7 thỏa mãn.
+ Với t = 7 ⇒ √ x = 7 ⇔ x = 49 (thỏa mãn).
Vậy phương trình đã cho có nghiệm x = 49.
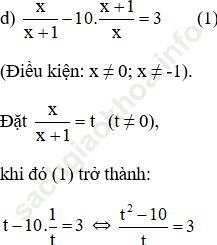
⇔ t2 – 10 = 3t ⇔ t2 – 3t – 10 = 0 (2)
Giải (2): Có a = 1; b = -3; c = -10
⇒ Δ = (-3)2 - 4.1. (-10) = 49 > 0
⇒ (2) có hai nghiệm:
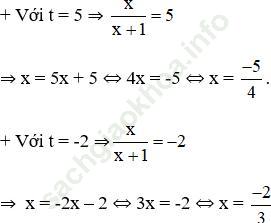
Cả hai nghiệm đều thỏa mãn điều kiện xác định.
Vậy phương trình đã cho có tập nghiệm: