Bài 5: Dấu hiệu nhận biết tiếp tuyến của đường tròn - trang 110 Toán 9 Tập 1

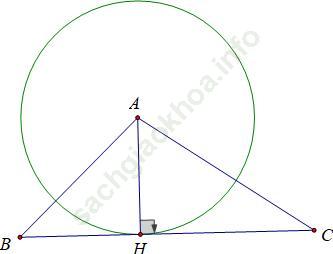
Ta có: BC đi qua điểm H thuộc đường tròn (A; AH)

BC ⊥ AH tại H

⇒ BC là tiếp tuyến của đường tròn (A; AH)

Trả lời câu hỏi Toán 9 Tập 1 Bài 5 trang 111: Hãy chứng minh cách dựng trên là đúng.

Hướng dẫn giải: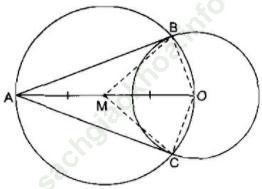

Ta có: MA = MO = MB (cùng bằng bán kính đường tròn tâm M, bán kính MO)

MA = MB ⇒ Δ AMB cân tại M ⇒ ∠ (BAO) = ∠ (ABM)

MO = MB⇒ Δ BMO cân tại M ⇒ ∠ (BOA) = ∠ (MBO)

⇒ ∠ (BAO) + ∠ (BOA) = ∠ (ABM) + ∠ (MBO) = ∠ (ABO) (1)

Mặt khác ta lại có: ∠ (BAO) + ∠ (BOA) + ∠ (ABO) = 180^o (2) (tổng 3 góc trong tam giác)

Từ (1) và (2) ⇒ ∠ (ABO) = 90^o

Hay AB là tiếp tuyến của đường tròn tâm (O), bán kính OB

Chứng minh tương tự, ta được AC là tiếp tuyến của đường tròn tâm (O), bán kính OC

Bài 21 (trang 111 SGK Toán 9 Tập 1): Cho tam giác ABC có AB = 3, AC = 4, BC = 5. Vẽ đường tròn (B; BA). Chứng minh rằng AC là tiếp tuyến của đường tròn.

Hướng dẫn giải: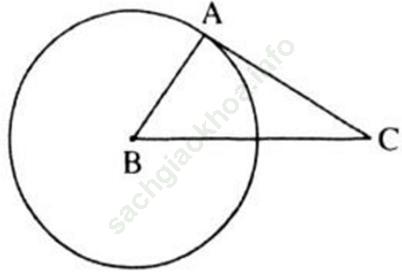

Ta có: AB² + AC² = 3² + 4² = 25

BC² = 5² = 25

Nên: AB² + AC² = BC²

=> tam giác ABC vuông tại A hay AC ⊥ BA.

Đường thẳng AC đi qua điểm A của đường tròn và vuông góc với bán kính BA đi qua điểm A nên AC là tiếp tuyến của đường tròn (đpcm).

Bài 22 (trang 111): Cho đường thẳng d, điểm A nằm trên đường thẳng d, điểm B nằm ngoài đường thẳng d. Hãy dựng đường tròn (O) đi qua điểm B và tiếp xúc với đường thẳng d tại A.

Hướng dẫn giải: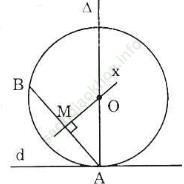

Cách dựng đường tròn như sau:

Đường tròn (O) tiếp xúc với d nên d là tiếp tuyến của (O) hay d vuông góc với bán kính của (O) tại tiếp điểm A.

=> Tâm O của đường tròn nằm trên đường thẳng vuông góc với d tại A.

Lại có (O) qua B nên tâm O của đường tròn nằm trên đường trung trực của AB.

Vậy tâm O là giao điểm của đường vuông góc với d tại A và đường trung trực của AB.

Bài 23 (trang 111): Đố.

Dây cua-roa trên hình 76 có những phần là tiếp tuyến của các đường tròn tâm A, B, C. Chiều quay của đường tròn tâm B ngược chiều quay của kim đồng hồ. Tìm chiều quay của đường tròn tâm A và đường tròn tâm C (cùng chiều quay hay ngược chiều quay của kim đồng hồ).

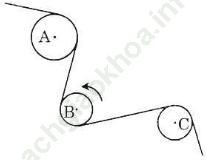
Hình 76

Hướng dẫn giải:

Từ hình vẽ, đường tròn (A) và (C) nằm cùng một phía (về bên dưới) so với sợi dây nên có cùng chiều quay, còn đường tròn (B) nằm ở khác phía (bên trên).

=> đường tròn (A) và (C) quay ngược chiều với (B).

Khi dây cua-roa chuyển động, đường tròn (B) quay ngược chiều của kim đồng hồ nên đường tròn (A) và (C) sẽ quay cùng chiều kim đồng hồ.

Bài 24 (trang 111-112): Cho đường tròn (O), dây AB khác đường kính. Qua O kẻ đường vuông góc với AB, cắt tiếp tuyến tại A của đường tròn ở điểm C.

a) Chứng minh rằng CB là tiếp tuyến của đường tròn.

b) Cho bán kính của đường tròn bằng 15cm, AB = 24 cm. Tính độ dài OC.

Hướng dẫn giải: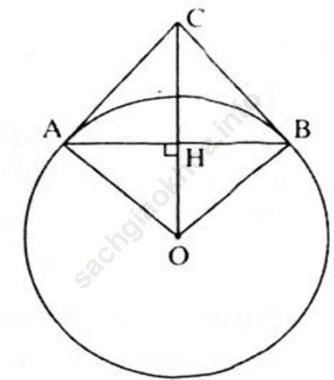

a) Gọi H là giao điểm của OC và AB, Δ AOB cân tại O (OA = OB, bán kính). OH là đường cao nên cũng là đường phân giác. Do đó:

Suy ra: CB vuông góc với OB, mà OB là bán kính của đường tròn (O)

⇒ CB là tiếp tuến của đường tròn (O) tại B. (đpcm)

b) Ta có: OH vuông góc AB nên H là trung điểm của AB (quan hệ vuông góc giữa đường kính và dây)

Vậy OC = 25 cm

Bài 25 (trang 111): Cho đường tròn tâm O có bán kính OA = R, dây BC vuông góc với OA tại trung điểm M của OA.

a) Tứ giác OCAB là hình gì? Vì sao?

b) Kẻ tiếp tuyến với đường tròn tại B, nó cắt đường thẳng OA tại E. Tính độ dài BE theo R.

Hướng dẫn giải: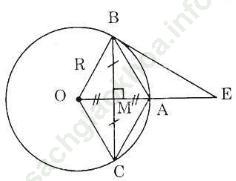

a) Bán kính OA vuông góc với BC nên MB = MC.

Lại có MO = MA (gt).

Suy ra tứ giác OBAC là hình bình hành vì có các đường chéo cắt nhau tại trung điểm mỗi đường.

Lại có: OA ⊥ BC nên OBAC là hình thoi.

b) Ta có: OA = OB (bán kính)

OB = BA (tính chất hình thoi).

Nên OA = OB = BA => Δ AOB đều => ∠ AOB = 60^o

Trong tam giác OBE vuông tại B ta có:

BE = OB. tg∠ AOB = OB. tg60^o = R. √ 3