Bài 7: Vị trí tương đối của hai đường tròn - trang 117 Toán 9 Tập 1
Bài 7: Vị trí tương đối của hai đường tròn
Trả lời câu hỏi Toán 9 Tập 1 Bài 7 trang 117: Ta gọi hai đường tròn không trùng nhau là hai đường tròn phân biệt. Vì sao hai đường tròn phân biệt không thể có quá hai điểm chung?
Hướng dẫn giải:Nếu hai đường tròn có nhiều hơn hai điểm chung thì khi đó hai đường tròn sẽ đi qua ít nhất ba điểm chung. Mà qua 3 điểm phân biệt thì chỉ xác định được duy nhất 1 đường tròn nên 2 đường tròn này không thể phân biệt
Trả lời câu hỏi Toán 9 Tập 1 Bài 7 trang 118:
a) Quan sát hình 85, chứng minh rằng OO’ là đường trung trực của AB.
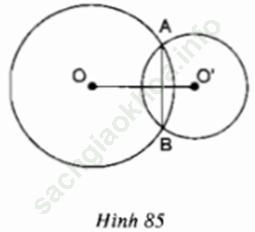
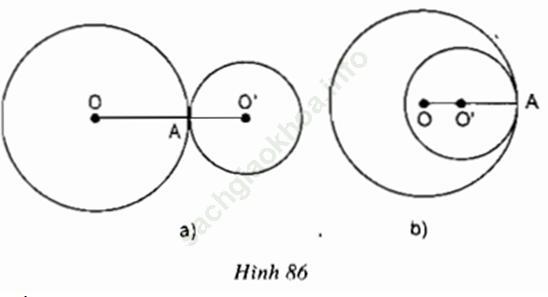
b) Quan sát hình 86, hãy dự đoán về vị trí của điểm A đối với đường nối tâm OO’.
Hướng dẫn giải:
a) Ta có: OA = OB (= bán kính đường tròn (O))
O’A = O’B (= bán kính đường tròn (O’))
⇒ OO’ là đường trung trực của AB
b) Hình 86a) Hai đường tròn tiếp xúc ngoài thì A nằm giữa O và O’
Hình 86b) Hai đường tròn tiếp xúc trong thì A nằm ngoài đoạn OO’
Trả lời câu hỏi Toán 9 Tập 1 Bài 7 trang 119: Cho hình 88.
a) Hãy xác định vị trí tương đối của hai đường tròn (O) và (O’).
b) Chứng minh rằng BC // OO’ và ba điểm C, B, D thẳng hàng.
Hướng dẫn giải: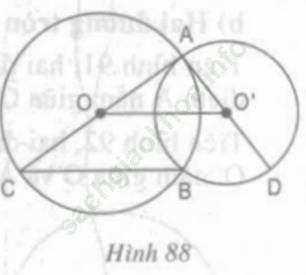
a) Hai đường tròn (O) và (O’) cắt nhau
b) Xét tam giác ABC có:
OA = OB = OC = bán kính đường tròn (O)
Mà BO là trung tuyến của tam giác ABC
⇒ ∆ABC vuông tại B ⇒ AB ⊥ BC (1)
Lại có OO’ là đường trung trực của AB
⇒ AB ⊥ OO' (2)
Từ (1) và (2) ⇒ OO’ // BC
Chứng minh tương tự ta có ∆ABD vuông tại B ⇒ AB ⊥ BD (3)
Từ (1) và (3) ⇒ B, C, D thẳng hàng.
Bài 33 (trang 119 SGK Toán 9 Tập 1): Trên hình 89, hai đường tròn tiếp xúc nhau tại A. Chứng minh rằng OC // O'D.

Hình 89
Hướng dẫn giải:Ta có: OA = OC (bán kính) nên Δ OAC cân tại O.
Lại có O'A = O'D (bán kính) nên Δ O'AD cân tại O'
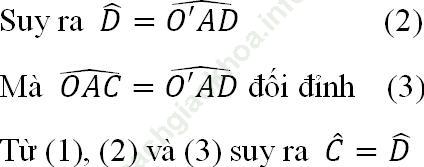
Vậy OC // O'D (có hai góc so le trong bằng nhau).
Bài 34 (trang 119): Cho hai đường tròn (O; 20cm) và (O'; 15cm) cắt nhau tại A và B. Tính đoạn nối tâm OO', biết rằng AB = 24 cm. (Xét hai trường hợp: O và O' nằm khác phía đối với AB; O và O' nằm cùng phía đối với AB).
Hướng dẫn giải:- Trường hợp 1: O và O' nằm khác phía đối với AB
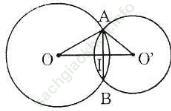
Gọi I là giao điểm của OO' và AB. Theo tính chất đường nối tâm ta có:
AB ⊥ OO' và AI = IB = 12
Áp dụng định lí Pitago, ta được:
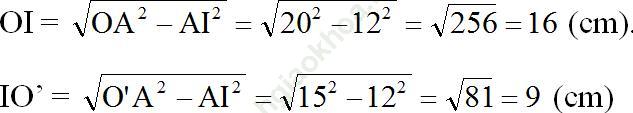
Vậy OO' = OI + IO' = 16 + 9 = 25 (cm)
- Trường hợp 2: O và O' nằm cùng phía đối với AB
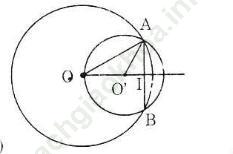
Tương tự như trường hợp 1, ta có:

Vậy OO' = OI – O'I = 16 – 9 = 7 (cm).