Bài 4: Giải hệ phương trình bằng phương pháp cộng đại số - trang 17 Toán 9 Tập 2
Bài 4: Giải hệ phương trình bằng phương pháp cộng đại số
Trả lời câu hỏi Toán 9 Tập 2 Bài 4 trang 17: Áp dụng quy tắc cộng đại số để biến đồi hệ (I), nhưng ở bước 1, hãy trừ từng vế hai phương trình của hệ (I) và viết ra các hệ phương trình mới thu được.
Hướng dẫn giải:
Trừ từng vế hai phương trình của hệ (I) ta được phương trình:
(2x – y) – (x + y) = 1 – 2 hay x – 2y = -1
Khi đó, ta thu được hệ phương trình mới:
Trả lời câu hỏi Toán 9 Tập 2 Bài 4 trang 17: Các hệ số của y trong hai phương trình của hệ (II) có đặc điểm gì?
Hướng dẫn giải:
Hệ số của y trong hai phương trình của hệ (II) đối nhau (tức là có tổng = 0)
Trả lời câu hỏi Toán 9 Tập 2 Bài 4 trang 18:
a) Nêu nhận xét về các hệ số của x trong hai phương trình của hệ (III).
b) Áp dụng quy tắc cộng đại số, hãy giải hệ (III) bằng cách trừ từng vế hai phương trình của (III).
Hướng dẫn giải:
a) Hệ số của x trong hai phương trình của hệ (III) giống nhau
Lấy phương trình thứ nhất trừ đi phương trình thứ hai vế với vế, ta được: 5y = 5
Do đó:
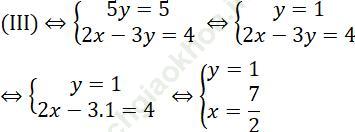
Vậy hệ phương trình có nghiệm duy nhất (7/2; 1)
Trả lời câu hỏi Toán 9 Tập 2 Bài 4 trang 18: Giải tiếp hệ (IV) bằng phương pháp đã nêu ở trường hợp thứ nhất.
Hướng dẫn giải:
Lấy phương trình thứ nhất trừ đi phương trình thứ hai vế với vế, ta được: -5y = 5
Do đó
Vậy hệ phương trình có nghiệm duy nhất (3; -1)
Trả lời câu hỏi Toán 9 Tập 2 Bài 4 trang 18: Nêu một cách khác để đưa hệ phương trình (IV) về trường hợp thứ nhất?
Hướng dẫn giải:
Chia cả 2 vế của phương trình thứ nhất cho 3 và 2 vế của phương trình thứ hai cho 2 ta được:
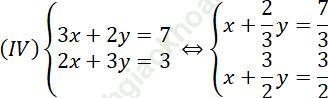
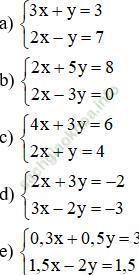
Hướng dẫn giải:
Gợi ý: Hệ số của y ở 2 phương trình đối nhau nên cộng từng vế của phương trình ta được:
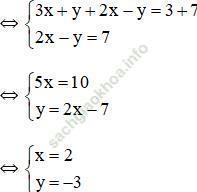
Vậy hệ phương trình có nghiệm duy nhất (2; -3).
Gợi ý: Hệ số của x ở 2 phương trình bằng nhau nên ta trừ từng vế của 2 phương trình
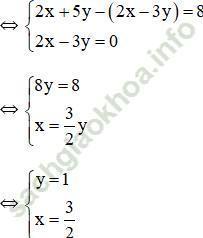
Vậy hệ phương trình có nghiệm duy nhất 
Gợi ý: Nhân cả hai vế của phương trình (2) với 2 để hệ số của x bằng nhau
(Hệ số của x bằng nhau nên ta trừ từng vế của 2 phương trình)
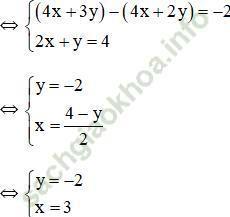
Vậy hệ phương trình có nghiệm duy nhất (3; -2).
Gợi ý: Nhân hai vế phương trình (1) với 2, phương trình (2) với 3 để hệ số của y đối nhau
(Hệ số của y đối nhau nên cộng từng vế hai phương trình).
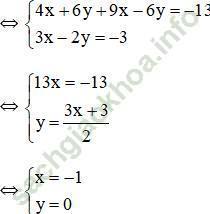
Vậy hệ phương trình có nghiệm duy nhất (-1; 0).
Gợi ý: Nhân hai vế phương trình (1) với 4 để hệ số của y đối nhau.
(Hệ số của y đối nhau nên ta cộng từng vế 2pt)
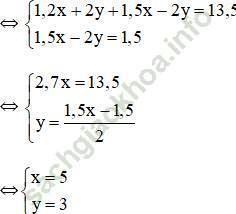
Vậy hệ phương trình có nghiệm duy nhất (5; 3).
Kiến thức áp dụng
Giải hệ phương trình bằng phương pháp cộng đại số
1) Nhân hai vế của phương trình với mỗi hệ số thích hợp (nếu cần) sao cho hệ số của một trong hai ẩn bằng nhau hoặc đối nhau.
2) Áp dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).
3) Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho và kết luận.
Bài 21 trang 19 SGK Toán 9 Tập 2: Giải các hệ phương trình sau bằng phương pháp cộng đại số:
Hướng dẫn giải:
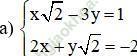
Gợi ý: Chia hai vế của pt 2 cho √2 để hệ số của x bằng nhau)
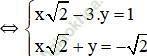
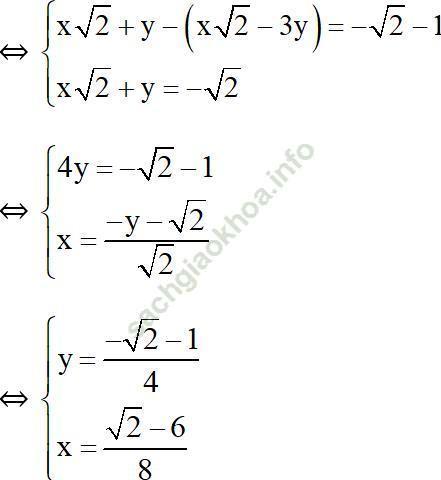
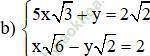
Gợi ý: Chia hai vế phương trình (2) cho √2 để hệ số của y đối nhau
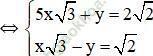
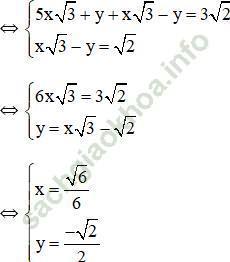
Vậy hệ phương trình có nghiệm duy nhất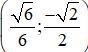 
Giải hệ phương trình bằng phương pháp cộng đại số
1) Nhân hai vế của phương trình với mỗi hệ số thích hợp (nếu cần) sao cho hệ số của một trong hai ẩn bằng nhau hoặc đối nhau.
2) Áp dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).
3) Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho và kết luận.