Ôn tập chương 3 (Câu hỏi - Bài tập) (trang 63 Toán 6 Tập 2)
1. Viết dưới dạng tổng quát của phân số. Cho ví dụ minh họa 1 phân số nhỏ hơn 0,1 phân số bằng 0,1 phân số lớn hơn 0 nhưng bé hơn 1,1 phân số lớn hơn 1.
Trả lời

2. Thế nào là 2 phân số bằng nhau? Cho ví dụ minh họa.
Trả lời
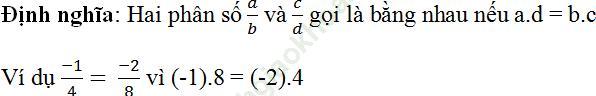
3. Phát biểu tính chất cơ bản của phân số. Giải thích vì sao bất kỳ phân số nào cũng viết dưới dạng một phân số với mẫu dương.
Trả lời
Tính chất cơ bản của phân số:
- Nếu ta nhân cả tử số và mẫu số của 1 phân số với cùng 1 số nguyên khác 0 thì ta sẽ được 1 phân số bằng phân số đã cho.
- Nếu ta chia cả tử số và mẫu số của 1 phân số đã cho cùng 1 ước chung của chúng thì ta được 1 phân số bằng phân số đã cho.
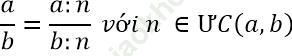
4. Muốn rút gọn phân số ta phải làm như nào? Cho ví dụ minh họa.
Trả lời
Qui tắc: Muốn rút gọn 1 phân số ta chia cả tử số và mẫu số của chúng cho 1 ước chung (khác 1 và -1) của chúng.
5. Thế nào là phân số tối giản? Cho ví dụ minh họa.
Trả lời
Định nghĩa: Phân số tối giản (hay phân số không thể rút gọn được nữa) là phân số mà tử số và mẫu số chỉ có ước chung là 1 và -1.
6. Phát biểu quy tắc quy đồng mẫu số của nhiều phân số.
Trả lời
Quy tắc: Muốn quy đồng mẫu số của nhiều phân số với mẫu số dương ta làm như dưới đây:
Bước 1: Tìm 1 bội chung của các mẫu (thường là bội chung nhỏ nhất) để làm mẫu số chung.
Bước 2: Tìm thừa số phụ của từng mẫu số (bằng cách chia mẫu số chung của từng mẫu số).
Bước 3: Nhân cả tử số và mẫu số của từng phân số với thừa số phụ tương ứng.
7. Muốn so sánh 2 phân số không có cùng mẫu nếu ta làm như nào? Cho ví dụ minh họa.
Trả lời
Quy tắc: Muốn so sánh 2 phân số không có cùng mẫu số ta viết chúng dưới dạng 2 phân số có cùng 1 mẫu dương sau đó so sánh các tử số với nhau: Phân số nào có cùng tử số lớn hơn thì lớn hơn.

8. Phát biểu quy tắc cộng 2 phân số trong trường hợp:
a) Cùng mẫu
b) Không cùng mẫu
Trả lời
a) Cộng 2 phân số có cùng mẫu số
Quy tắc: Muốn cộng 2 phân số có cùng mẫu ta cộng các tử số và giữ nguyên mẫu số
b) Cộng 2 phân số không có cùng mẫu
Quy tắc: Muốn cộng 2 phân số không cùng mẫu số ta viết chúng dưới dạng 2 phân số có cùng một mẫu số sau đó cộng các tử và giữ nguyên mẫu số chung.
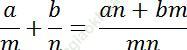
9. Phát biểu những tính chất cơ bản của phép cộng phân số.
Trả lời
Phép cộng phân số có những tính chất cơ bản dưới đây:
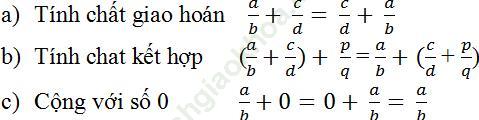
10. a) Viết số đối của phân số
b) Phát biểu quy tắc trừ 2 phân số.
Trả lời

11. Phát biểu quy tắc nhân 2 phân số.
Trả lời
Quy tắc: Muốn nhân 2 phân số ta nhân các tử số với nhau và nhân các mẫu số với nhau:
12. Phát biểu những tính chất cơ bản của phép nhân phân số?
Trả lời
Phép nhân phân số có những tính chất cơ bản dưới đây:

13. Viết số nghịch đảo của phân số a/b (a, b ∈Z, a ≠ 0, b ≠ 0)
Trả lời
14. Phát biểu qui tắc khi thực hiện chia phân số cho phân số.
Trả lời
Quy tắc: Muốn chia 1 phân số cho 1 phân số ta nhân số nghịch đảo của số chia với số bị chia.
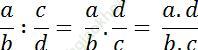
15. Cho ví dụ minh họa về hỗn số. Thế nào là phân số thập phân? Số thập phân? Cho ví dụ minh họa. Viết phân số 9/5 dưới dạng phân số thập phân, hỗn số, số thập phân, phần trăm với ký hiệu %.
Trả lời

- Số thập phân gồm có 2 phần:
+ Phần số nguyên viết bên trái dấu phẩy
+ Phần thập phân viết bên phải dấu phẩy
+ Số chữ số thập phân bằng chữ số 0 ở mẫu số của phân số thập phân

Bài 154 (trang 64 SGK Toán 6 tập 2): Cho phân số x/3. Với giá trị nguyên nào của x thì thỏa mãn điều kiện:
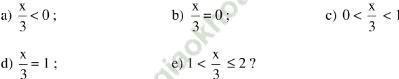
Lời giải:

Bài 155 (trang 64 SGK Toán 6 tập 2): Điền số thích hợp vào các ô vuông:
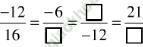
Lời giải:

Bài 156 (trang 64 SGK Toán 6 tập 2): Rút gọn các phân số:
Đáp án:
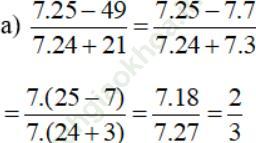
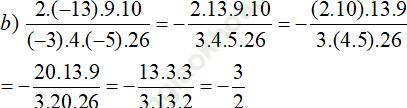
Bài 157 (trang 64 SGK Toán 6 tập 2): Viết các số đo thời gian dưới đây với đơn vị tính là giờ:
15 phút; 45 phút; 78 phút; 150 phút.
Đáp án:Gợi ý: Làm như hướng dẫn ở trong sgk Toán 6 Tập 2, lấy số phút chia cho 60.

Bài 158 (trang 64 SGK Toán 6 tập 2): So sánh hai phân số:
Đáp án:


Bài 159 (trang 64 SGK Toán 6 tập 2): Các phân số dưới đây được sắp xếp theo 1 quy luật. Hãy qui đồng mẫu của các phân số để tìm ra quy luật đó sau đó điền tiếp vào chỗ trống 1 phân số thích hợp:

Đáp án:


Bài 160 (trang 64 SGK Toán 6 tập 2): Tìm phân số a/b bằng phân số 18/27 biết rằng ƯCLN (a, b) = 13.
Đáp án:Ta có:
Vậy phân số tối giản của phân số ![]()
Mà ƯCLN (a; b) = 13 do đó ta có:
a: 13 = 2 suy ra a = 26.
b: 13 = 3 suy ra b = 39.
Vậy phân số cần phải tìm là ![]()
Bài 161 (trang 64 SGK Toán 6 tập 2): Tính giá trị của các biểu thức:
Đáp án:
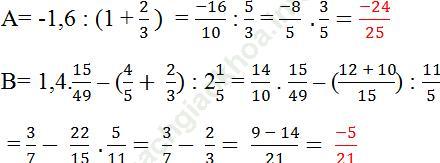
Bài 162 (trang 65 SGK Toán 6 tập 2): Tìm x, biết rằng:
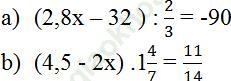
Đáp án:
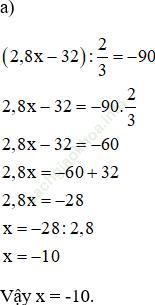
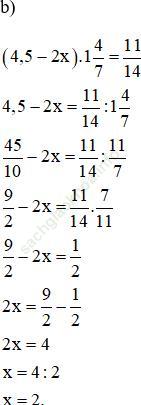
Bài 163 (trang 65 SGK Toán 6 tập 2): 1 cửa hàng bán được 356,5m vải gồm 2 loại vải trắng và vải hoa. Biết rằng số vải hoa bằng 78,25% số vải trắng. Tính số mét vải của từng loại.
Đáp án:Đặt số mét vải trắng là a (m).
Biết rằng số mét vải hoa bằng 78,25% số vải trắng. Do đó số vải hoa bằng: a. 78,25% (mét).
Tổng số mét vải trắng và vải hoa tính theo a là:
a + a. 78,25% = a. 100% + a. 78,25% = a. 178,25% (mét).
Ta có: 178,25% của a tương ứng với 356,5m
Vậy nên:
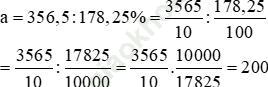
Vậy cửa hàng có 200m vải trắng và 356,5 – 200 = 156,5 m vải hoa
Bài 164 (trang 65 SGK Toán 6 tập 2): Khi trả tiền mua 1 cuốn sách theo đúng giá trên bìa, Oanh đã được cửa hàng trả lại số tiền là 1200đ vì đã được khuyến mãi 10%. Vậy Oanh đã mua cuốn sách đó với giá bao nhiêu?
Phân tích đề
Đây là dạng bài tập Tìm 1 số khi biết giá trị một phân số của nó. Bài toán có thể được hiểu là: Tìm giá của cuốn sách khi biết 10% giá của cuốn sách đó là 1200đ.
Đáp án:Vì 10% giá của cuốn sách đó tương đương với 1200đ nên ta có giá của cuốn sách là:
1200: 10% = 1200: 10/100 = 12 000đ
Vậy Oanh đã mua cuốn sách đó với giá:
12 000 - 1200 = 10 800đ
Bài 165 (trang 65 SGK Toán 6 tập 2): 1 người gửi tiết kiệm 2 triệu đồng tính ra mỗi tháng đã được lãi 11200d. Hỏi người ấy đã gửi tiết kiệm với lãi suất là bao nhiêu phần trăm 1 tháng?
Đáp án:Vốn 2 triệu đồng 1 tháng sẽ có lãi là 11200 đồng
Vậy lãi suất 1 tháng là:
Vậy lãi suất là 0,56%
Bài 166 (trang 65 SGK Toán 6 tập 2): Học kì I số học sinh giỏi của lớp 6D là 2/7 số học sinh còn lại trong lớp. Sang học kỳ II số học sinh giỏi đã tăng thêm 8 bạn (tổng số học sinh không thay đổi) nên số học sinh giỏi chiếm 2/3 số học sinh của cả lớp. Hỏi trong học kỳ I lớp 6D có tất cả bao nhiêu học sinh giỏi?
Đáp án:Gọi số học sinh của lớp 6D là a.
+ Học kì I:
Số học sinh giỏi bằng 2/7 số học sinh còn lại của lớp.
--> số học sinh còn lại bằng 7/2 số học sinh giỏi.
Số học sinh của cả lớp = số học sinh giỏi + số học sinh còn lại
Vì vậy a = số HSG + 7/2 số HSG = (1+7/2) số HSG = 9/2 số học sinh giỏi.
Suy ra số học sinh giỏi = 2/9. a
+ Học kì II tương tự như học kì I ta có được:
Số học sinh giỏi = 2/5. a
+ Số học sinh giỏi kì II hơn số học sinh giỏi kì I là:
Mà theo đề bài: số học sinh giỏi kì II hơn số học sinh giỏi kì I là 8 học sinh
+ Số học sinh giỏi của lớp 6D trong học kì I là:
Bài 167 (trang 65 SGK Toán 6 tập 2): Đố: Đố em dựng được 1 đề toán mà khi sử dụng máy tính bỏ túi người ta giải đã bấm liên tiếp như dưới đây:

Đáp án:
Bài toán là: 1 lớp có 50 học sinh. Kết quả xếp loại văn hóa vào cuối năm có số học sinh xếp loại giỏi, khá, trung bình và yếu lần lượt chiếm 30%, 40%, 22% và 8% số học sinh cả lớp. Tính số học sinh của từng loại.
Bài trước: Bài 17: Biểu đồ phần trăm (trang 61 Toán 6 Tập 2) Bài tiếp: Ôn tập cuối năm phần số học (trang 66 SGK Toán 6 tập 2)