Bài 3: Đường thẳng đi qua hai điểm (trang 108 Toán 6 Tập 1)
Trả lời câu hỏi Toán 6 Tập 1 Bài 3 trang 108: Nếu đường thẳng chứa 3 điểm A, B và C thì gọi tên đường thẳng đó như thế nào (h. 18)?
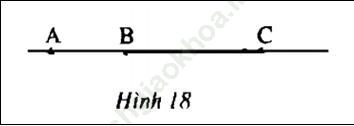
Đáp án:
Ta lấy tên 2 điểm 1 để gọi tên đường thẳng đó: đường thẳng BA, đường thẳng AB, đường thẳng BC, đường thẳng CB, đường thẳng AC và đường thẳng CA.
Bài 15 (trang 109 SGK Toán 6 Tập 1): Quan sát hình 21 và cho biết các nhận xét dưới đây đúng hay sai:
a) Có nhiều đường "không thẳng" đi qua 2 điểm là A và B.
b) Chỉ có 1 đường thẳng đi qua 2 điểm A và B.

Hình 21
Đáp án:
a) Đúng. 2 đường "không thẳng" chính là 2 đường cong như trên hình.
b) Đúng. Đó chính là đường thẳng AB.
Bài 16 (trang 109 SGK Toán 6 Tập 1): a) Tại sao không nói "2 điểm thẳng hàng"?
b) Cho 3 điểm A, B, C trên trang giấy và 1 thước thẳng (không chia khoảng). Phải kiểm tra như thế nào để có thể biết được 3 điểm đó có thẳng hàng hay không?
Đáp án:a) 2 điểm bất kì luôn luôn thẳng hàng (Luôn tồn tại 1 đường thẳng đi qua 2 điểm bất kì).
Do đó, ta không xét tính thẳng hàng của 2 điểm.
b) Qua 2 điểm A và B chỉ có 1 đường thẳng đi qua, gọi đó là đường thẳng d.
Nếu A, B và C thẳng hàng nếu chúng cùng nằm trên 1 đường thẳng
Do đó, để kiểm tra 3 điểm A, B và C thẳng hàng hay không thì ta chỉ cần sử dụng thước kẻ vẽ 1 đường thẳng đi qua hai điểm A và B sau đó xem đường thẳng đó có đi qua C hay không.

Bài 17 (trang 109 SGK Toán 6 Tập 1): Lấy 4 điểm A, B, C và D trong đó không có 3 điểm nào thẳng hàng. Kẻ các đường thẳng đi qua các cặp điểm. Kẻ được tất cả bao nhiêu đường thẳng? Đó là các đường thẳng nào?
Đáp án:Cứ qua 2 điểm ta lại vẽ được 1 đường thẳng.
Do đó ta có thể vẽ được những đường thẳng sau: AD, BC, BD, AB, AC, CD.
Có tất cả sáu đường thẳng.
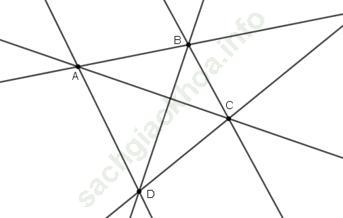
*Lưu ý: Đường thẳng BA chính là đường thẳng AB; đường thẳng CA chính là đường thẳng AC; … nên chỉ tính một lần.
Do đó, nếu bạn nào liệt kê những đường thẳng: BC, BD, CA, CB, CD, AB, AC, AD, BA, DA, DC DB, và kết luận rằng có 12 đường thẳng là kết luận sai.
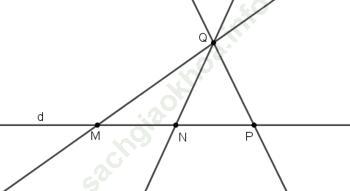
Bài 18 (trang 109 SGK Toán 6 Tập 1): Lấy 4 điểm M, N, P và Q trong đó có 3 điểm M, N và P thẳng hàng và điểm Q nằm ngoài đường thẳng trên. Kẻ các đường thẳng đi qua các cặp điểm. Có bao nhiêu đường thẳng (phân biệt). Viết tên những đường thẳng đó.
Đáp án:Tương tự như bài 17.
Cứ qua 2 điểm thì ta sẽ xác định được một đường thẳng.
Vậy qua 4 điểm M, N, P và Q ta sẽ xác định được 6 đường thẳng MQ, NP, NQ, PQ, MN, MP.
Tuy nhiên, 3 điểm M, N, P thẳng hàng nên những đường thẳng MN, NP và MP trùng nhau, ta chỉ tính một lần, gọi đó là đường thẳng d.
Vậy có bốn đường thẳng phân biệt đi qua những cặp điểm đã cho là: d (đi qua M, N, P); QM, QN và QP.
Bài 19 (trang 109 SGK Toán 6 Tập 1): Vẽ hình 22 vào vở rồi tìm điểm Z trên đường thẳng d1 và điểm T trên đường thẳng d2 sao cho Y, Z, T thẳng hàng và X, Z, T thẳng hàng.
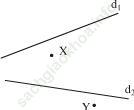
Hình 22
Đáp án:
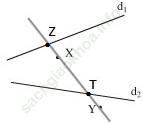
Vì Y, Z, T thẳng hàng và X, Z, T thẳng hàng nên cả bốn điểm này đều cùng nằm trên 1 đường thẳng XY.
Cách vẽ: Vẽ đường thẳng XY cắt d1 tại Z và cắt d2 tại T.
Bài 20 (trang 109 SGK Toán 6 Tập 1): Vẽ hình theo các cách diễn đạt dưới đây:
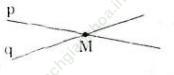
a) M là giao điểm của 2 đường thẳng q và p.
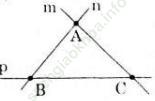
b) 2 đường thẳng m và n cắt nhau tại điểm A, đường thẳng p cắt đường thẳng n tại B và cắt đường thẳng m tại C.
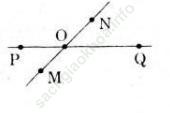
c) Đường thẳng PQ và đường thẳng MN cắt nhau tại O.
Đáp án:Các bạn có thể tham khảo cách vẽ hình dưới đây:
a)
b)
c)
Bài 21 (trang 110 SGK Toán 6 Tập 1): Xem hình 23 sau đó điền vào chỗ trống:
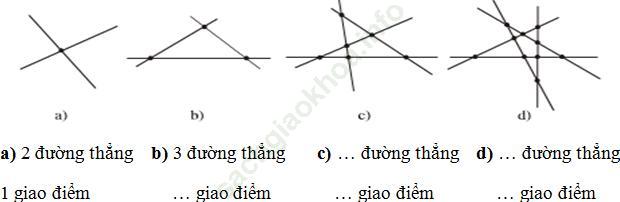
Hình 23
Đáp án:
Cách làm bài này là các bạn hãy đếm số đường thẳng cũng như số giao điểm sau đó điền vào chỗ trống:
a) 2 đường thẳng 1 giao điểm
b) 3 đường thẳng 3 giao điểm
c) 4 đường thẳng 6 giao điểm
d) 5 đường thẳng 10 giao điểm