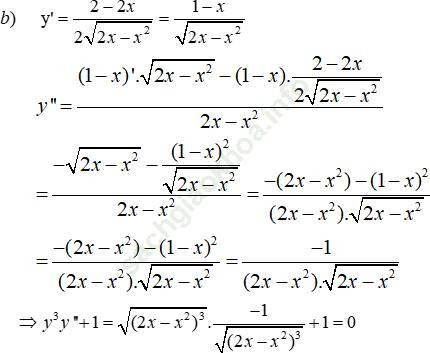Luyện tập (trang 219) - Giải BT Toán 11 nâng cao
Chương 5: Đạo hàm
Luyện tập (trang 219)
Bài 45 (trang 219 sgk Đại Số và Giải Tích 11 nâng cao): Tính vi phân của mỗi hàm số sau:
a) tan23x – cot3x2
Bài giải:
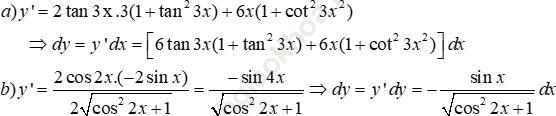
Bài 46 (trang 219 sgk Đại Số và Giải Tích 11 nâng cao): Dùng vi phân để tính gần đúng (làm tròn kết quả đến hàng phần nghìn):

Bài giải:
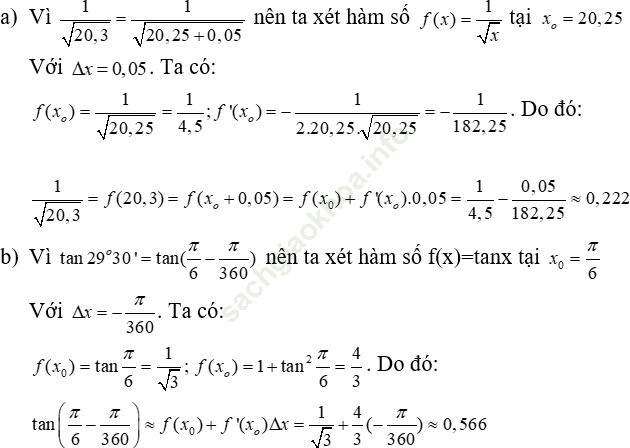
Bài 47 (trang 219 sgk Đại Số và Giải Tích 11 nâng cao):
a) Cho f (x) = tanx. Tính f(n)(x)với n = 1,2,3
b) Chứng minh rằng nếu: f (x) = sin2x thì f(4x)(x) = -24n -1cos2x (1)
Bài giải:a) f’ (x) = 1 + tan2x
f’’ (x) = 2tanx (1 + tan2x)
f(3)(x) = 2 (1 + tan2x) 2 + 4tan2x (1 + tan2x)
b) Với n = 1 ta có
f' (x) = sin2x
f’’ (x) = 2cos2x
f(3)(x) = -4sin2x
f(4)(x) = -8cos2x
Vậy (1) đúng với n = 1
Giả sử (1) đúng với n=k tức là: f(4k)(x) = -24k -1cos2x
Với n = k+1 ta có:
f(4k+1)(x) = (f4k(x)) = 24ksin2x
f(4k+2)(x) = 2f4k+1cos2x
f(4k+3)(x) = -2f4k+2sin2x
f(4k+4)(x) = -2f4k+3cos2x
Vậy (1) đúng với n = k+1 do đó (1) đúng với mọi n.
Bài 48 (trang 219 sgk Đại Số và Giải Tích 11 nâng cao): Chứng minh rằng:
a) Nếu y = Asin (ω t + φ) + Bcos (ω t + φ), trong đó A, B, ω và φ là những hằng số, thì y’’ + ω2y = 0Bài giải:
a) y = Asin (ω t + φ) + Bcos (ω t + φ)
y’ = Aω cos (ω t + φ) - Bω sin (ω t + φ)
y’’ = -Aω2 sin (ω t + φ) - Bω2 cos (ω t + φ)