Bài 1: Vectơ trong không gian. Sự đồng phẳng của các vectơ - Giải BT Toán 11 nâng cao
Chương III. Vectơ trong không gian. Quan hệ vuông góc
Bài 1: Vectơ trong không gian. Sự đồng phẳng của các vectơ
Bài 1 (trang 91 sgk Hình học 11 nâng cao): Ba vectơ ![]()
a) Có một véc tơ trong ba véc tơ đó bằng ![]()
b) Có hai trong ba véc tơ đó cùng phương.
Bài giải:
Bài 2 (trang 91 sgk Hình học 11 nâng cao): Cho hình chóp S. ABCD

Bài giải:
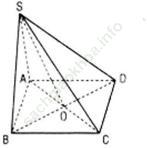

Điều này chứng tỏ O, M, N thẳng hàng.
Mặt khác: M thuộc AC, N thuộc BD và O là giao điểm của AC và BD nên O, M, N thẳng hàng chỉ xảy ra khi O ≡ M ≡ N, tức O là trung điểm của AC và BD, hay ABCD là hình bình hành.
Bài 3 (trang 91 sgk Hình học 11 nâng cao): Cho hình lăng trụ tam giác ABC. A’B’C’. Gọi G và G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’, I là giao điểm của 2 đường thẳng AB’ và A’B, chứng minh rằng các đường thẳng GI và CG’ song song với nhau
Bài giải: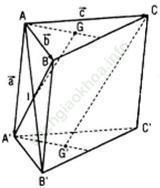
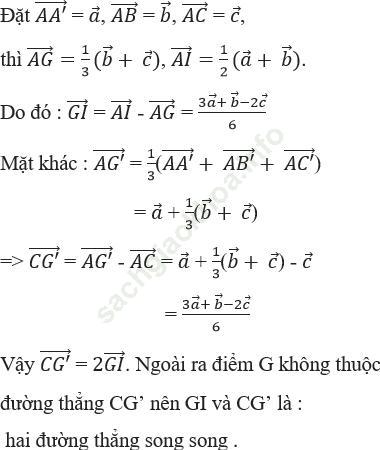
Bài 4 (trang 91 sgk Hình học 11 nâng cao): Cho hình hộp ABCD. A’B’C’D’. Gọi M và N lần lượt là trung điểm của CD và DD’; G và G’ lần lượt là trọng tâm của các tứ diện A’D’MN và BCC’D’. Chứng minh rằng đường thẳng GG’ và mặt phẳng (ABB’A’) song song với nhau.
Bài giải: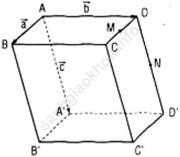

Bài 5 (trang 91 sgk Hình học 11 nâng cao): Trong không gian cho tam giác ABC
a) Chứng minh rằng nếu điểm M thuộc mặt phẩng (ABC) thì có 3 số x, y, z mà x + y + z = 1 sao cho:
b) Ngược lại, nếu có một điểm O trong không gian sao cho:
Trong đó x + y + z = 1 thì điểm M thuộc mp (ABC)
Bài giải:

Bài 6 (trang 91 sgk Hình học 11 nâng cao): Cho hình chóp S. ABCD lấy các điểm A’B’C’ lần lượt thuộc các tia SA, SA, SC sao cho SA = aSA’, SB = bSB’, SC = cSC’. Trong đó a, b, c là các số thay đổi. Chứng minh rằng mặt phẳng (A’B’C’) đi qua trọng tâm của tam giác ABC khi và chỉ khi a + b + c = 3.
Bài giải: