Bài 4: Cấp số nhân - Giải BT Toán 11 nâng cao

Chương 3: Dãy số. Cấp số cộng và cấp số nhân Bài 4: Cấp số nhân

Bài 29 (trang 120 sgk Đại Số và Giải Tích 11 nâng cao): Trong các dãy số dưới đây, dãy số nào là cấp số nhân? Hãy xác định công bội của cấp số nhân đó?

a) Dãy số 1, -2,4, -8,16, -32,64;

b) Dãy số (u_n với u_n = n. 6 ^{n + 1}

c) Dãy số (v_n) với v_n = (-1) ⁿ.3 ²ⁿ;

d) Dãy số (x_n) với x_n = (-4)^{2n + 1}

Bài giải:

a) Dãy số đã cho là một cấp số nhân với công bội: q = -2

b)

Suy ra (u_n) không phải là cấp số nhân.

c)

Suy ra (v_n) là một cấp số nhân với công bội q = -9

d)

Suy ra (x_n) là một cấp số nhân với công bội q = 16

Bài 30 (trang 120 sgk Đại Số và Giải Tích 11 nâng cao): Trong mỗi câu sau, hãy đánh dấu “X” vào phần kết luận mà em cho là đúng:

a) Mỗi cấp số nhân có số hạng đầu dương và công bội 0 < q < 1, là một dãy số

□ Tăng

□ Giảm

□ Không tăng cũng không giảm

b) Mỗi cấp số nhân có số hạng đàu dương và công bội q > 1 là một dãy số

□ Tăng

□ Giảm

□ Không tăng cũng không giảm

Bài giải:

a) Giảm

b) Tăng

Bài 31 (trang 121 sgk Đại Số và Giải Tích 11 nâng cao): Cho cấp số nhân (u_n) có công bội q < 0. Biết u₂ = 4 vàu₄ = 9, hãy tìm u₁

Bài giải: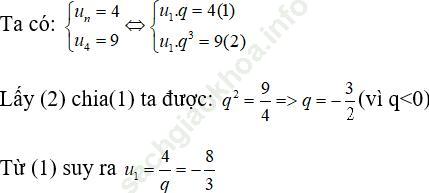

Bài 32 (trang 121 sgk Đại Số và Giải Tích 11 nâng cao): Một cấp số nhân có năm số hạng mà hai số hạng đầu tiên là các số dương. Tích của số hạng đầu và số hạng thứ ba bằng 1, tích của số hạng thứ 3 và số hạng cuối bằng 1/16. Hãy tìm cấp số nhân đó.

Bài giải:

Với mỗi n ∈ {1,2,3,4,5}, kí hiệu u_n là số hạng thứ n của cấp số nhân đã cho.

Vì u₁ > 0, u₂ > 0 nên cấp số nhân (u_n) có công bôi q > 0,

Do đó u_n > 0 Ɐn ∈ {1,2,3,4,5}. Từ đó:

Bài 33 (trang 121 sgk Đại Số và Giải Tích 11 nâng cao): Cho cấp số nhân (u_n) với công bội q ≠ 0 và u₁ ≠ 0. Cho các số nguyên dương m và k, với m ≥ k. Chứng minh rằng u_m = u_k.q^{m – k}

a) Tìm công bội q của cấp số nhân (u_n) có u₄ = 2 và u₇ = -686

b) Hỏi có tồn tại hay không một cấp số nhân (u_n) mà u₂ = 5 và u₂₂ = -2000?

Bài giải:

Bài 34 (trang 121 sgk Đại Số và Giải Tích 11 nâng cao): Hãy tìm số hạng tổng quát của cấp số nhân (u _n), biết rằng u ₃ = -5 và u ₆ = 135

Bài giải:

Gọi q là công bội của cấp số nhân đã cho. Theo kết quả của bài tập 33, ta có:

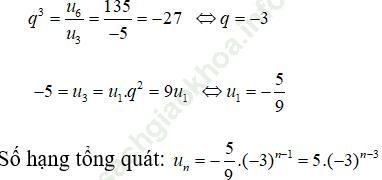
Bài 35 (trang 121 sgk Đại Số và Giải Tích 11 nâng cao): Chu kì bán rã của nguyên tố phóng xạ poloni 210 là 138 ngày (nghĩa là sau 138 ngày khối lượng của nguyên tố đó chỉ còn 1 nửa). Tính (chính xác đến phần hàng trăm) khối lượng còn lại của 20 gam poloni 210 sau 7314 ngày (khoảng 20 năm).

Bài giải:

Kí hiệu: u_n (gam) là khối lượng còn lại của 20 gam poloni sau n chu kỳ bán rã.

Ta có 7314 ngày gòm 53 (=7314: 138) chu kì bán rã.

Như thế, theo đề bài, ta cần tính u₅₃.

Từ giả thiết của bài toán suy ra dãy số u_n là một cấp số nhân với số hạng đầu u₁ = 20: 2 = 10 và công bội q = 1/2. Do đó:

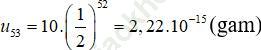
Bài 36 (trang 121 sgk Đại Số và Giải Tích 11 nâng cao): Tính các tổng sau:

a) Tổng tất cả các số hạng của một cấp số nhân, biết rằng số hạng đầu bằng 18, số hạng thứ 2 bằng 54 và số hạng cuối cùng bằng 39366.

b) Tổng tất cả các số hạng của một cấp số nhân, biết rằng số hạng đầu bằng 1/256, số hạng thứ 2 bằng -1/512 và số hạng cuối cùng bằng 1/1048576.

Bài giải:

a)

b)

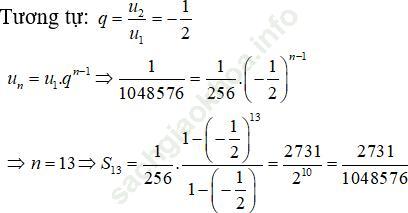
Bài 37 (trang 121 sgk Đại Số và Giải Tích 11 nâng cao): Số đo bốn góc của một tứ giác lồi lập thành một cấp số nhân. Hãy tìm bốn góc đó, biết rằng số đo của góc lớn nhất gấp 8 lần số đo của góc nhỏ nhất.

Bài giải:

Kí hiệu A, B, C, D là số đo bốn góc (tính theo đơn vị độ) của tứ giác lồi đã cho. Không mất tổng quát, giả sử. Khi đó, từ giả thiết của bài toán ta có D=8A, và A, B, C, D theo thứ tự đó lập thành một cấp số nhân.

Gọi q là công bội của cấp số nhân đó, ta có:

8A = D = A. q³ ⇒ q = 2

Do đó: 360 = A + B + C + D = A. (1 – 2⁴)/ (1 – 2) = 15A ⇒ A = 24 (độ)

Suy ra B = A. 2 = 48 (độ), C = A. 2² = 96 và D = A. 2³ = 192 (độ)

Bài trước: Bài 3: Cấp số cộng - Giải BT Toán 11 nâng cao Bài tiếp: Luyện tập (trang 121) - Giải BT Toán 11 nâng cao