Luyện tập (trang 175-176) - Giải BT Toán 11 nâng cao
Chương 4: Giới hạn B. Giới hạn của hàm số
Luyện tập (trang 175-176)
Bài 50 (trang 175 sgk Đại Số và Giải Tích 11 nâng cao): Chứng minh rằng:
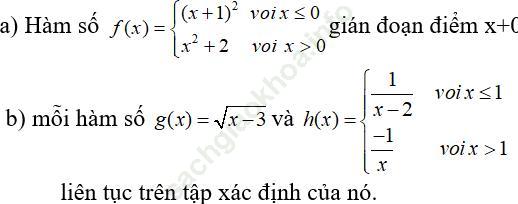
Bài giải:

Bài 51 (trang 175 sgk Đại Số và Giải Tích 11 nâng cao): Giải thích tại sao:
a) Hàm số f (x) = x2sinx – 2cos2x + 3 liên tục trên R
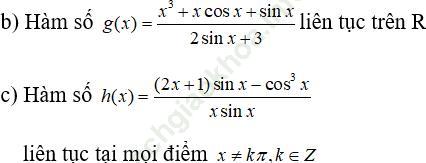
Bài giải:

Bài 52 (trang 176 sgk Đại Số và Giải Tích 11 nâng cao): Chứng minh rằng hàm số
Bài giải:
Tập xác định D = R\ {2}
Với mọi xo ≠ 2, ta có:
Suy ra f liên tục tại mọi xo ≠ 2 nên f liên tục trên tập xác định.
Bài 53 (trang 176 sgk Đại Số và Giải Tích 11 nâng cao): Chứng minh rằng phương trình x3 + x + 1 = 0 có ít nhất một nghiệm âm lớn hơn -1.
Bài giải:Hàm số f (x) = x3 + x + 1 = 0 liên tục trên đoạn [-1; 0] có f (-1) = -1 và f (0) = 1
Vì f (-1)f (0) < 0 nên theo hệ quả của định lí về giá trị trung gian của hàm liên tục, tồn tại ít nhất một điểm c ∈ (-1; 0) sao cho f (c) = 0. Số c là nghiệm âm lớn hơn -1 của phương trình đã cho.
Bài 54 (trang 176 sgk Đại Số và Giải Tích 11 nâng cao): Cho hàm số:
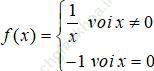
a) Chứng tỏ rằng f (-1)f (2) < 0
b) Chứng tỏ rằng phương trình f (x)=0 không có nghiệm thuộc khoảng (-1; 2)
c) Điều khẳng định trong b) có mâu thuẫn với định lí về giá trị trung gian của hàm số liên tục hay không?
Bài giải:a) Ta có: f (-1)=-1; f (2)=1/2
⇒ f (-1).f (2) < 0
b) Vì f (0) ≠ 0với mọi x ∈ R nên phương trình f (x)=0 không có nghiệm.
c) Điều khẳng định trong b) không mâu thuẫn với định lí về giá trị trung gian của hàm số liên tục vì hàm số f gián đoạn tại điểm x = 0 ∈ [-1; 2]