Luyện tập (trang 212-113) - Giải BT Toán 11 nâng cao
Chương 5: Đạo hàm
Luyện tập (trang 212-113)
Bài 33 (trang 212 sgk Đại Số và Giải Tích 11 nâng cao): Tìm đạo hàm của mỗi hàm số sau:
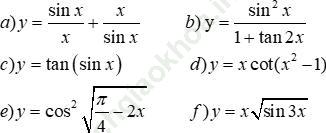
Bài giải:

Bài 34 (trang 212 sgk Đại Số và Giải Tích 11 nâng cao):
Bài giải:
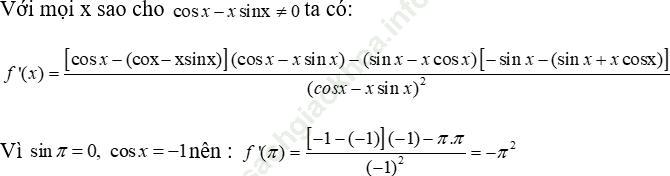
Bài 35 (trang 212 sgk Đại Số và Giải Tích 11 nâng cao): Giải phương trình y’ = 0 trong các trường hợp sau:
a) y = sin2x – 2cosx
b) y = 3sin2x + 4cos2x + 10x
c) y = cos2x + sinx
d) y = tanx + cotx
Bài giải:
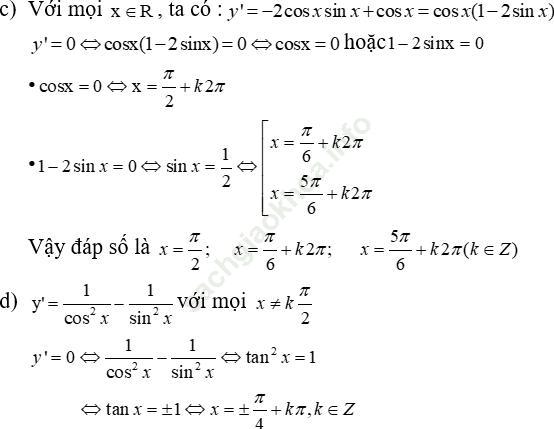
Bài 36 (trang 212 sgk Đại Số và Giải Tích 11 nâng cao): Cho hàm số:
f (x) = 2 cos2x (4x – 1).
Chứng minh rằng với mọi x ta có |f’ (x) ≤ 8|. Tìm các giá trị của x để đẳng thức xảy ra.
Bài giải:Với mọi x, ta có:
f' (x) = 2.2cos (4x – 1)[-sin (4x – 1)]4 = -8 sin2 (4x – 1)
Suy ra f’ (x) = 8|sin2 (4x – 1)| ≤ 8
Dấu đẳng thức xảy ra khi và chỉ khi:
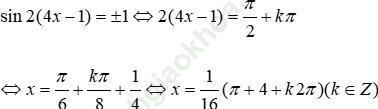
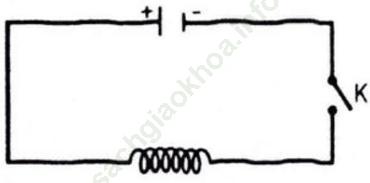
Bài 37 (trang 212 sgk Đại Số và Giải Tích 11 nâng cao): Cho mạch điện như hình vẽ. Lúc đầu tụ điện có điện tích Qo. Khi đóng khóa K, tụ điện phóng điện qua cuộn dây; điện tích q của tụ điện phụ thuộc vào thời gian t theo công thức q (t) = Qosinω t, trong đó, ω là tốc độ góc. Biết rằng cường độ I (t) của dòng điện tại thời điểm t được tính theo công thức I (t) = q’ (t).
Cho biết Qo = 10-8C và ω = 106π rad/s. Hãy tính cường độ của dòng điện tại thời điểm t = 6s (tính chính xác đến 10-5mA).
Bài giải:
Cường độ dòng điện tại thời điểm t là:
I (t) = q’ (t) = Qocosω t
Khi Qo = 10-8C và ω = 106π rad/s thì cường độ dòng điện tại thời điểm t=6s là:
Bài 38 (trang 213 sgk Đại Số và Giải Tích 11 nâng cao): Cho hàm số:
y = cos2x + msinx (m là tham số) có đồ thị là (C).
Tìm m trong mỗi trường hợp sau:
a) Tiếp tuyến của (C) tại điểm với hoành độ x = π có hệ số góc bằng 1.
b) Hai tiếp tuyến của (C) tại các điểm có hoành độ x = -π /4 và x = π /3 song song với nhau hoặc trùng với nhau.
Bài giải:Đặt f (x) = cos2x + msinx, ta có:
f’ (x) = -2sin2x + mcosx
a) Hệ số góc tiếp tuyến của (C) tại điểm có hoành độ x = π là:
f’ (π) = -2sin2π + mcosπ
Vậy f’ (π) = 1 ⇔ m = -1
