Câu hỏi và bài tập ôn tập cuối năm - Giải BT Toán 11 nâng cao
Câu hỏi và bài tập ôn tập cuối năm
Bài 1 (trang 223 sgk Đại Số và Giải Tích 11 nâng cao):
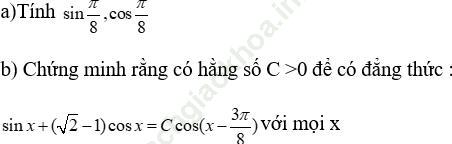
Bài giải:

Bài 2 (trang 223 sgk Đại Số và Giải Tích 11 nâng cao): Giải Phương trình:
tan x = cot 2x
Biểu diễn các nghiệm trên đường tròn lượng giác?
Bài giải: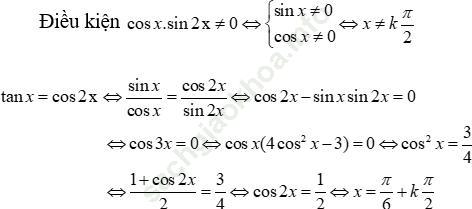
Bài 3 (trang 223 sgk Đại Số và Giải Tích 11 nâng cao):
a) Tìm giá trị nhỏ nhất của biểu thức P (x) = (sinx + cosx)3
Bài 4 (trang 223 sgk Đại Số và Giải Tích 11 nâng cao): Giải các phương trình.
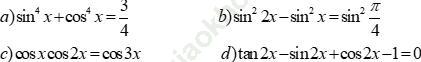
Bài giải:
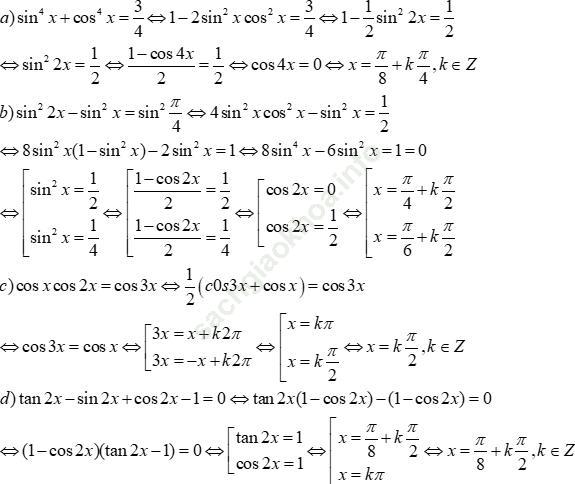
Bài 5 (trang 224 sgk Đại Số và Giải Tích 11 nâng cao): Giải các phương trình sau:
Bài giải:


Bài 6 (trang 224 sgk Đại Số và Giải Tích 11 nâng cao): Giải các phương trình:
Bài giải:
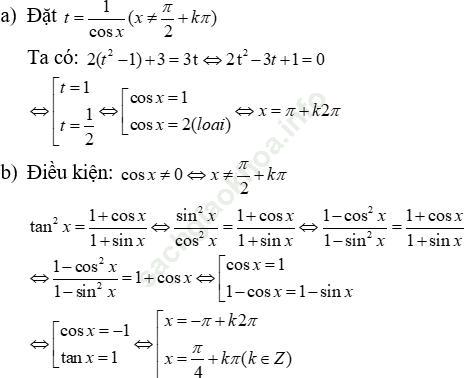
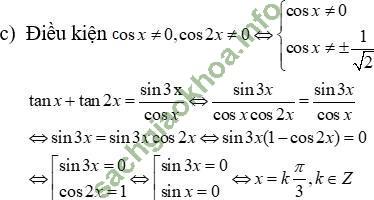
Bài 7 (trang 224 sgk Đại Số và Giải Tích 11 nâng cao): Một đoàn tàu nhỏ có 3 toa khách đỗ ở sân ga. Có 3 hành khách bước lên tàu. Hỏi:
a) Có bao nhiêu khả năng trong đó 3 hành khách lên 3 toa khác nhau?
b) Có bao nhiêu khả năng trong đó 2 hành khách cùng lên một toa, còn hành khách thứ ba thì lên toa khác?
Bài giải:a) Mỗi cách xếp 3 người vào 3 toa, mỗi toa môt người là một hoắn vị của tập hợp 3 hành khách. Vạy có 3! = 6 khả năng.
b) Có C32 = 3 cách chọn hai hành khách đi chung toa. Với mỗi cách ấy lại có 3 cách chọn toa tàu cho họ. Vậy có 3.3 = 9 cách chọn hai hành khách và toa tàu cho họ đi chung. Mỗi cách ấy, hành khách thứ ba có thể chọn một trong hai toa tàu còn lại. Áp dụng quy tắc nhân, ta có 9.2 = 18 khả năng có thể xảy ra.
Bài 8 (trang 224 sgk Đại Số và Giải Tích 11 nâng cao): Cho tập hợp A= {1,2, …, n} với n ∈ N, n > 1. Hỏi có bao nhiêu cặp (x; y) với x ∈ A, y ∈ A và x > y?
Bài giải:Với hai phần tử x và y của A sao cho x > y, ta chỉ lập được một cặp duy nhất (x; y) thỏa mãn đề bài. Do đó mỗi cặp như vậy có thể xem là một tổ hợp chập 2 của n phần tử.
Bài 9 (trang 224 sgk Đại Số và Giải Tích 11 nâng cao): Một túi chứa 16 viên bi, trong đó có 7 viên bi trắng, 6 viên bi đen và 3 viên bi đỏ.
a) Lấy ngẫu nhiên 2 viên bi trong túi
+ Tính xác suất để được 2 viên bi đen.
+ Tính xác suất để được 1 viên bi đen và 1 viên bi trắng.
b) Lấy ngẫu nhiên 3 viên bi trắng trong túi
+ Tính xác suất để được 3 viên bi đỏ
+ Tính xác suất để được 3 viên bi với 3 màu khác nhau.
Bài giải:
Bài 10 (trang 224 sgk Đại Số và Giải Tích 11 nâng cao): Gọi X là biến ngẫu nhiên chỉ số điểm mà một vận động viên bắn cung nhận được khi bắn một lần. Giả sử X có bảng phân bố xác suất như sau:
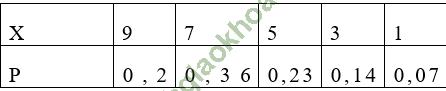
a) Tính điểm trung bình khi vận động viên đó bắn một lần
b) Tính điểm trung bình khi vận động viên đó bắn 48 lần.
Bài giải:a) Ta có E (x) = 9.0,2+7.0,36+5.0,23+3.0,14+1.0,07 = 5,96
b) Điểm trung bình khi vận động viên đó bắn 48 lần là: 48.5,96 = 286,08
Bài 11 (trang 225 sgk Đại Số và Giải Tích 11 nâng cao):


Bài 12 (trang 225 sgk Đại Số và Giải Tích 11 nâng cao): Cho dãy số (un) xác định bởi:

Bài giải:
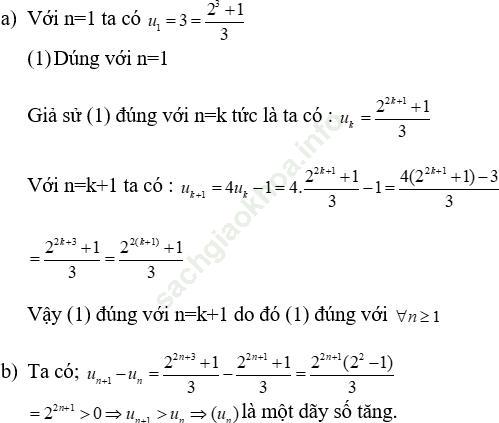
Bài 13 (trang 225 sgk Đại Số và Giải Tích 11 nâng cao): Cho dãy số (un) xác định bởi:
u1 = 5 và un = un-1 - 2 với mọi n ≥ 2
a) Hãy tìm số hạng tổng quát của dãy số (un)
b) Hãy tính tổng 100 số hạng đầu tiên của dãy số (un)
Bài giải:a) Ta có: un+1 - un = - 2, Ɐn ≥ 1
b) Suy ra (un)là một cấp số cộng có số hạng đầu là u1 = 5 và công sai d=-2. Do đó: un = u1 + (n -1)d = 5 + (n – 1)(-2) = -2n + 7
Bài 14 (trang 225 sgk Đại Số và Giải Tích 11 nâng cao): Cho dãy số (un)xác định bởi:
u1 = 2 và un = 3un-1 với mọi n ≥ 2
a) Hãy tìm số hạng tổng quát của dãy số (un)
b) Hãy tính tổng 10 số hạng đầu tiên của dãy số (un)
Bài giải:
Bài 15 (trang 225 sgk Đại Số và Giải Tích 11 nâng cao): Các số x – y, x + y và 3x – 3y theo thứ tự lập thành một cấp số cộng và đồng thời các số x – 2, y + 2 và 2x + 3y theo thứ tự lập thành một cấp số nhân. Hãy tìm x và y
Bài giải: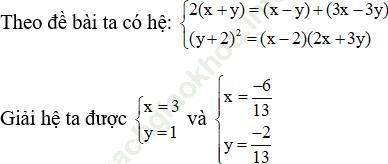
Bài 16 (trang 226 sgk Đại Số và Giải Tích 11 nâng cao): Tính giới hạn của các dãy số sau:
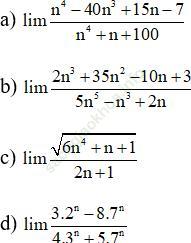
Bài giải:
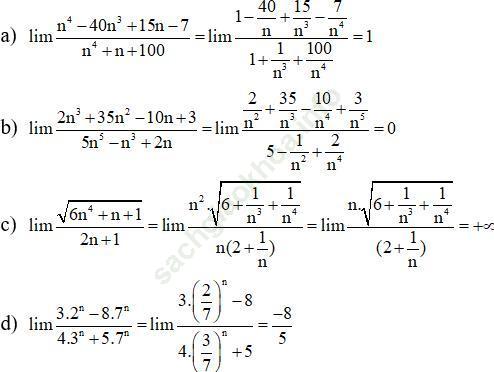
Bài 17 (trang 226 sgk Đại Số và Giải Tích 11 nâng cao): Tính các giới hạn sau:
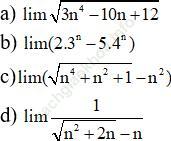
Bài giải:
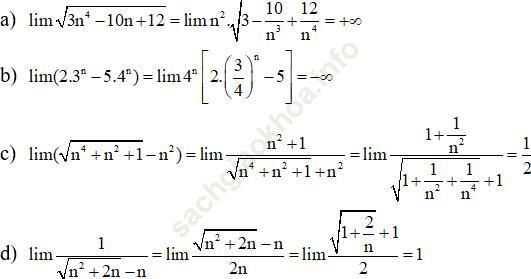
Bài 18 (trang 226 sgk Đại Số và Giải Tích 11 nâng cao): Tìm số hạng đầu và công bội của một cấp số nhân lùi vô hạn biết rằng số hạng thứ hai là 12/5 và tổng của cấp số nhân này là 15.
Bài giải:Gọi u1, q là số hạng đầu và công bội của cấp số nhân (|q| < 1). Theo đề bài ta có:
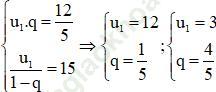
Bài 19 (trang 226 sgk Đại Số và Giải Tích 11 nâng cao): Tính các giới hạn sau:
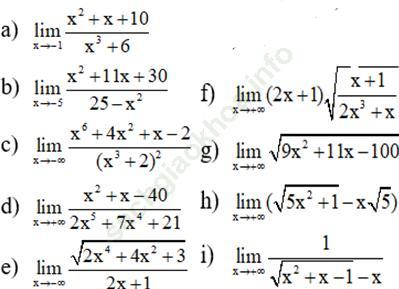
Bài giải:
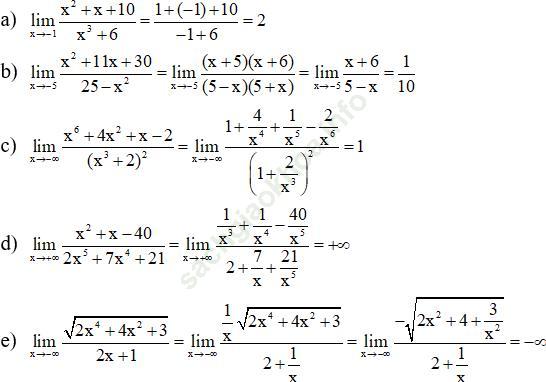
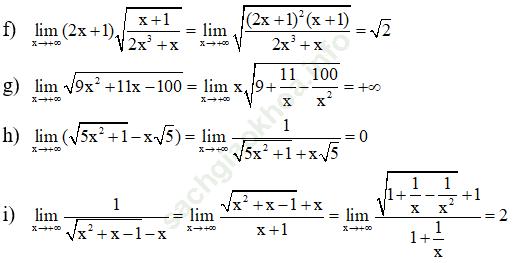
Bài 20 (trang 226 sgk Đại Số và Giải Tích 11 nâng cao): Chứng minh rằng phương trình: x3 + ax2 + bx + c = 0 luôn có ít nhất một nghiệm.
Bài giải:
Bài 21 (trang 226 sgk Đại Số và Giải Tích 11 nâng cao): Tìm đạo hàm của các hàm số sau:
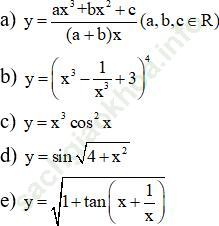
Bài giải:
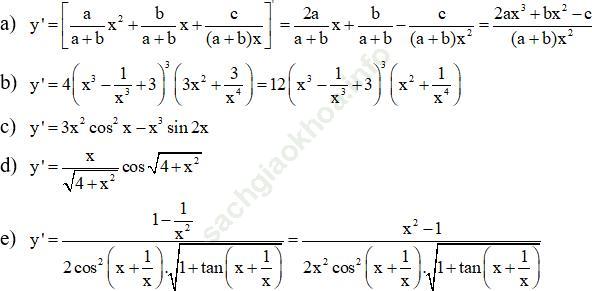
Bài 22 (trang 227 sgk Đại Số và Giải Tích 11 nâng cao): Cho hàm số:
y = mx3 + x2 + x – 5. Tìm m để:
a) y’ bằng bình phương của một nhị thức bậc nhất
b) y’ có hai nghiệm trái dấu
c) y’ > 0 với mọi x.
Bài giải:
Bài 23 (trang 227 sgk Đại Số và Giải Tích 11 nâng cao): Giải các phương trình sau:
b) y’=0 với y = sin3x – 2cos3x – 3x + 4
Bài giải:
Bài 24 (trang 227 sgk Đại Số và Giải Tích 11 nâng cao): Cho hyperbol (H) xác định bởi phương trình y = 1/x
a) Tìm phương trình tiếp tuyến (T) của (H) tại điểm A có hoành độ a (với a khác 0)
b) Giả sử (T) cắt trục Ox tại điểm I và trục Oy tại điểm J. Chứng minh rằng A là trung điểm của đoạn IJ. Từ đó suy ra cách vẽ tiếp tuyến (T)
c) Chứng minh rằng diện tích tam giác OIJ không phụ thuộc vào vị trí của điểm A
Bài giải:
Bài 25 (trang 227 sgk Đại Số và Giải Tích 11 nâng cao): Một điểm M chuyển động trên parabol y =- x2 + 17x – 66 theo hướng tăng của x. Một người quan sát đứng ở vị trí P (2; 0).
Hãy xác định các giá trị của hoành độ điểm M để người quan sát có thể nhìn thấy được điểm M.
Bài giải:
+) Người quan sát thấy được điểm M nếu M thuộc phần parabol nằm trong góc tạo bởi hai tiếp tuyến của parabol đi qua P (2; 0). Điều đó tương đương với bất đẳng thức kép x1 ≤ m ≤ x2; trong đó m là hoành độ của điểm M, x1 và x2 là hoành độ hai tiếp điểm. Ta cần xác định x1 và x2.
+) Phương trình đường thẳng (d) đi qua P (2; 0) với hệ số góc bằng k là:
y=k (x – 2) + 0 hay y = kx – 2k
Để (d) là tiếp tuyến của parabol y = −x2+17x− 66 thì hệ sau phải có nghiệm:

(x1 và x2 chính là hai hoành độ tiếp điểm của hai tiếp tuyến kẻ từ P (2; 0) đến parabol đã cho).
Vậy người quan sát có thể nhìn được các điểm M thuộc parabol đã cho, nếu hoành độ điểm M thuộc đoạn [-4; 8].