Bài 1: Các hàm số lượng giác - Giải BT Toán 11 nâng cao
Chương 1: Hàm số lượng giác và phương trình lượng giác
Bài 1: Các hàm số lượng giác
Bài 1 (trang 14 sgk Đại Số và Giải Tích 11 nâng cao): Tìm tập xác định của các hàm số sau:

Bài giải:
a) Vì -1 ≤ sinx ≤ 1 nên 3 - sinx > 0 với mọi x nên tập xác định của hàm số là D = R.
b) y = (1 - cosx)/sinx xác định khi và chỉ khi sinx ≠ 0
⇔ x ≠ kπ, k ∈ Z.
Vậy tập xác định D = R\ {kπ |k ∈ Z}
c) Vì 1 - sinx ≥ 0 và 1 + cosx ≥ 0 nên hàm số xác định khi và chỉ khi
cosx ≠ -1 ⇔ x ≠ π + k2π, k ∈ Z.
Vậy tập xác định D = R\ {π + k2π |k ∈ Z}
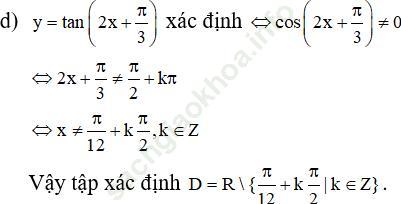
Bài 2 (trang 14 sgk Đại Số và Giải Tích 11 nâng cao): Xét tính chẵn – lẻ của các hàm số sau:
a) y = -2sinx
b) y = 3sinx - 2
c) y = sinx - cosx
d) y = sinxcos2x + tanx
Bài giải:a) f (x) = -2sinx
Tập xác định D = R, ta có f (-x) = -2sin (-x) = 2sinx = -f (x), ∀ x ∈ R
Vậy y = -2sinx là hàm số lẻ.
b)
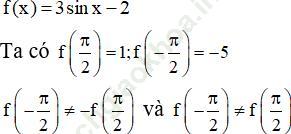
Nên hàm số y = 3sinx - 2 không phải là hàm số chẵn cũng không phải là hàm số lẻ.
c)
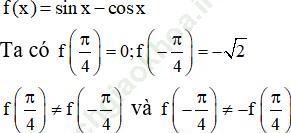
Nên y = sinx - cosx không phải là hàm số chẵn cũng không phải là hàm số lẻ.
d)
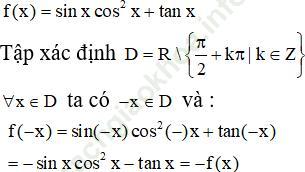
Nên hàm số đã cho là hàm số lẻ.
Bài 3 (trang 14 sgk Đại Số và Giải Tích 11 nâng cao): Tìm giá trị lớn nhất và giá trị nhỏ nhất của mỗi hàm số sau:
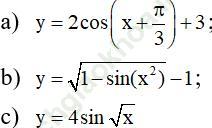
Bài giải:
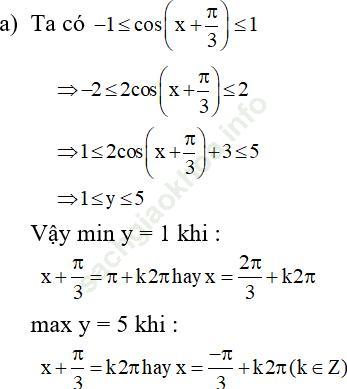
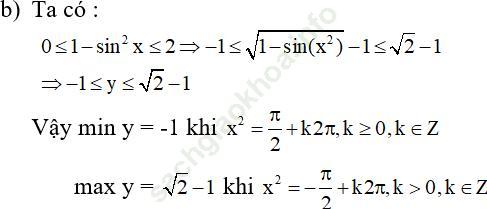
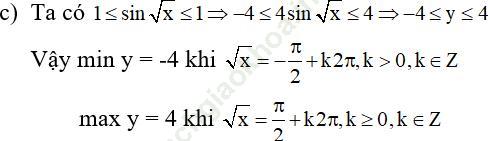
Bài 4 (trang 14 sgk Đại Số và Giải Tích 11 nâng cao): Cho các hàm số f (x) = sin x, g (x) = cos x, h (x) = tan x và các khoảng
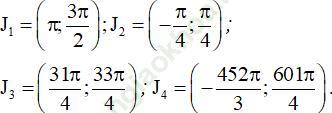
Hỏi hàm số nào trong ba hàm số đồng biến trên khoảng J1? Trên khoảng J2? Trên khoảng J3? Trên khoảng J4? (Trả lời bằng cách lập bảng).
Bài giải: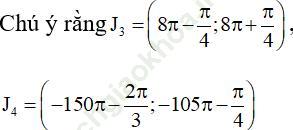
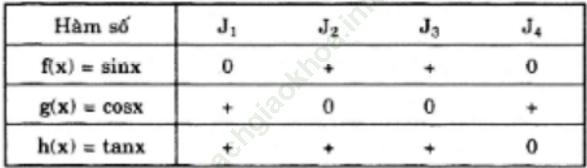
Ta có bảng sau, trong đó dấu “+” có nghĩa đồng biến, dấu “0” có nghĩa không đồng biến:
Bài 5 (trang 14 sgk Đại Số và Giải Tích 11 nâng cao): Trong các khẳng định sau, khẳng định nào đúng? Khẳng định nào sai? Giải thích vì sao?
a) Trên mỗi khoảng mà hàm số y = sin x đồng biến thì hàm số y = cos x nghịch biến.
b) Trên mỗi khoảng mà hàm số y = sin2x thì hàm số y = cos2x nghịch biến.
Bài giải:a) Sai vì trên khoảng (-π /2; π /2) hàm số y = sin x đồng biến nhưng hàm số y = cosx không nghịch biến.
b) Đúng do sin2x + cos2x = 1
Giả sử y = sin2x đồng biến trên khoảng I, khi đó với x1, x2 ∈ I và x1 < x2 thì
sin2x1 < sin2x2
⇒ 1 - sin2x1 > 1 - sin2x2 ⇒ cos2x1 > cos2x1
⇒ y = cos2x nghịch biến trên I.
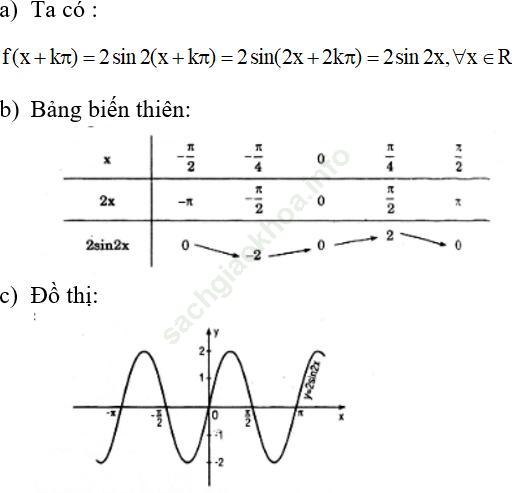
Bài 6 (trang 15 sgk Đại Số và Giải Tích 11 nâng cao): Cho hàm số y = f (x) = 2sin2x
a) Chứng minh rằng với số nguyên k tùy ý, luôn có f (x + kπ) = f (x), ∀ x
b) Lập bảng biến thiên của hàm số y = 2sin2x trên đoạn [-π /2; π /2]
c) Vẽ đồ thị hàm số y = 2sin2x
Bài giải: