Bài 3: Đạo hàm của các hàm số lượng giác - Giải BT Toán 11 nâng cao
Chương 5: Đạo hàm
Bài 3: Đạo hàm của các hàm số lượng giác
Bài 28 (trang 211 sgk Đại Số và Giải Tích 11 nâng cao): Tìm các giới hạn sau:
Bài giải:
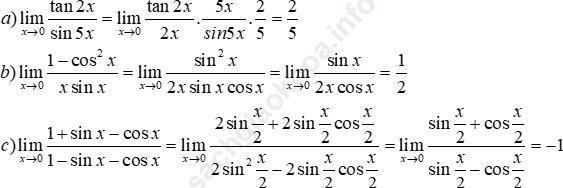
Bài 29 (trang 211 sgk Đại Số và Giải Tích 11 nâng cao): Tính đạo hàm của các hàm số sau:
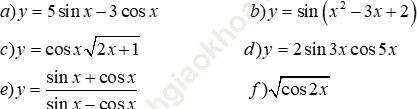
Bài giải:
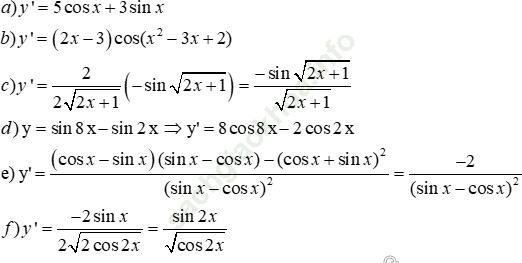
Bài 30 (trang 211 sgk Đại Số và Giải Tích 11 nâng cao): Chứng minh rằng hàm số:
y = sin6x + cos6x + 3sin2xcos2x có đạo hàm bằng 0.
Bài giải:Ta có: y = (sin2x + cos2x)(sin4x - sin2xcos2x - cos4x) + 3sin2xcos2x
= sin4 + 2sin2xcos2x + cos4x = (sin2x + cos2x) 2 = 1 ⇒ y’ = 0
Bài 31 (trang 212 sgk Đại Số và Giải Tích 11 nâng cao): Tìm đạo hàm của các hàm số sau:
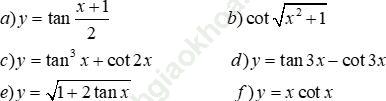
Bài giải:
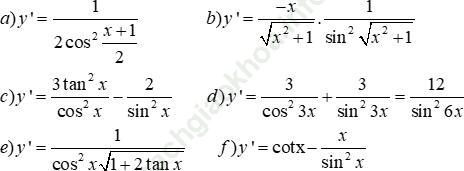
Bài 32 (trang 212 sgk Đại Số và Giải Tích 11 nâng cao): Chứng minh rằng:
a) Hàm số y = tanx thỏa mãn hệ thức y’ – y2 - 1 = 0
b) Hàm số y = cot2x thỏa mãn hệ thức y’ + 2y2 + 2 = 0
Bài giải:a) y’ = 1 + tan2x. Do đó y’ - y2 - 1 = (1 + tan2x) - tan2x – 1 = 0
b) y’ = -2 (1 + cot22x). Do đó y’ + 2y2 + 2 = -2 (1 + cot22x) + 2cot22x + 2 = 0