Bài 1: Phương pháp quy nạp toán học - Giải BT Toán 11 nâng cao

Bài 2 (trang 100 sgk Đại Số và Giải Tích 11 nâng cao): Chứng minh rằng với mọi số nguyên dương n ta luôn có đẳng thức sau:

Vậy (1) đúng với n=k+1 do đó (1) đúng với mọi n nguyên dương.

Bài 3 (trang 100 sgk Đại Số và Giải Tích 11 nâng cao): Chứng minh rằng với mọi số nguyên dương n ta luôn có bất đẳng thức sau:

Điều này luôn đúng. Suy ra (*) đúng. Từ đó suy ra điều phải chứng minh.

Bài 4 (trang 100 sgk Đại Số và Giải Tích 11 nâng cao): Chứng minh rằng với mọi số nguyên n ≥ 2 ta luôn có đẳng thức sau:

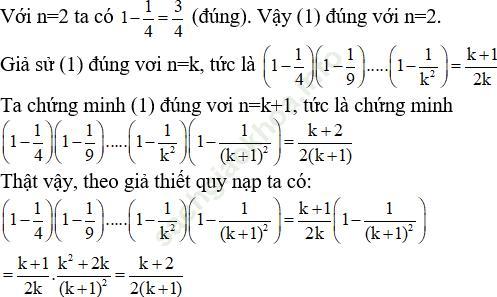
Vậy (1) đúng với n=k+1. Suy ra điều phải chứng minh.

Bài 5 (trang 100 sgk Đại Số và Giải Tích 11 nâng cao): Cho n là một số nguyên lớn hơn 1. Hãy chứng minh bất đẳng thức sau:

Bài 6 (trang 100 sgk Đại Số và Giải Tích 11 nâng cao): Với mọi số nguyên dương n, đặt u_n = 7.2^{2n - 2} + 3^{2n - 1}(1). Chứng minh rằng với mọi số nguyên dương n ta có u_n chia hết cho 5.

Với n = 1 ta có: u₁ = 7.2^{2.1 - 2} + 3^{2.1 - 1} = 10 chia hết cho 5.

Vậy (1) đúng với n = 1.

Giả sử (1) đúng với n=k, ta chứng minh nó cũng đúng với n = k + 1.

Thật vậy ta có:

u_{k + 1} = 7.2^{2 (k + 1) - 2} + 3^{2 (k + 1) - 1} = 4.7.2^{2k - 2} + 9.3^{2k - 1}

= 4. (7.2^{2k - 2} + 3^{2k - 1}) + 5.3^{2k - 1} = 4. u_k + 5.3^{2k - 1} (2)

Vì u_k chia hết cho 5 theo giả thiết quy nạp nên từ (2) suy ra điều phải chứng minh.

Bài 7 (trang 100 sgk Đại Số và Giải Tích 11 nâng cao): Cho số thực x > -1. Chứng minh rằng (1 + x)ⁿ ≥ 1 + nx (1) với mọi n nguyên dương.

Với n=1 ta có (1 + x)¹ = 1 + x = 1 + 1. x. Vậy (1) đúng vơi n = 1.

Giả sử (1) đúng vơi n=k, ta chứng minh nó đúng với n = k + 1.

Thật vậy, từ giải thiết quy nạp và x > -1 ta có:

(1 + x)^{k + 1} = (1 + x). (1 + x)^k ≥ (1 + x)(1 + kx) = 1 + (k + 1)x + kx² ≥ 1 + (k + 1)x

Từ đó suy ra điều phải chứng minh.

Bài 8 (trang 100 sgk Đại Số và Giải Tích 11 nâng cao): Một học sinh chứng minh mệnh đề “với k là số nguyên dương tùy ý, nếu 8^k + 1 chia hết cho 7 thì 8^{k + 1} + 1 cũng chia hết cho 7” như sau: Ta có: 8^{k + 1} + 1 = 8 (8^k + 1) - 7. Từ đây và giả thiết 8^k + 1 chia hết cho 7 suy ra 8^{k + 1} + 1 cũng chia hết cho 7.

Hỏi cách chứng minh trên, bạn học sinh đó có thể kết luận được 8ⁿ + 1 chia hết cho 7 với mọi n nguyên dương không? Vì sao?

Không thể kết luận được 8ⁿ + 1 chia hết cho 7 với mọi n nguyên dương vì chưa kiểm tra tính đúng của mệnh đề đó khi n = 1.