Bài 5: Khoảng cách - Giải BT Toán 11 nâng cao
Chương III. Vectơ trong không gian. Quan hệ vuông góc
Bài 5: Khoảng cách
Bài 29 (trang 117 sgk Hình học 11 nâng cao): Cho tứ diện ABCD có:
AC = BC = AD = BD = a, AB = c, CD = c’.
Tính khoảng các giữa hai đường thẳng AB và CD.
Bài giải: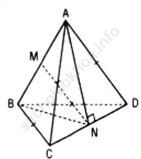
Gọi M, N lần lượt là trung điểm của AB và CD.
Δ ACD cân nên AN ⊥ CD
Δ BCD cân nên BN ⊥ CD
Do đó CD ⊥ (ABN) ⇒ CD ⊥ MN. Tương tự AB ⊥ MN.
Vậy d (AB, CD) = MN

Bài 30 (trang 117 sgk Hình học 11 nâng cao): Cho hình lăng trụ ABC. A’B’C’ có tất cả các canh đều bằng a. Góc tạo bởi cạnh bên và mặt phẳng đáy bằng 30˚. Hình chiếu H của điểm A trên mặt phẳng (A’B’C’) thuộc đường thẳng B’C’.
a) Tính khoảng cách giữa hai mặt phẳng đáy.
b) Chứng minh rằng hai đường thẳng AA’ và B’C’ vuông góc, tính khoảng cách giữa chúng.
Bài giải: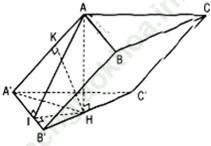

Bài 31 (trang 117 sgk Hình học 11 nâng cao): Cho hình lập phương ABCD A’B’C’D’có cạnh bằng a. Tính khoảng cách giữa hai đường thẳng BC’ và CD’
Bài giải: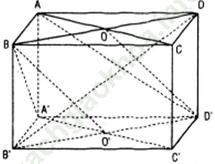
Gọị O, O’ lần lượt là tâm các hình vuông ABCD, A’B’C’D’ của hình lập phương ABCD. A’B’C’D’ cạnh a

Từ (1) và (2) suy ra B’D ⊥ (BA'C').
Tương tự chứng minh được B’D ⊥ (ACD')
+ Hai mặt phẳng (BA’C’) và (ACD’) song song với nhau, vuông góc với đoạn B’D và chia B’D thành 3 phần bằng nhau (xét hình bình hành BB’DD’ và BO // D’O).
Do đó khoảng cách giữa mp (BA’C’) và mp (ACD’) là B'D/3= (a√3)/3
+ Khoảng cách giữa BC’ và CD’
Khoảng cách giữa hai đường chéo nhau BC’ và CD’ bằng khoảng cách giữa hai mặt phẳng song song: mp (BA’C’) và mp (ACD’). Vậy khoảng cách đó là (a√3)/3
Bài 32 (trang 117 sgk Hình học 11 nâng cao): Cho hình hộp chữ nhật ABCD. A’B’C’D’ có AB = AA’ = a, AC’ = 2a
a) Tính khoảng cách từ điểm D đến mặt phẳng (ACD’).
b) Tính đường vuông góc chung của các đường thẳng AC’ và CD’. Tính khoảng các giữa hai đường thẳng ấy.
Bài giải: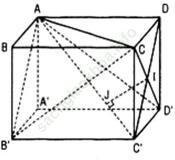
a) Xét tứ diện DACD’ có DA, DC, DD’ đôi một vuông góc nên khoảng cách DH từ D đến mp (ACD’) được tính bởi hệ thức:

b) Vì CD = DD’ = a nên CD’ ⊥ C’D. Mặt khác AD ⊥ (CDD’C) nên CD’ ⊥ AC’ và CD’ ⊥ mp (AC’D). Gọi giao điểm của CD’ với mp (AC’D) là I. Trong mặt phẳng (AC’D) Kẻ IJ vuông góc với AC’ tại J thì IJ là đường vuông góc chung của AC’ và CD’.
Ta tính khoảng cách giữa AC’ và CD’.

Bài 33 (trang 118 sgk Hình học 11 nâng cao):
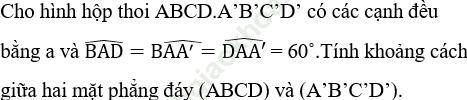
Bài giải:
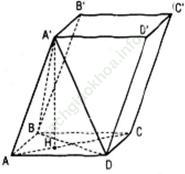
Từ giả thiết suy ra các tam giác A’AD, BAD, A’AB là các tam giác cân cùng có góc ở đỉnh bằng 60 ˚ nên chúng là các tam giác đều. Như vậy tứ diện A’ABD có các cạnh cùng bằng a hay A’ABD là tứ diện đều. Khi đó hình chiếu của A’ trên mặt phẳng (ABCD) chính là trọng tâm H của tam giác đều ABD. Khoảng cách giữa hai mặt phẳng đáy (ABCD) và (A’B’C’D’) chính là độ dài A’H. Ta có
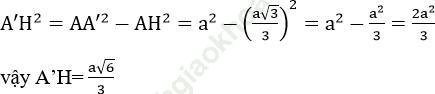
Bài 34 (trang 118 sgk Hình học 11 nâng cao): Cho hình chóp S. ABCD có đáy là hình chữ nhật và AB = 2a, BC = a. Các cạnh bên của hình chóp bằng nhau và bằng a√2
a) Tính khoảng cách từ S đến mặt phẳng đáy (ABCD)
b) Gọi E và F lần lượt là trung điểm của các canh AB và CD; K là điểm bất kì thuộc đường thẳng AD. Chứng minh rằng khoảng cách giữa hai đường thẳng EF và SK không phụ thuộc vào k, hãy tính khoảng cách đó theo a.
Bài giải: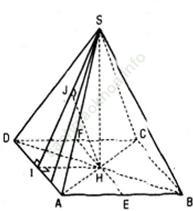
a) Vì SA = SB = SC = SD = a√2 nên hình chiếu của điểm S trên mặt phẳng (ABCD) là điểm H mà HA = HB = HC = HD. Do ABCD là hình chữ nhật nên H chính là giao điểm của AC và BD. Khoảng cách từ S đến mp (ABCD) bằng SH. Ta có:
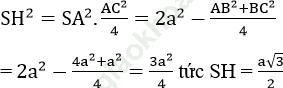
b) Vì EF // AD nên EF // mp (SAD), mặt khác SK nằm trong mp (SAL) nên khoảng cách giữa EF và SK chính là khoảng cách giữa EF và mp (SAD), đó cũng chính là khoảng cách từ H đến mp (SAD). Vậy khoảng cách giữa EF và SK không phụ thuộc vào vị trí của điểm K trên đường thẳng AD.
Tính d (EP; SK):
Gọi I là trung điểm của AD, kẻ đường cao HJ của tam giác vuông SHI thì HJ ⊥ mp (SAD) do đó d (H; (SAD)) = HJ. Ta có: HJ. SI = SH. HI

Như vậy khoảng cách giữa EF và SK không phụ thuộc vào vị trí của điểm K trên đường thẳng AD và bằng (a√21)/7.
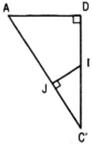
Bài 35 (trang 118 sgk Hình học 11 nâng cao): Cho tứ diện ABCD. Chứng minh rằng nếu AC = BD, AD = BC thì đường vuông góc chung của AB và CD là đường thẳng nối trung điểm của AB và CD. Điều ngược lại có đúng k?
Bài giải: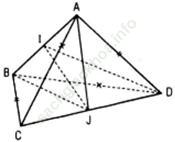
a) Vì AC = BD, AD = BC nên tam giác ACD bằng tam giác BDC, từ đó hai trung tuyến tương ứng AJ và BJ bằng nhau (ở đó J là trung điểm của CD). Gọi I là trung điểm của AB thì ta có JI ⊥ AB. Tương tự như trên ta cũng có JI ⊥ CD. Vậy IJ là đường vuông góc chung của AB và CD.
b) Điều ngược lại của kết luận nêu ra trong bài toán cũng đúng, tức là nếu CJ ⊥ AB, IJ ⊥ CD, I, J lần lượt là trung điểm của AB và CD thì AC = BD; AD = BC
Thật vậy vì IJ ⊥ AB, I là trung điểm của AB nên AJ = BJ. Mặt khác:
