Bài 2: Phương trình lượng giác cơ bản - Giải BT Toán 11 nâng cao
Chương 1: Hàm số lượng giác và phương trình lượng giác
Bài 2: Phương trình lượng giác cơ bản
Bài 14 (trang 28 sgk Đại Số và Giải Tích 11 nâng cao): Giải các phương trình sau:
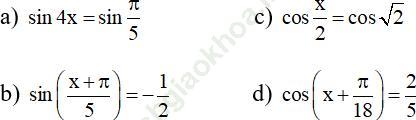
Bài giải:


Bài 15 (trang 28 sgk Đại Số và Giải Tích 11 nâng cao):
a) Vẽ đồ thị của hàm số y = sinx rồi chỉ ra trên đồ thị đó những điểm có hoành độ thuộc khoảng (-π, 4π) là nghiệm của mỗi phương trình sau:
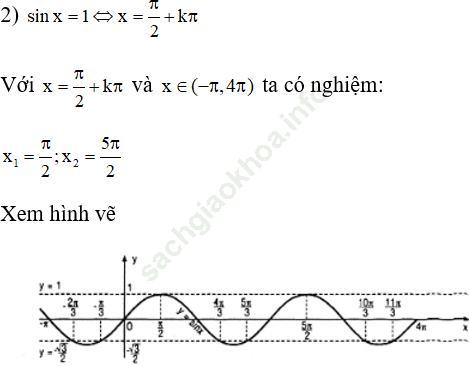
1) sinx = -√ 3/2
2) sinx = 1
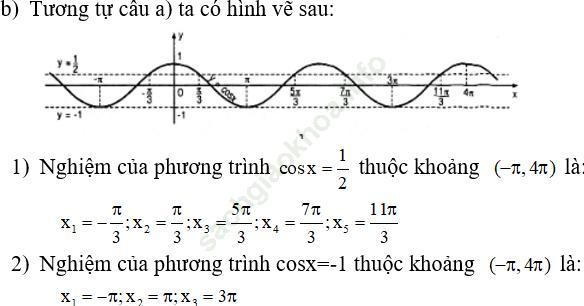
b) Cũng câu hỏi tương tự cho hàm số y = cosx đối với mỗi phương trình sau:
1) cosx = 1/2
2) cosx = -1
Bài giải: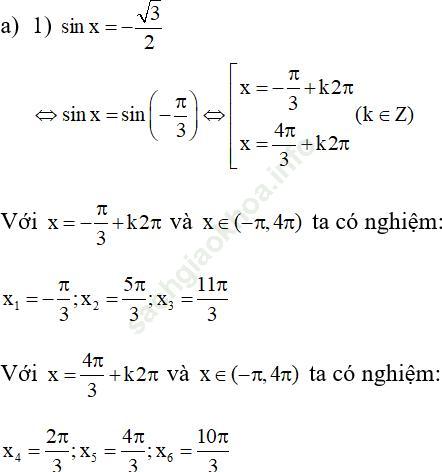
Bài 16 (trang 28 sgk Đại Số và Giải Tích 11 nâng cao): Tìm nghiệm của các phương trình sau trong khoảng đã cho:
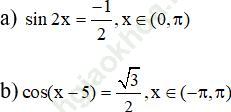


Bài 17 (trang 29 sgk Đại Số và Giải Tích 11 nâng cao): Số giờ có ánh sang mặt trời ở thành phố A ở vĩ độ 40o bắc trong ngày thứ t của một năm không nhuận được cho bởi hàm số:
a) Thành phố A có đúng 12 giờ có ánh sang mặt trời vào ngày nào trong năm?
b) Vào ngày nào trong năm thì thành phố A có ít giờ có ánh sáng mặt trời nhất?
c) Vào ngày nào trong nằm thì thành phố A có nhiều giờ có ánh sáng mặt trời nhất?
Bài giải:a)

Vậy thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày thứ 30 (ứng với k = 0) và ngày thứ 262 (ứng với k = 1) trong năm.
b)

Vậy nên thành phố A có ít giờ có ánh sáng mặt trời nhất (9 giờ) vào ngày thứ 353 trong năm.
c)

Vậy nên thành phố A có nhiều giờ có ánh sáng mặt trời nhất (15 giờ) vào ngày thứ 171 trong năm.
Bài 18 (trang 29 sgk Đại Số và Giải Tích 11 nâng cao): Giải các phương trình sau:
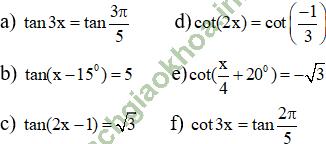

Bài 19 (trang 29 sgk Đại Số và Giải Tích 11 nâng cao):
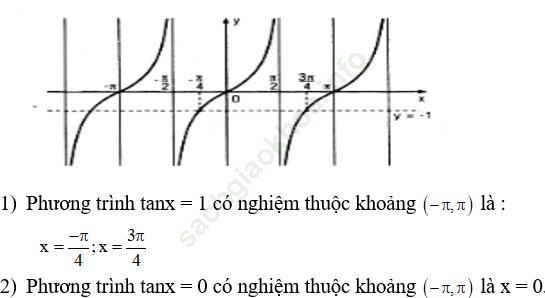
a) Vẽ đồ thị hàm số y = tanx rồi chỉ ra trên đồ thị đó những điểm có hoành độ thuộc khoảng (-π; π) là nghiệm của mỗi phương trình sau:
1) tanx = -1
2) tanx = 0
b) Cũng câu hỏi tương tự cho hàm số y = cotx cho mỗi hàm số sau:
1) cotx = √ 3/3
2) cotx = 1
Bài giải:a)
b)
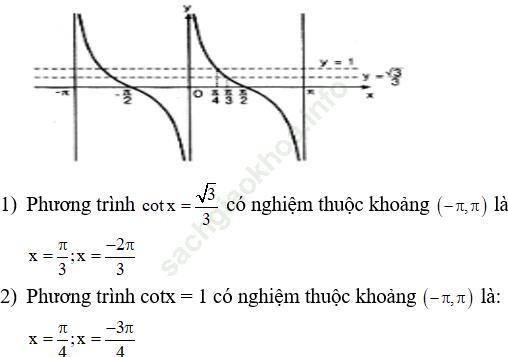
Bài 20 (trang 29 sgk Đại Số và Giải Tích 11 nâng cao): Tìm nghiệm của các phương trình sau trên khoảng đã cho:
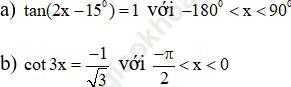
a)
tan (2x - 15o) = 1 ⇔ 2x = 15o + 45o + k180o ⇔ x = 30o + k90o
- 180o < 30o + k90o ⇔ -2 < 1/3 + k < 1 ⇔ k ∈ {-2,1,0}
Vậy các nghiệm của phương trình là x = -150o, x = -60o, x = 30o
b)

Bài 21 (trang 29 sgk Đại Số và Giải Tích 11 nâng cao):

Theo em, ai giải đúng, ai giải sai?
Bài giải:Theo em, cả hai bạn đều giải ĐÚNG. Hai họ nghiệm chỉ khác nhau về hình thức, thực chất chỉ là một.
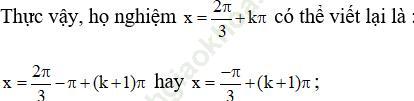
đây chính là kết quả mà Phương tìm được.
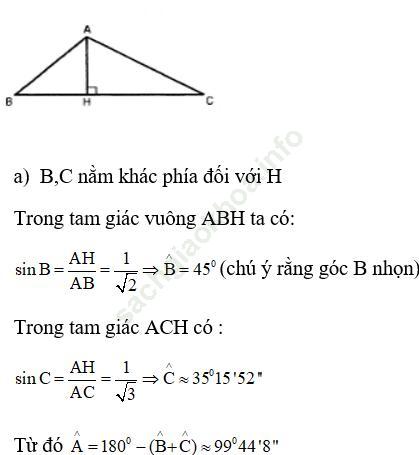
Bài 22 (trang 30 sgk Đại Số và Giải Tích 11 nâng cao): Tính các góc của tam giác ABC biết AB = √ 2 cm; AC = √ 3 cm và đường cao AH = 1cm. (Gợi ý: Xét trường hợp B, C nằm khác phía đối với H và trường hợp B, C nằm cũng phía đối với H).
Bài giải:Ta xét hai trường hợp: