Luyện tập (trang 8-9) - Giải BT Toán 12 nâng cao
Bài 6 (trang 8 sgk Giải Tích 12 nâng cao): Xét chiều biến thiên của hàm số sau:
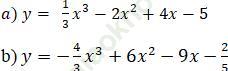
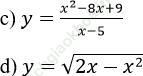
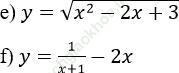
Bài giải:
a. Hàm số đã cho xác định trên R.
Ta có đạo hàm: y'=x2-4x+4= (x-2)2≥0, ∀x
y'=0 chỉ tại x = 2
=> Hàm số đồng biến trên R.
b. Hàm số đã cho xác định trên R.
y'= -4x2+12x-9 = - (2x-3)2≤ 0, ∀x ∈R; y'=0 chỉ tại x = 3/2
=> Hàm số nghịch biến trên R.
c. Hàm số đã cho xác định trên D = R \ {5}
Ta có đạo hàm:
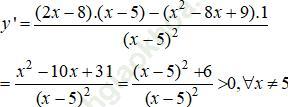
Nên hàm số đồng biến trên khoảng (-∞; 5) và (5; +∞)
Tập xác định: D= [0; 2]
Hàm số đã cho liên tục trên đoạn [0; 2]
Đạo hàm
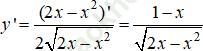
y’=0 ⇔ x=1
Bảng biến thiên:
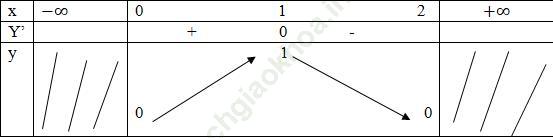
Vậy hàm số đồng biến trên [0; 1] và nghịch biến trên [1; 2]. Hoặc có thể nói hàm số đồng biến trên (0; 1) nghịch biến trên (1; 2).
Vì (x2-2x+3 = (x-1)2+2 > 0 ∀x ∈R)
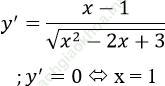
Bảng biến thiên
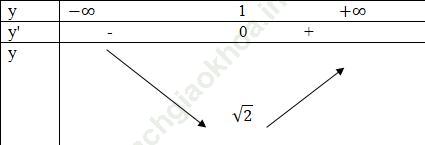
Hàm số nghịch biến trên (-∞; 1), đồng biến trên (1; +∞)
f. Hàm số xác định trên D = R \ {-1}
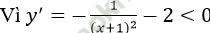
∀x ∈D nên hàm số nghịch biến trên mỗi khoảng (-∞; -1)và (-1; +∞)
Bài 7 (trang 8 sgk Giải Tích 12 nâng cao): CMR: hàm số f (x) = cos2x - 2x + 3 nghịch biến trên R.
Bài giải:f (x) xác định và liên tục trên R nên liên tục trên mỗi đoạn
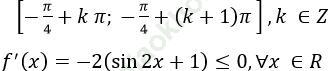
f’ (x) = 0 < => sin 2x = -1 < => 2x = -π /2+k2 π < => x=-π /4+k π, k ∈Z
Vậy hàm số nghịch biến trên mỗi đoạn
=> Hàm số nghịch biến trên R.
Bài 8 (trang 8 sgk Giải Tích 12 nâng cao): Cmr bất đẳng thức sau:
+) sin x< x với mọi x > 0;
+) sin x > x với mọi x < 0.
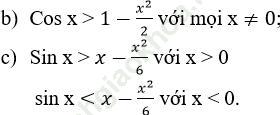
Bài giải:
a.
+) Xét hàm số f (x) = x - sinx hàm số này liên tục trên R.
+ Xét hàm số trên nửa khoảng ![]()
Đạo hàm f’ (x) = 1 - cosx > 0 ![]()
=> Hàm số đồng biến trên ![]()
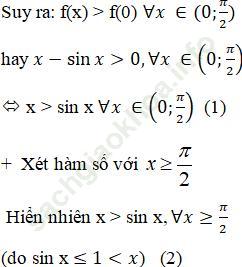
Từ (1) và (2) suy ra, x > sin x với x > 0.
+) Xét hàm số y= x - sin x liên tục trên R.
+ Hàm số f (x) = x – sin x trên ![]() có đạo hàm f’ (x) = 1 - cos x > 0
có đạo hàm f’ (x) = 1 - cos x > 0 ![]()
=> Hàm số đồng biến trên ![]()
⇒ f (x) < f (0) hay x- sin x
+ Hiển nhiên: x < sin x với mọi ![]()
Từ (3) và (4) suy ra; x < sin x với mọi x < 0
b. Hàm số ![]() xác định trên R và có đạo hàm g’ (x) = x – sin x
xác định trên R và có đạo hàm g’ (x) = x – sin x
Dựa vào ý a) và chú ý x- sin x = 0 ⇔ x = 0, ta có bảng biến thiên của hàm g (x)
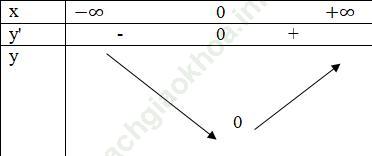
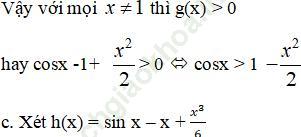
Tập xác định D = R và có đạo hàm ![]()
Suy ra, h (x) đồng biến trên R.
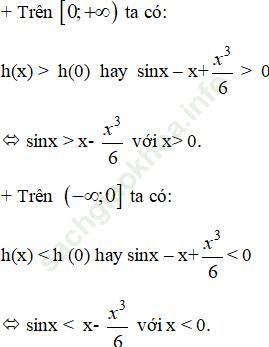
Bài 9 (trang 9 sgk Giải Tích 12 nâng cao): CMR: sinx + tanx > 2x với mọi x ∈ (0; π /2)
Bài giải: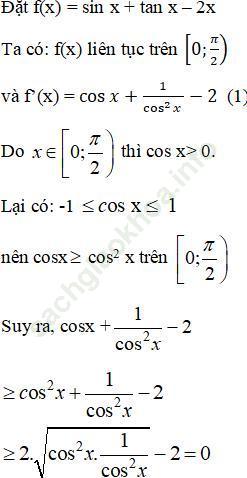
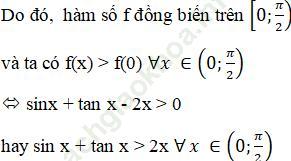
Bài 10 (trang 9 sgk Giải Tích 12 nâng cao):
Số dân của một thị trấn t năm kể từ năm 1970 ước tính bởi công thức
a. Tính số dân của thị trấn vào đầu năm 1908 và đầu năm 1995
b. Xem f là một hàm số xác định trên nửa khoảng [0; +∞). Tính f’ (t) và xét chiều biến thiến của h trên nửa khoảng [0; +∞)
c. Đạo hàm của hàm số f biểu thị tốc độ tăng dần của thị trấn (tính bằng nghìn người/năm)
+ Tính tốc độ tăng dân số vào năm 1990 của thị trấn.
+ Tính tốc độ tăng dân số được dự kiến vào năm đầu 2008.
+ Vào năm nào thì tốc độ tăng dần số là 0,125 nghìn /người.
Bài giải:a. Vào đầu năm 1980, ta có t = 10; f (10)= ![]()
Vậy số dân của thị trấn vào đầu năm 1980 là 18 nghìn người.
Vào đầu năm 1995, ta có t = 25, f (25) = 22
=> Số dân của thị trấn vào đầu năm 1995 là 22 nghìn người.
f (t) liên tục trên [0; +∞) (vì liên tục trên khoảng (-5; +∞))
=> Hàm số đồng biến trên [0; +∞)
c.
+ Tốc độ tăng dân số vào đầu năm 1990 là:
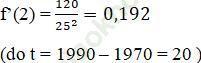
+ Tốc độ tăng dân số được dự kiến vào năm 2008 của thị trấn là:
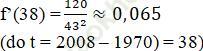
+ Ta có f’ (t) = 0,125
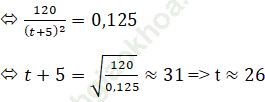
Vậy năm 1996, tốc độ tăng dân số của thị trấn là 0,125 nghìn người / năm