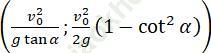Bài 8: Một số bài toán thường gặp về đồ thị - Giải BT Toán 12 nâng cao

Bài 57 (trang 55 sgk Giải Tích 12 nâng cao):

a) Khảo sát sự biến thiên và đồ thị (C) hàm số: f (x)=2x³+3x²+1

b) Tìm các giao điểm của đường cong (C) và parapol g (x) = 2x²+1 (P)

c) Viết Phương trình các tiếp điểm của (C) và (P) tại các điểm của chúng.

d) Xác định các khoảng trên đó (C) nằm phía trên và hoặc phía dưới (P).

Bài giải:

a) Hàm số: f (x) = y=2x³+3x²+1.

TXĐ: D = R

Đạo hàm: y’ = 6x²+6x

Sự biến thiên

Hàm số đồng biến trong khoảng (-∞; -1) và (0; +∞)

Hàm số nghịch biến trong khoảng (-1; 0)

Cực trị: y_CĐ = 2 khi x = -1

y_CT = 1 khi x = 0

Điểm uốn, tính lồi lõm:

Ta có y’’ = 12x + 6

y'' = 0 < => 12x+6 = 0 < => x = -1/2 => y = 3/2

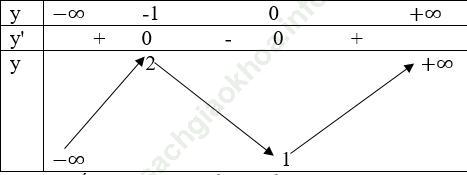
Bảng xét dấu

Bảng biến thiên

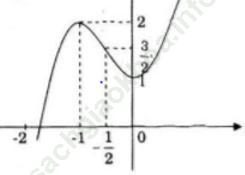
Đồ thị hàm số: f (x) = y = 2x³+3x²+1

Giao điểm Oy: (0; 1)

Đi qua (-1; 2)

b) Hoành độ giao điểm của đường cong (C) và parabol (P) là nghiệm của phương trình:

f (x) = g (x) < => 2x³+3x²+1 = 2x²+1

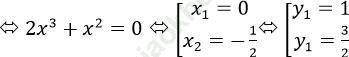
Vậy đường cong C và parabol (P) cắt tại 2 điểm: A (0; 1); B (-1/2; 3/2)

c) Hệ số góc tiếp tuyến tại điểm A của đường cong (C) và parabol (P) là: y’ (0) = 0

=> Phương trình tiếp tuyến tại giao điểm A của đường cong (C) và parabol (P) y = 0 (x- 0)+ 1 hay y = 1

Hệ số số góc tiếp tuyến tại giao điểm B của đường cong (C) và parabol (P) là:

Vậy Phương trình tiếp tuyến tại giao điểm B của đường cong (C) và parabol (P) là:

d) Để (C) nằm phía trên (P) thì 2 hàm số f (x) và g (x) phải thõa mãn điều kiện sau:

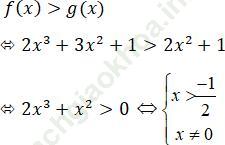
Vậy với x > -1/2 và x ≠ 0 thì (C) nằm phía trên (P).

Để (C) nằm phía dưới (P) thì 2 hàm số f (x) và g (x) thỏa mãn điều kiện sau:

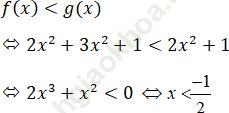
Vậy với x < -1/2 thì (C) nằm phía dưới (P).

Bài 58 (trang 56 sgk Giải Tích 12 nâng cao):

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số

b) Với các giá trị nào của m thì (d_m) đi qua điểm A (-2; 2) và có hệ số góc m cắt đồ thị của hàm số đã cho.

- Tại 2 điểm phận biệt?

- Tại 2 điểm thuộc 2 nhánh 2 của đồ thị?

Bài giải: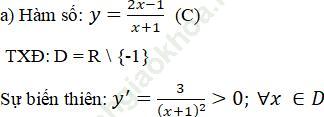

- Hàm số luôn đồng đồng biến trong khoảng (-∞; -1)và (-1; +∞)

- Hàm số không có cực trị.

Vậy đồ thị hàm số có tiệm cận đứng là đường thẳng: x = -1.

Vậy đồ thị hàm số có tiệm cận ngang là đường thẳng: y = 2.

Bảng biến thiên

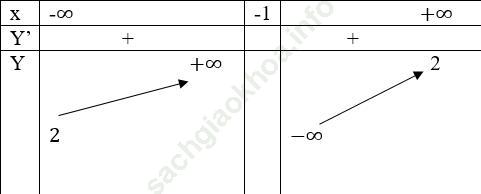
Đồ thị hàm số nhận điểm I (-1; 2) là giao điểm của 2 tiệm cận làm tâm đối xứng. Đồ thị đi qua A (0; -1), B (1/2; 0), C (1; 1/2);D (2; 1)

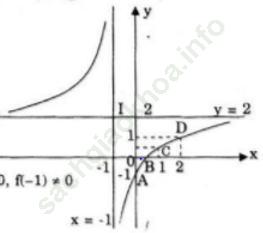
b) Đường thẳng (d_m) qua điểm A (-2; 2) có hệ số góc m là:

y=m (x+2)+2

⇔ y=mx+2m+2

Để (d_m) cắt đồ thị (C) tại 2 điểm phân biệt thì phương trình sau phải có 2 nghiệm phân biệt ≠ -1

⇔ f (x) = mx² + 3mx + 2m + 3 = 0 và f (-1) ≠ 0 (1)

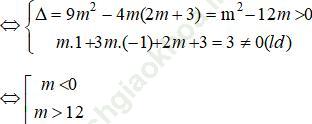
Vậy với m ∈ (-∞; 0) và (12, +∞) thì đường thẳng (d_m) sẽ cắt đồ thị hàm số (C) tại 2 điểm phân biệt.

- Để (d_m) cắt đồ thị hàm số (C) tại 2 điểm thuộc 2 nhánh của đồ thị thì:

x₁< -1< x₂ hay af (-1)< 0

⇔ m (m (-1)²+3m (-1)+2m+3)< 0 ⇔ 3m< 0 ⇔ m < 0

Vậy với m ∈ (-∞; 0) thì đường thẳng (d_m) sẽ cắt đồ thị (C) tại 2 điểm phân biệt ∈ 2 nhánh đồ thị.

Bài 59 (trang 56 sgk Giải Tích 12 nâng cao): Chứng minh rằng các đồ thị của 3 hàm số: f (x) = -x²+3x+6; g (x)=x³-x²+4 và h (x) = x²+7x+8 tiếp xúc với nhau tại điểm A (-1; 2)

Bài giải:

Để đồ thị của 3 hàm số trên tiếp xúc với nhau tại A (-1; 2) thì 3 đồ thị đó có tiếp tuyến chung tại điểm A

⇔ hệ số góc của các tiếp tuyến tại điểm A bằng nhau. Ta có:

+ f’ (x) = -2x+3 ⇒ f' (-1)=5

+ g’ (x) = 3x²-2x ⇒ g' (-1)=5

+ h’ (x) = 2x+7 ⇒ h' (-1)=5

Vậy 3 hàm số trên tiếp xúc với nhau nhau tại A (-1; 2)

Bài 60 (trang 56 sgk Giải Tích 12 nâng cao): Chứng minh rằng các đồ thị của hai hàm số

tiếp xúc với nhau. Xác định tiếp tuyến của 2 đường cong trên và viết Phương trình tiếp tuyến chung của chúng tại điểm đó.

Bài giải:

Hai hàm số f (x) và g (x) tiếp xúc với nhau khi và chỉ khi hệ phương trình sau có nghiệm:

Vậy 2 đường cong trên cắt nhau tại M (0; 0)

Phương trình tiếp tuyến chung của f (x) và g (x) có hệ số góc k là: k = f’ (0) = 3/2

Vậy Phương trình tiếp tuyến chung của f (x) và g (x) là: y=3x/2

Bài 61 (trang 56 sgk Giải Tích 12 nâng cao): Một viên đạn được bắn ra với vận tốc ban đầu v₀ > 0 từ một nòng súng đặt ở gốc tọa độ O, nghiêng một góc α với mặt đất (nòng súng nằm trong mặt phẳng đứng thẳng Oxy và tạo với trục hoành Ox một góc α. Biết quỹ đạo chuyển động của viên đạn là parabol.

g là gia tốc trọng trường.

chứng minh rằng với mọi α ∈ (0; π /2) γ α luôn tiếp xúc với parabol (C) có phương trình là

và tìm tọa độ điểm (C) được gọi là parabol an toàn.

Bài giải: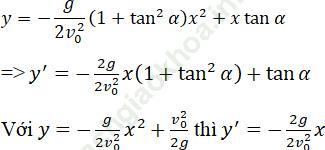

Tọa độ giao điểm M của (γ_α) và (C) là nghiệm của hệ phương trình sau:

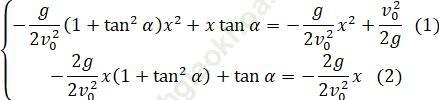
Giải (2)

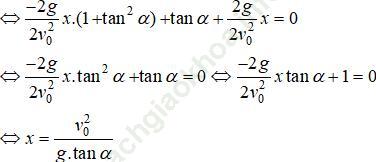
Thế vào (1) ta thấy thõa mãn.

⇒ Tiếp điểm M có tọa độ:

Bài trước: Luyện tập (trang 50) - Giải BT Toán 12 nâng cao Bài tiếp: Luyện tập (trang 57-58) - Giải BT Toán 12 nâng cao