Bài 1: Nguyên hàm - Giải BT Toán 12 nâng cao
Bài 1 (trang 141 sgk Giải Tích 12 nâng cao): Tìm nguyên hàm của các hàm số sau:
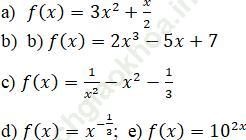
Bài giải:

Bài 2 (trang 141): Tìm:
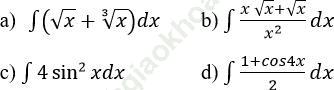
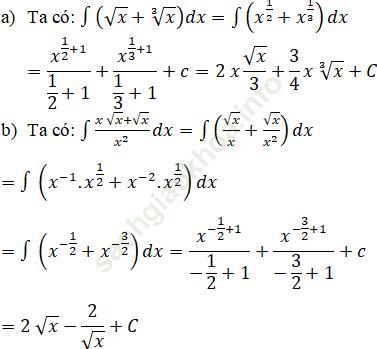
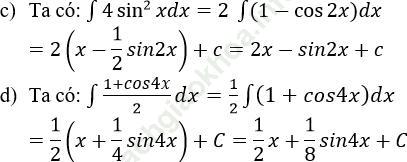
Bài 3 (trang 141): Chọn khẳng định đúng trong các khẳng định sau:
Nguyên hàm của hàm số y = x. sin x là:
A. x2 sin (x/2)+C
B. -xcos x +C
C. -x. cosx+sinx+C
Bài giải:Xét phương án C ta có:
(-x. cosx + sinx + C)’ = - (x. cosx)’ + (sinx)’ + C’ = - [1. cosx +x. (– sinx)] + cosx = x. sinx
Do đó nguyên hàm của hàm số y = x. sinx là F (x) = - x. cosx + sinx + C.
Đáp án đúng là: C.
Bài 4 (trang 141): Khẳng định sau đúng hay sai:
Nếu f (x) = (1-√ x)' thì ∫f (x) dx = -√ x + C
Bài giải:Khẳng định trên là đúng. Vì f (x) = (1-√ x)' = (-√ x)'