Câu hỏi và bài tập ôn tập chương 1 - Giải BT Toán 12 nâng cao
Bài 68 (trang 61 sgk Giải Tích 12 nâng cao): Chứng minh các bất đẳng thức sau:
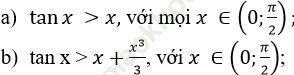
a) Xét hàm số f (x) = tan x – x
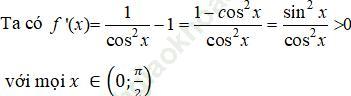
Do đó hàm số f (x) đồng biến trên (0; π/2)
Nên f (x) là hàm số đồng biến trên khoảng (0; π /2)
Vì f (0) = 0, nên khi x > 0 và x ∈ (0; π /2) thì f (x) > f (0), tức là tan x – x > 0 hay tan x > x.
b) Xét hàm số:
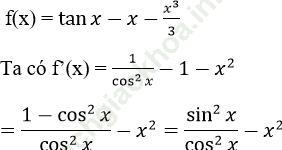
= tan2x-x2= (tanx-x) (tanx+x) > 0 với mọi x ∈ (0; π /2) và do câu a.
(Vì trên (0; π /2) thì tanx > 0 và x > 0 nên tanx + x > 0.
Lại theo câu a, trên khoảng (0; π /2) thì tanx – x > 0
Do đó, (tanx + x). (tanx – x) > 0).
=> f (x) là hàm số đồng biến trên khoảng (0; π /2)
Vì f (0) = 0 nên khi x > 0 thì f (x) > f (0), tức là tan x-x-x^3/3> 0 hay tanx > x+x3/3 với x ∈ (0; π /2)
Bài 69 (trang 61 sgk Giải Tích 12 nâng cao): Xét chiều biến thiên và tìm cực trị (nếu có) của hàm số sau:

Bài giải:
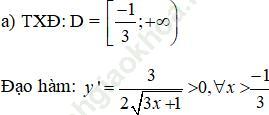
Suy ra hàm số đồng biến trên khoảng (-1/3; +∞). => hàm số chỉ có cực tiểu tại x=-1/3 và giá trị cực tiểu bẳng y (-1/3)=0.
b) Tập xác định D = [0; 4],
=> Hàm số đồng biến trên khoảng (0; 2), nghịch biến trên khoảng (2; 4). Hàm số đạt cực đại tại x = 2 và yCĐ = 2.
c) y=x+√ x. TXĐ: D = [0; +∞)
Đạo hàm ![]()
Vậy hàm số đồng biến trên khoảng (0; +∞)
=> hàm số đã cho không có điểm cực trị.
d) y = x-√ x, TXĐ: D = [0; +∞)
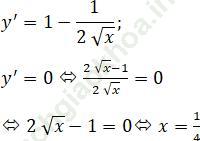
Hàm số đồng biến trên khoảng (1/4; +∞), nghịch biến trên khoảng (0; 1/4).
Vậy hàm số đạt cực tiểu tại x = 1/4 và giá trị cực tiểu y (1/4) = -1/4
Bài 70 (trang 61 sgk Giải Tích 12 nâng cao): Người ta định làm một cái hộp kim loại hình trụ có thể tích V cho trước. tìm bán kính đáy r và chiều cao h của hình trụ sao cho ít tốn kim loại nhất
Bài giải: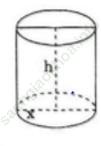

Để làm một cái hộp kim loại hình trụ ít tốn kim loại nhất thì diện tích toàn phần của hình trụ bé nhất.
Ta có

Bài 71 (trang 62 sgk Giải Tích 12 nâng cao): Chu vi một tam giác là 16 cm, độ dài một cạnh tam giác là 6 cm. Tìm độ dài hai cạnh còn lại của tam giác sao cho tam giác có diện tích lớn nhất.
Bài giải:Gọi độ dài ba cạnh của tam giác là 6, x và 10 – x, với 0 < x < 10
Nửa chu vi của tam giác là: p= 16: 2 = 8
Áp dụng công thức Hê-rông ta có diện tích tam giác là:
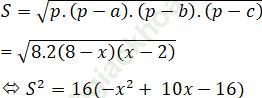
Để diện tích tam giác lớn nhất thì hàm số y=-x2+10x-16 đạt giá trị lớn nhất trên (0; 10).
Ta có y'=-2x+10; y'=0 ⇔ x = 5
Hàm số đồng biến trên (0; 5), nghịch biên trên khoảng (5; 10)
Vậy hàm số đạt giá trị lớn nhất tại x = 5.
Khi đó diện tích của tam giác lớn nhất bằng 12.
Vậy độ dài 2 cạnh còn lại đều là 5 cm.
Bài 72 (trang 62 sgk Giải Tích 12 nâng cao): Cho hàm số ![]()
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số đã cho.
b) CMR Phương trình f (x) = 0 có ba nghiệm phân biệt.
Bài giải:a) TXĐ: D = R
y' = x2-4x = x (x-4);
y'=0 ⇔ x = 0; x = 4
Hàm số đồng biến trên các khoảng (-∞, 0) và (4; +∞)
Hàm số nghịch biến trên khoảng (0; 4)
Hàm số đạt cực đại tại x = 0; yCĐ=y (0)=17/3
Hàm số đạt cực tiểu tại x = 4, yCT=y (4)=-5
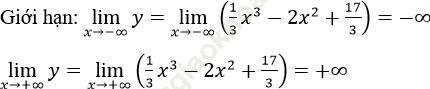
y''=2x-4; y''=0 ⇔ x = 2
Bảng xét dấu

Bảng biến thiên
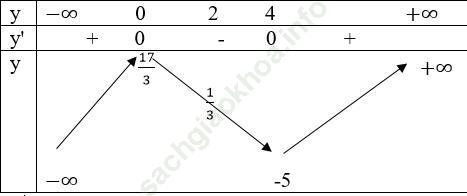
Đồ thị
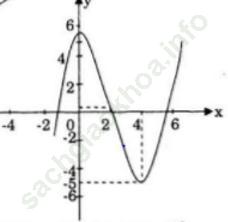
b) Đồ thị hàm số ![]() cắt trục hoành tại 3 điểm phân biệt. vậy phương trình f (x) = 0 có ba nghiệm phân biệt.
cắt trục hoành tại 3 điểm phân biệt. vậy phương trình f (x) = 0 có ba nghiệm phân biệt.
Bài 73 (trang 62 sgk Giải Tích 12 nâng cao): Cho hàm số f (x) = x3+px+q
a) Tìm điều kiện đối với p và q để hàm số f có cực đại và một cực tiểu.
b) CMR nếu có giá trị cực đại và giá trị cực tiểu trái dấu thì phương trình x3+px+q = 0 (1) có 3 nghiệm phân biệt.
c) CMR điều kiện cần và đủ để Phương trình (1) có ba nghiệm phân biệt là 4p3+27q2< 0
Bài giải:a) Đạo hàm: f' (x)=3x2+p
Để hàm số f (x) có một cực đại và một cực tiểu thì phương trình f’ (x) = 0 có 2 nghiệm phân biệt và f’ (x) đối dấu qua các điểm đó.
⇔ ∆’ = - 3p > 0 hay p < 0.
Vậy p < 0.
b) Cách 1
Dạng đồ thị như hình vẽ.
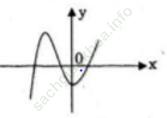
Đồ thị cắt trục hoành tại ba điểm phân biệt nên phương trình x3+px+q= 0 có 3 nghiệm phân biệt.
Cách 2
Hàm số f (x) = x3+px+q liên tục trên R và có
fCĐ=f (x1), fCT=f (x2)
Vì f (a).fCĐ < 0 nên phương trình có ít nhất 1 nghiệm thuộc (a, x1)
Và f (x1). f (x2) < 0 nên phương trình có ít nhất 1 nghiệm thuộc (x1,x2)
Vì f (x2), f (b)< 0 nên phương trình có ít nhất 1 nghiệm thuộc (x2,b)
Do Phương trình bậc ba có nhiều nhất là 3 nghiệm. vậy Phương trình x3+px+q=0 có 3 nghiệm phân biệt.
Lưu ý: khẳng định trên đúng với phương trình bậc ba tổng quát.
Gọi x1,x2 là hai điểm cực trị của hàm số.
Theo câu b, ta có điều kiện cần và đủ để phương trình (1) có ba nghiệm phân biệt là giá trị cực đại và cực tiểu trái dấu nhau,. Nghĩa là yCD.yCT< 0 < => f (x1). f (x2)< 0

Bài 74 (trang 62 sgk Giải Tích 12 nâng cao): Cho hàm số f (x) = x3-3x+1
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số.
b) Viết phương trình tiếp tuyến của đồ thị tại điểm uốn U của nó.
c) Gọi (dm) là đường thẳng đi qua U và có hệ số góc m. Tìm các giá trị của m sao cho đường thẳng (dm) cắt đồ thị của hàm số đã cho tại 3 điểm phân biệt.
Bài giải:a) TXĐ: D = R
y'=3x2-3; y'=0
< => 3x2-3=0
< => 3 (x2-1)=0
< => x = 1; x = -1
Hàm số đồng biến trên các khoảng (-∞, -1) và (1; +∞), nghịch biến trên khoảng (1-; 1)
yCĐ=y (-1)=3; yCT=y (1)=-1
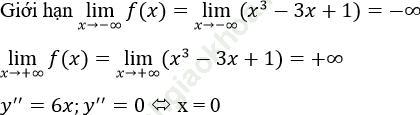
Bảng xét dấu

Bảng biến thiên
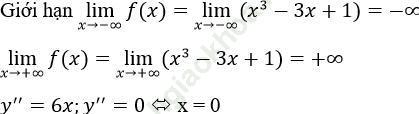
Đồ thị
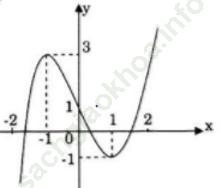
b) Phương trình tiếp tuyến của đồ thị tại điểm uốn U là: y-1=f' (0)(x-0)
⇔ y-1 = -3x hay y = -3x+1
c) Phương trình đường thẳng (m) đi qua điểm uốn U và có hệ số góc m có dạng y=mx+1
Hoành độ giao điểm của đường thẳng (dm) và đồ thị là nghiệm của phương trình:
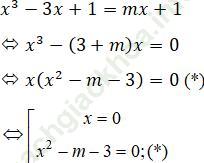
Để đường thẳng dm cắt đồ thị của hàm số đã cho tại ba điểm phân biệt thì phương trình (*) có 2 nghiệm phân biệt ≠ 0.
Vậy với m > -3 là giá trị cần tìm.
Bài 75 (trang 62 sgk Giải Tích 12 nâng cao): Cho hàm số y=x4- (m+1) x2+m
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số m = 2
b) Tìm các giá trị của m sao cho đồ thị hàm số cắt trục hoành tại bốn điểm, tạo thành 3 đoạn thẳng có độ dài bằng nhau.
Bài giải:a) Với m = 2. Hàm số có dạng: y=x4-3x2+2
TXĐ: D = R
y'=4x3-6x=2x (2x2-3);
y'=0
< => x = 0; x=√ 6/2; x= -√ 6/2
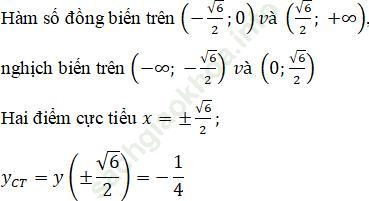
Điểm cực đại x = 0; yCD=y (0)=2
Giới hạn

Bảng biên thiên
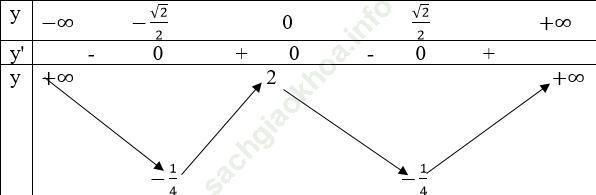
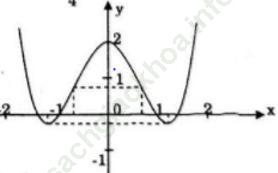
Đồ thị
Đồ thị cắt trục tung tại (0; 2)
Cắt trục hoành tại 4 điểm (-√ 2; 0); (-1; 0); (1; 0); (√ 2,0)
b) Đặt t = x2, điều kiện t ≥ 0. Hoành độ giao điểm của đồ thị và trục hoành là nghiệm của phương trình.
x4- (m+1) x2+m=0 (1)
< => t2- (m+1)t+m=0 (2)
Đồ thị của hàm số cắt trục tung tại 4 điểm tạo thành 3 đoạn thẳng có độ dài bằng nhau, tức là 4 điểm có hoành độ lập thành cấp số cộng.
< => Phương trình (2) có 2 nghiệm dương t1,t2 (với t1 < t2) thõa mãn điều kiện:
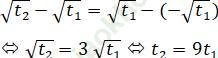
Điều kiện để (2) có 2 nghiệm dương phân biệt là:
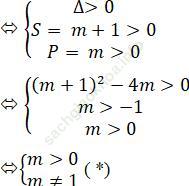
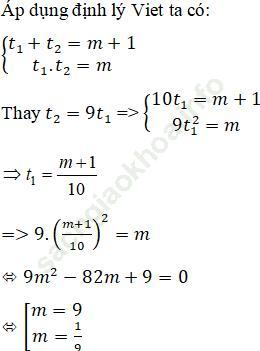
Kết hợp với điều kiện (*), => với m = 9 hoặc m = 1/9 thì đồ thị của hàm số cắt trục hoành tại 4 điểm, tạo thành 3 đoạn thẳng bằng nhau.
Bài 76 (trang 63 sgk Giải Tích 12 nâng cao): Cho hàm số f (x) = x4 - x2
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số đã cho.
b) Từ đồ thị hàm số f (x) suy ra đồ thị của hàm số y = |f (x)|
Bài giải:a) TXĐ: D = R
y' = 4x3-2x = 2x (2x2-1) = 0 < => x = 0; x=±√2/2
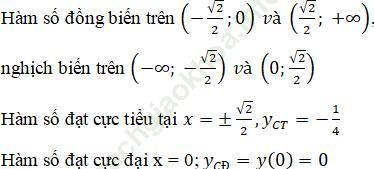
Điểm cực đại x = 0; yCĐ=y (0)=0
Giới hạn:
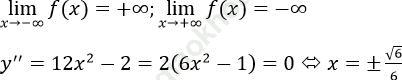

Bảng biến thiên
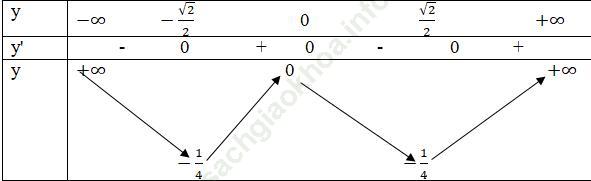
Đồ thị
Đi qua (0; 0); (-1; 0) và (1; 0)
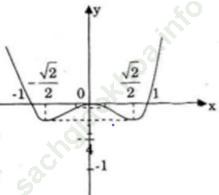
b) Gọi (C) là đồ thị của hàm số y= x4 – x2.
Và (C’) là đồ thị của hàm số y= | f (x) | = |x4 – x2 |
Ta thấy:
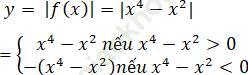
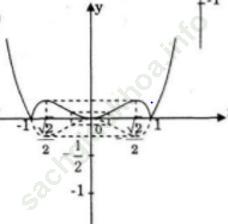
Cách vẽ đồ thị (C’):
+ Giữ nguyên phần đồ thị (C) bên trên trục Ox.
+ Lấy đối xứng phần đồ thị (C) bên dưới trục Ox qua trục Ox.
+ Hợp hai phần trên ta được đồ thị hàm số y = | f (x)|.
Bài 77 (trang 63 sgk Giải Tích 12 nâng cao): Cho hàm số ![]()
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số với m = 1
b) CMR với mọi m ≠ 1/2, các đường cong (Hm) đều đi qau hai điểm cố định A, B.
c) CMR tích các hệ số góc của tiếp tuyến với (Hm) tại hai điểm A và B là một hằng số khi m biến thiên.
Bài giải: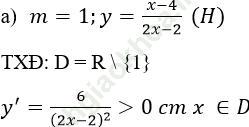
Nên hàm số đồng biến trên các khoảng (-∞; 1) và (1; +∞)
Do đó đường thẳng x = 1 là tiệm cận đứng.
=> đường thẳng y=1/2 là tiệm cận ngang.
Bảng biến thiên
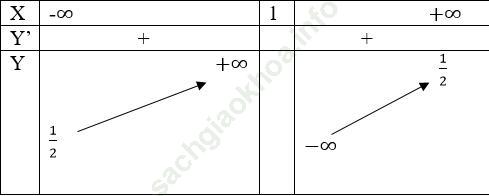
Đồ thị
Cặt trục tung tại (0; 2)
Cặt trục hoành tại (4; 0)
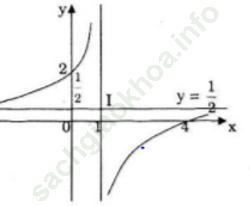
Điều kiện: mx ≠ 1
b) Gọi A (x, y) là điểm cố định của đồ thị hàm số khi m thay đổi.
Khi đó tọa độ của A thỏa mãn phương trình sau ∀m:
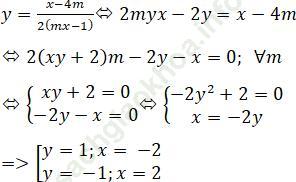
Vậy ∀m ≠ ±1/2 đồ thị hàm số luôn đi qua hai điểm cố định A (-2; 1), B (2; -1)
Hệ số của tiếp tuyến với (Hm) tại điểm A là y’ (2), tại điểm B là y’ (2)
Ta có:
Hệ số của tiếp tuyến với (Hm) tại điểm A là y’ (-2), tại điểm B là y’ (2)
Ta có:
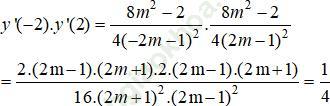
Vậy tích các hệ số góc của các tiếp tuyến với (Hm) tại 2 điểm A và B là 1 hằng số khi m biến thiên.
Bài 78 (trang 63 sgk Giải Tích 12 nâng cao):
a) Vẽ đồ thị (T) của hàm số y=x^2-x+1 và đồ thị (H) của hàm số ![]()
b) Tìm giao điểm của hai đường cong (T) và (H). CMR hai đường cong đó có tiếp tuyến chung tại giao điểm chung của chúng.
c) Xác định các khoảng trên đó (H) nằm phía trên hoặc dưới (H).
Bài giải:a) Đồ thị
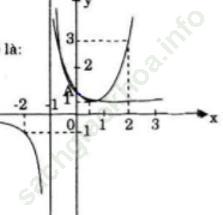
b)
Cách 1. Dựa vào đồ thị ta có giao điểm của (T) và (H) là A (0; 1)
Cách 2. Hoành độ giao điểm của (T) và (H) là nghiệm của phương trình.
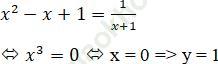
Vậy giao điểm của (T) và (H) là A (0; 1)
Phương trình tiếp tuyến của (T) tại A (0; 1) là:
y-1 = y' (0)(x-0)
⇔ y-1 = -x ⇔ y = -x+1
(với y’ (0) = 2.0 – 1 = -1)
Phương trình tiếp tuyến của (H) tại A (0; 1) là:
y-1 = y (0)(x-0) = -x ⇔ y = -x+1
Vậy hai đường cong đó có tiếp tuyến chung tại giao điểm của chúng.
c)
Cách 1. Dựa vào đồ thị ta thấy trên (-∞; -1) và (0; +∞), (P) nằm trên (H), trên (-1; 0) thì (P) nằm phía dưới (H).
Cách 2. Xét bất phương trình:
Trên (-1; 0), (P) nằm phía dưới (H).
Bài 79 (trang 63 sgk Giải Tích 12 nâng cao): Cho hàm số ![]()
a) Khảo sát và vẽ đồ thị (C) của hàm số.
b) Tiếp tuyến của đường cong (C) tại M (x0,y0) cắt tiệm cận đứng và tiệm cận xiên tại hai điểm A, B. CMR M là trung điểm trên đường cong (C).
Bài giải:a) TXĐ: D = R \ {0}
Hàm số đồng biến trên các khoảng (-∞; -1)và (1; +∞), nghịch biến trên (-1; 0) và (0; 1)
Hàm số đạt cực đại tại x = -1 và yCĐ=y (-1)=-2
Hàm số đạt cực tiểu tại x = 1 và yCT=y (1)=2
Giới hạn:
Vậy đường thẳng x = 0 là tiệm cận đứng.
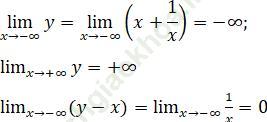
=> đường thẳng y = x là tiệm cận xiên.
Bảng biến thiên
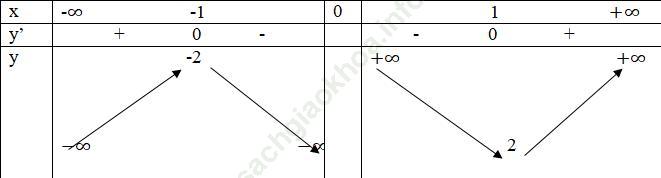
Đồ thị
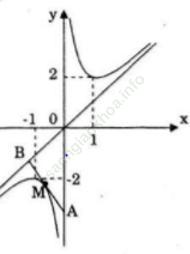
b) Phương trình tiếp tuyến tại điểm M (x0;y0) thuộc (C) là:
Δ cắt tiệm cận đứng tại A.
=> Tọa độ A (0; 2/x0)
Δ cắt tiệm cận xiên tại B.
=> Tọa độ B (2x0,2x0)
+ Tọa độ trung điểm của AB là:
Vậy M là trung điểm của đoạn AB.
+ Khoảng cách từ B đến trục Oy bằng 2x0 là độ dài đường cao kẻ từ B của OAB, OA có độ dài bằng 2/x0.
=> Diện tích tam giác OAB là (1/2).2x0. (2/x0) =2 không đổi (không phụ thuộc vào vị trị của M ∈ (C).