Ôn tập chương 5 - Giải BT Toán 11
Giải bài 1 trang 176 sgk Đại Số 11: Tìm các đạo hàm sau:
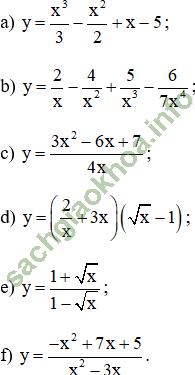
Bài giải:
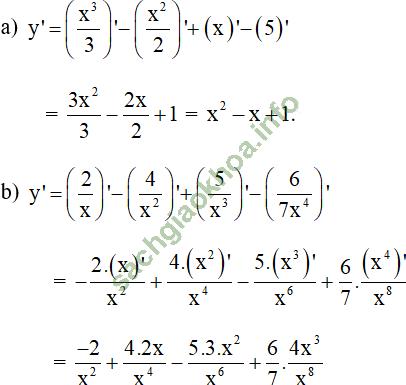
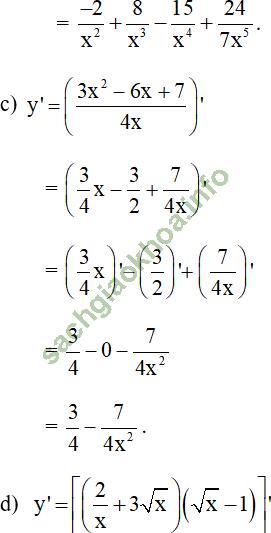
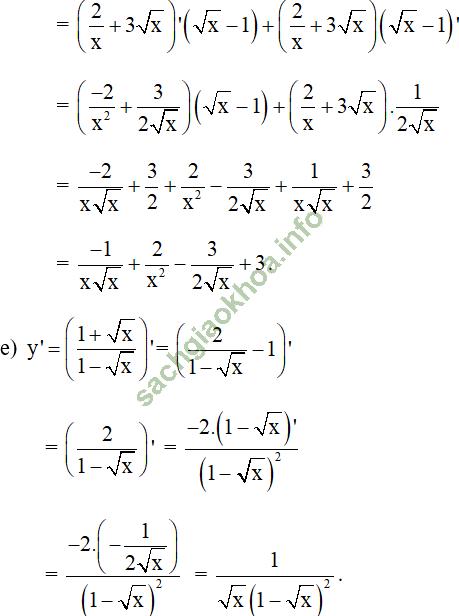

+ Với u = u (x); v = v (x) là các hàm số có đạo hàm tại x thuộc khoảng xác định ta có:
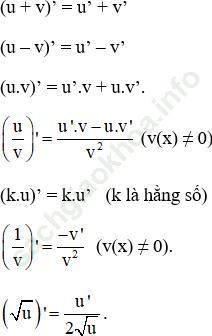
+ Đạo hàm của hàm hợp:
Hàm số y = f (u) với u = g (x) thì hàm số y = f (g (x)) có đạo hàm:
y’ = f’ (u).g’ (x).
Giải bài 2 trang 176 sgk Đại Số 11: Tìm đạo hàm của các hàm số sau:
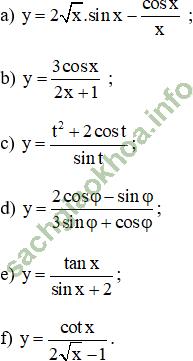
Bài giải:
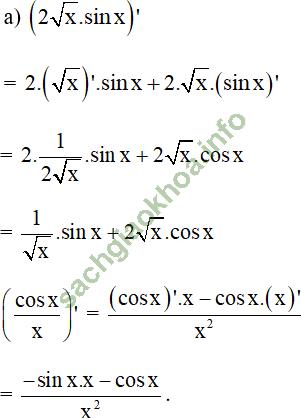

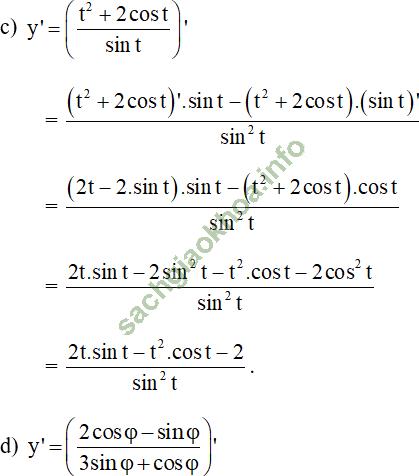
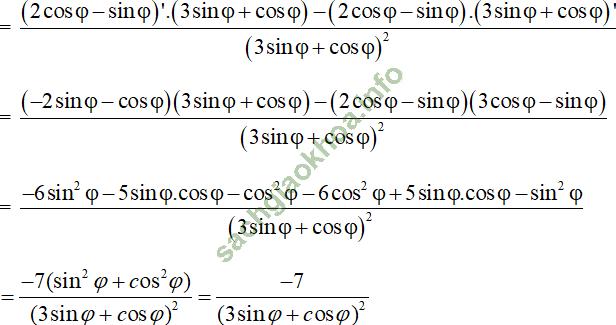
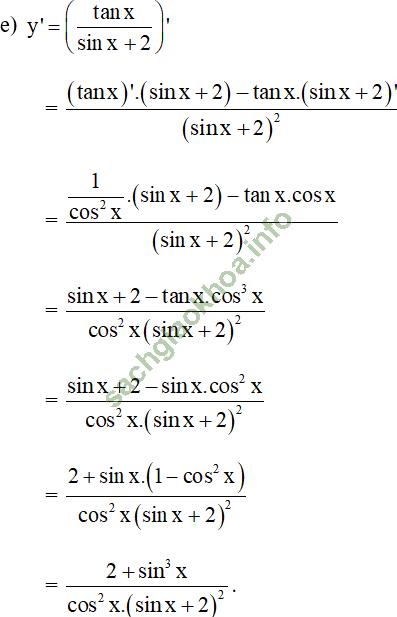
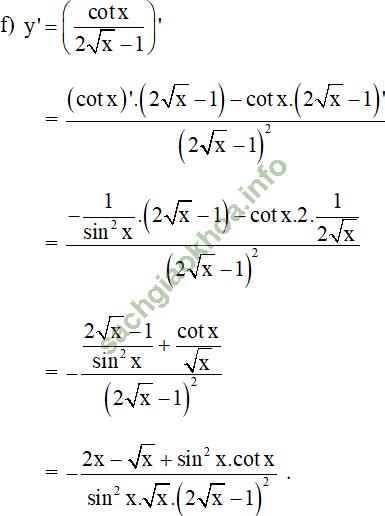

Giải bài 3 trang 176 sgk Đại Số 11: Cho hàm số 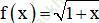
Tính f (3) + (x - 3)f’ (3)
Bài giải:
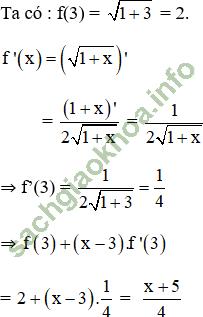
Giải bài 4 trang 176 sgk Đại Số 11: Cho hai hàm số f (x) = tan (x) và g (x) = 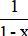 .
.
Tính 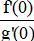
Bài giải:
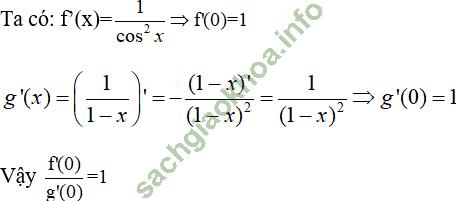
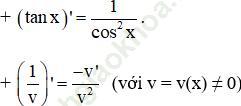
Giải bài 5 trang 176 sgk Đại Số 11: Giải phương trình f' (x) = 0, biết rằng:
![]()
Bài giải:
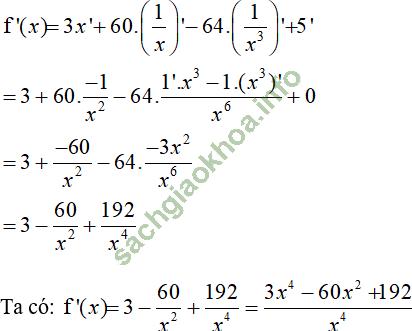
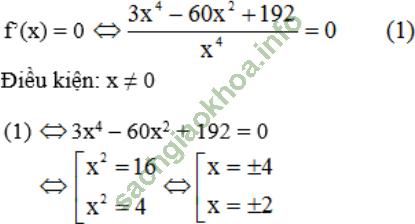
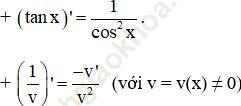
Giải bài 6 trang 176 sgk Đại Số 11:
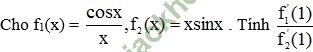
Bài giải:
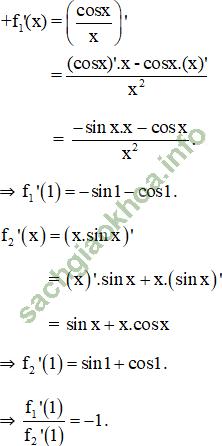
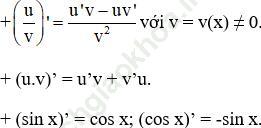
Giải bài 7 trang 176 sgk Đại Số 11: Viết phương trình tiếp tuyến của:
a) Hypebol 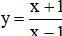 tại điểm A (2; 3).
tại điểm A (2; 3).
b) Đường cong y = x3 + 4x2 – 1 tại điểm có hoành độ x0 = -1.
c) Của parabol y = x2 – 4x + 4 tại điểm có tung độ y0 = 1.
Bài giải:


+ Phương trình tiếp tuyến của đường cong y = f (x) tại điểm M (x0; y0):![]()
Trong đó y0 = f (x0).
Giải bài 8 trang 177 sgk Đại Số 11: Cho chuyển động thẳng xác định bởi phương trình S = t3 – 3t2 – 9t, trong đó t được tính bằng giây (s) và S được tính bằng mét (m).
a. Tính vận tốc của chuyển động khi t = 2s.
b. Tính gia tốc của chuyển động khi t = 3s.
c. Tính gia tốc tại thời điểm vận tốc triệt tiêu.
d. Tính vận tốc tại thời điểm gia tốc triệt tiêu.
Bài giải:
Vận tốc: v (t) = S’ (t) = (t3 – 3t2 – 9t)' = 3t2 – 6t – 9.
Gia tốc: a (t) = v’ (t) = (3t2 – 6t – 9)’ = 6t – 6.
a) Khi t = 2s, v (2) = 3.22 – 6.2 – 9 = -9 (m/s).
b) Khi t = 3s, a (3) = 6.3 – 6 = 12 (m/s2).
c) v (t) = 0 ⇔ 3t2 – 6t – 9 = 0 ⇔ t = 3 (vì t > 0).
Khi đó a (3) = 12 m/s2.
d) a (t) = 0 ⇔ 6t – 6 = 0 ⇔ t = 1.
Khi đó v (1) = 3.12 – 6.1 – 9 = -12 (m/s).
Kiến thức áp dụng:+ Trong chuyển động thẳng, vận tốc tức thời là đạo hàm của hàm số s = s (t).
v’ (t0) = s’ (t0).
+ Gia tốc tức thời của chuyển động là đạo hàm cấp hai của hàm số s = s (t).
a (t0) = s’’ (t0) = v’ (t0).
Giải bài 9 trang 177 sgk Đại Số 11:
Cho hai hàm số 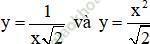
Viết phương trình tiếp tuyến với đồ thị của mỗi hàm số đã cho tại giao điểm của chúng. Tính góc giữa hai tiếp tuyến kể trên.
Bài giải:
Phương trình hoành độ giao điểm của hai hàm số là:
![]()
Thay x = 1 vào trong hai hàm số ta có 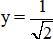
⇒ Tọa độ giao điểm 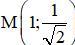

+ Góc giữa hai đường tiếp tuyến.
Tích hệ số góc của hai đường tiếp tuyến bằng: 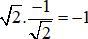
⇒ Hai tiếp tuyến vuông góc với nhau
⇒ Góc giữa hai tiếp tuyến bằng 90º.
Kiến thức áp dụng:+ Phương trình tiếp tuyến của đường cong y = f (x) tại điểm M (x0; y0):
trong đó y0 = f (x0).
+ Hai đường thẳng có tích của hệ số góc k1.k2 = -1 thì vuông góc với nhau.
Bài 10 (trang 177 SGK Đại số 11):
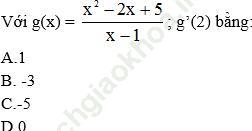
Bài giải:
Đáp án đúng là: B.
Giải thích:
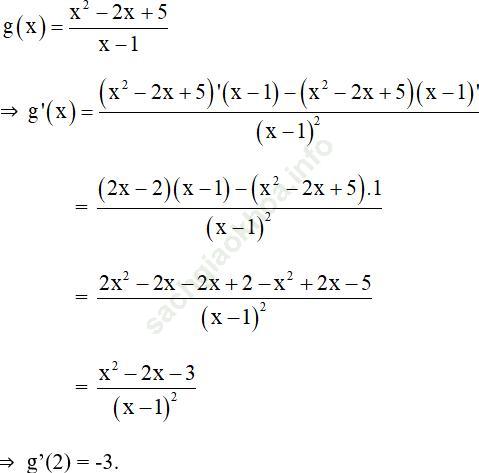
Bài 11 (trang 177 SGK Đại số 11):
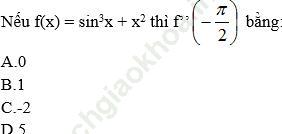
Bài giải:
Đáp án đúng là: D.
Giải thích:
f (x) = sin3x + x2
⇒ f' (x) = 3sin2x. (sinx)' + 2x = 3sin2x. cosx + 2x
⇒ f'' (x) = (3sin2x. cosx)' + (2x)'
= 3 (sin2x)'. cosx + 3sin2x (cosx)' + 2
= 3.2. sinx. cosx. cosx + 3sin2x. (-sinx) + 2
= 6sinx. cos2x - 3sin3x + 2
⇒ f'' (-π /2) = 5
Bài 12 (trang 177 SGK Đại số 11):

Bài giải:
Đáp án đúng là: C.
Giải thích:
Ta có:
h' (x) = 15 (x + 1)2 + 4
h'' (x) = 30 (x + 1);
h" (x) = 0 ⇔ 30 (x + 1) = 0 ⇔ x = -1
Bài 13 (trang 177 SGK Đại số 11):

Bài giải:
Đáp án đúng là: A.
Giải thích:
Ta có: f’ (x) = x2 + x + 1 =
Do đó phương trình f’ (x) ≤ 0 vô nghiệm