Bài 8: Phép đồng dạng - Giải BT Toán 11

Bài 8: Phép đồng dạng

Trả lời câu hỏi Toán 11 Hình học Bài 8 trang 30: Chứng minh nhận xét 2.

Phép vị tự tỉ số k là phép đồng dạng tỉ số |k|.

Bài giải:

Phép vị tự tâm O, tỉ số k biến điểm M, N thành 2 điểm M', N' sao cho OM'→ = kOM→

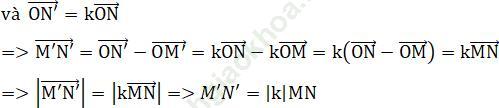
Vậy phép vị tự tỉ số k là phép đồng dạng tỉ số |k|.

Trả lời câu hỏi Toán 11 Hình học Bài 8 trang 30: Chứng minh nhận xét 3.

Nếu thực hiện liên tiếp phép đồng dạng tỉ số k và phép đồng dạng tỉ số p ta được phép đồng dạng tỉ số pk.

Bài giải:

- Phép đồng dạng tỉ số k biến 2 điểm M, N thành 2 điểm M', N' sao cho M'N' = kMN

- Phép đồng dạng tỉ số b biến 2 điểm M', N' thành 2 điểm M'', N''sao cho M''N'' = pM'N'

⇒ M''N'' = pkMN

Vậy: Nếu thực hiện liên tiếp phép đồng dạng tỉ số k và phép đồng dạng tỉ số p ta được phép đồng dạng tỉ số pk

Trả lời câu hỏi Toán 11 Hình học Bài 8 trang 31: Chứng minh tính chất a.

Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm ấy.

Bài giải:

Phép đồng dạng tỉ số k biến 3 điểm A, B, C thẳng hàng thành 3 điểm A', B', C' sao cho:

A'B' = kAB, B'C' = kBC, A'C' = kAC

A, B, C thẳng hàng và B nằm giữa A, C ⇔ AB + BC = AC

Do đó kAB + kBC = kAC hay A'B' + B'C' = A'C'

⇒ A', B', C' thẳng hàng và B' nằm giữa A', C'

Trả lời câu hỏi Toán 11 Hình học Bài 8 trang 31: Gọi A’, B’ lần lượt là ảnh của A, B qua phép đồng dạng F, tỉ số k. Chứng minh rằng nếu M là trung điểm của AB thì M’ = F (M) là trung điểm của A’B’.

Bài giải:

A’, B’ lần lượt là ảnh của A, B qua phép đồng dạng F, tỉ số k ⇒ A’B’= kAB

M’ = F (M) ⇒ A’M’ = kAM

M là trung điểm AB ⇒ AM = 1/2 AB ⇒ kAM = 1/2 kAB hay A’M’= 1/2 A’B’

Vậy M’ là trung điểm của A’B’

Trả lời câu hỏi Toán 11 Hình học Bài 8 trang 33: Hai đường tròn (hai hình vuông, hai hình chữ nhật) bất kì có đồng dạng với nhau không?

Bài giải:

Hai đường tròn (hai hình vuông, hai hình chữ nhật) bất kì có đồng dạng với nhau

Giải bài 1 trang 33 sgk Hình học 11: Cho tam giác ABC. Dựng ảnh của nó qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm B có tỉ số ½ và phép đối xứng qua đường trung trực của BC.

Bài giải:

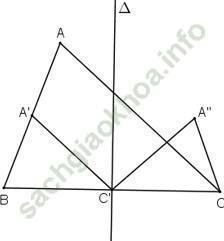
• ΔABC qua phép vị tự tâm B, tỉ số 1/2:

• ΔA’BC’ qua phép đối xứng trục Δ (Δ là trung trực của BC).

ĐΔ (A’) = A” (như hình vẽ).

ĐΔ (B) = C

ĐΔ (C’) = C’.

Vậy ảnh của tam giác ABC thu được sau khi thực hiện phép vị tự tâm B tỉ số 1/2 và phép đối xứng qua Δ là ΔA’’C’C.

Kiến thức áp dụng:

Giải bài 2 trang 33 sgk Hình học 11 (Phép đồng dạng): Cho hình chữ nhật ABCD, AC và BD cắt nhau tại I. Gọi H, K, L, J lần lượt là trung điểm của AD, BC, KC và IC. Chứng minh rằng hai hình thang JLKI và IHDC đồng dạng với nhau.

Bài giải:

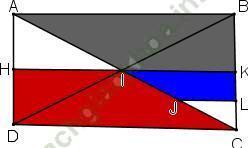
+ I là trung điểm AC; BD; HK

⇒ ĐI(H) = K; ĐI(D) = B; ĐI (C) = A.

⇒ Hình thang IKBA đối xứng với hình thang IHDC qua I (1)

+ J; L; K; I lần lượt là trung điểm của CI; CK; CB; CA

⇒ Hình thang JLKI là ảnh của hình thang IKBA qua phép vị tự tâm C tỉ số 1/2.

⇒ Hình thang JLKI là ảnh của hình thang IHDC qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng tâm I và phép vị tự tâm C tỉ số 1/2.

⇒ IJKI và IHDC đồng dạng.

Kiến thức áp dụng:

Giải bài 3 trang 33 sgk Hình học 11: Trong mặt phẳng Oxy cho điểm I (1; 1) và đường tròn tâm I bán kính 2. Viết phương trình đường tròn là ảnh của đường tròn trên qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc 45o và phép vị tự tâm O, tỉ số căn 2.

Bài giải:

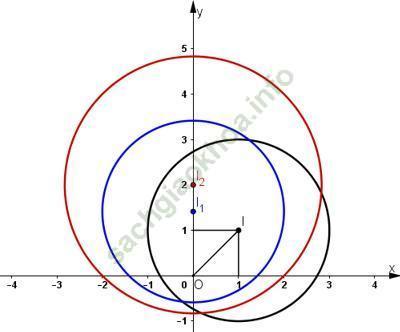
+ Gọi (I1; R1) = Q(O; 45º) (I; R) (Phép quay đường tròn tâm I, bán kính R qua tâm O một góc 45º).

Kiến thức áp dụng:

Giải bài 4 trang 33 sgk Hình học 11: Cho tam giác ABC vuông tại A, AH là đường cao kẻ từ A, tìm một phép đồng dạng biến tam giác HBA thành tam giác ABC.

Bài giải:

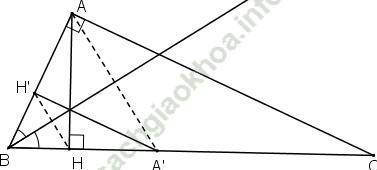
Gọi d là đường phân giác của góc B của ΔABC.

+ Phép đối xứng qua d: biến H thành H’ ∈ AB, biến A thành A’ ∈ BC; biến B thành B

(Dễ dàng nhận thấy H’ ∈ BA; A’ ∈ BC).

⇒ ΔH’BA’ = Đd(ΔHBA).

⇒ ΔH’BA’ = ΔHBA.

Mà ΔABC ΔHBA theo tỉ số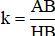

⇒ ΔABC ΔH’BA’ theo tỉ số k

⇒ AB = k. H’B; BC = k. BA’.

Mà A ∈ tia BH’; C ∈ tia BA’

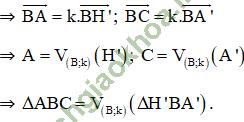
Vậy phép đồng dạng cần tìm là phép vị tự tâm B, tỉ số 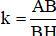hợp với phép đối xứng trục d là phân giác của

Kiến thức áp dụng: Bài trước: Bài 7: Phép vị tự - Giải BT Toán 11 Bài tiếp: Câu hỏi ôn tập chương 1 - Giải BT Toán 11