Ôn tập chương 4 - Giải BT Toán 11
Ôn tập chương 4
Bài 1 (trang 141 SGK Đại số 11): Hãy lập bảng liệt kê các giới hạn đặc biệt của dãy số và giới hạn đặc biệt của hàm số.
Bài giải:
Giải bài 2 trang 141 sgk Đại Số 11 Ôn tập: Cho hai dãy số (un) và (vn). Biết |un – 2| ≤ vn với mọi n và lim vn = 0. Có kết luận gì về giới hạn của dãy số (un)?
Lấy số dương ε bé tùy ý bất kì:
⇒ có một số n0 thỏa mãn: |vn| < ε kể từ n = n0.
⇒ |un – 2| < vn < |vn| < ε kể từ n = n0 trở đi
⇒ lim (un – 2) = 0
⇒ lim un = 2.
Dãy số (un) có lim un = 0 nếu |un| có thể nhỏ hơn 1 số dương bé tùy ý kể từ một số hạng nào đó trở đi.
Bài 3 (trang 141 SGK Đại số 11 Ôn tập): Tên một học sinh được mã hóa bởi số 1530. Biết rằng mỗi chữ số trong số này là giá trị một trong các biểu thức A, H, N, O với
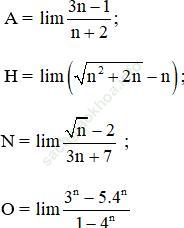
Hãy cho biết tên của học sinh này, bằng cách thay các chữ số trên bởi các chữ kí hiệu biểu thức tương ứng.
Bài giải: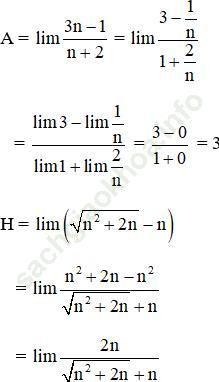
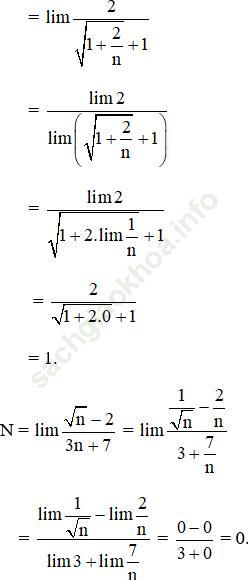
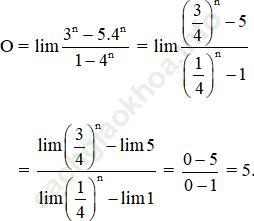
Khi thay đổi chữ số 1530 bởi các biểu thức giới hạn tương ứng ta được chữ HOAN là tên các bạn học sinh đã cho.
Bài 4 (trang 142 SGK Đại số 11):
a. Có nhận xét gì về công bội của các cấp số nhân lùi vô hạn?
b. Cho ví dụ về một cấp số nhân lùi vô hạn và có công bội là số âm và một cấp số nhân lùi vô hạn có công bội là số dương và tính tổng của các cấp số nhân đó.
Bài giải:a) Cấp số nhân vô hạn với công bội q mà |q| < 1 là cấp số nhân lùi vô hạn
b) Ví dụ về cấp số nhân lùi vô hạn có công bội âm:
Giải bài 5 trang 142 sgk Đại Số 11: Tìm các giới hạn sau:
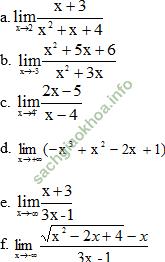
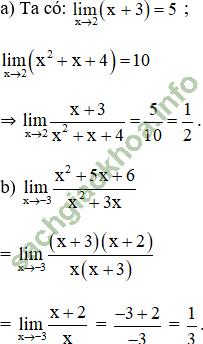
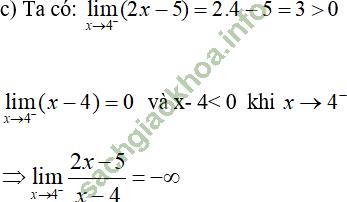
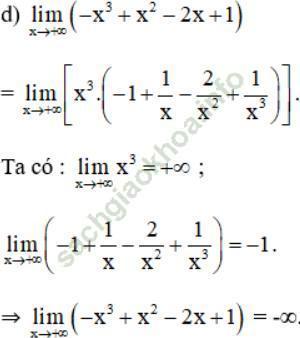
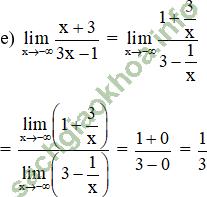
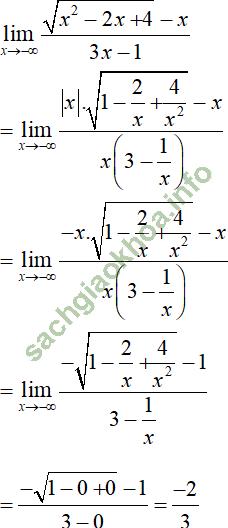
Giả sử có: 
+ Nếu L, M là số hữu hạn, M ≠ 0 thì 
+ Nếu L hữu hạn, M = ±∞ thì 
+ Nếu L = ∞; M hữu hạn, M ≠ 0 thì 
khi f (x) và g (x) cùng dấu;
khi f (x) và g (x) trái dấu.
+ Nếu L hữu hạn, M = 0 thì 
khi f (x) và g (x) cùng dấu;
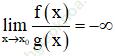khi f (x) và g (x) trái dấu.Giải bài 6 trang 142 sgk Đại Số 11:
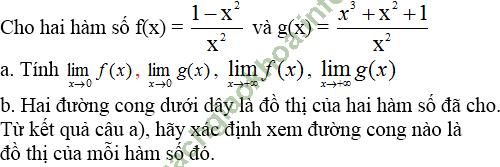
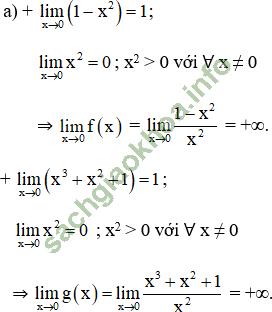
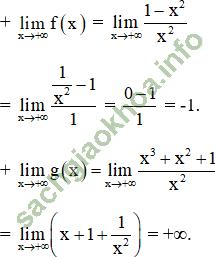
b) Nhận thấy hình a) khi x → +∞ thì y → +∞
⇒ Hình a) là đồ thị hàm số y = g (x).
Hình b) khi x → +∞ thì y → -1
⇒ Hình b) là đồ thị hàm số y = f (x).
+ Khi 
thì ta có:
Nếu 
và g (x) cùng dấu thì 
Nếu 
và g (x) trái dấu thì 
Giải bài 7 trang 143 sgk Đại Số 11: Xét tính liên tục trên R của hàm số:
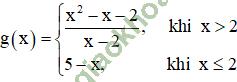
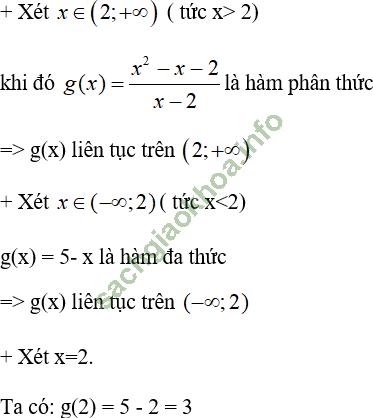
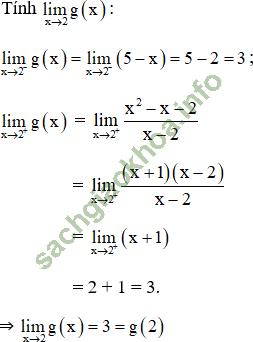
⇒ g (x) liên tục tại 2.
Vậy hàm số g (x) liên tục trên R.
+ Hàm số f (x) liên tục tại x0 nếu 
+ Hàm đa thức liên tục trên R, hàm phân thức liên tục trên từng khoảng xác định của chúng.
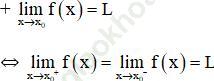
Giải bài 8 trang 143 sgk Đại Số 11: Chứng minh rằng phương trình x5 – 3x4 + 5x – 2 = 0 có ít nhất ba nghiệm nằm trong khoảng (-2; 5)
Đặt f (x) = x5 – 3x4 + 5x – 2
f (x) là hàm đa thức nên liên tục trên R.
Ta có: f (0) = –2 < 0
f (1) = 1 > 0
f (2) = -8 < 0
f (3) = 13 > 0
⇒ f (0).f (1) < 0; f (1).f (2) < 0; f (2).f (3) < 0
⇒ Phương trình f (x) = 0 có ít nhất 1 nghiệm thuộc khoảng (0; 1); 1 nghiệm thuộc khoảng (1; 2); 1 nghiệm thuộc khoảng (2; 3)
⇒ f (x) = 0 có ít nhất 3 nghiệm thuộc (0; 3) hay f (x) = 0 có ít nhất 3 nghiệm thuộc (-2; 5).
Nếu hàm số y = f (x) liên tục trên đoạn [a; b] và f (a).f (b) < 0 thì tồn tại ít nhất 1 điểm c ∈ (a; b) sao cho f (c) = 0.
Bài 9 (trang 143 SGK Đại số 11): Mệnh đề nào sau đây là mệnh đề đúng?
A. Một dãy số có giới hạn thì luôn luôn tăng hoặc luôn luôn giảm.
B. Nếu (un) là dãy số tăng thì lim un = + ∞.
C. Nếu lim un = + ∞ và lim vn = + ∞ thì lim (un – vn) = 0
D. Nếu un = an và – 1 < a < 0 thì lim un = 0.
Bài giải:Đáp án đúng là: D.
Giải thích:
Bài 10 (trang 143 SGK Đại số 11):
Bài giải:
Đáp án đúng là: B.
Giải thích:
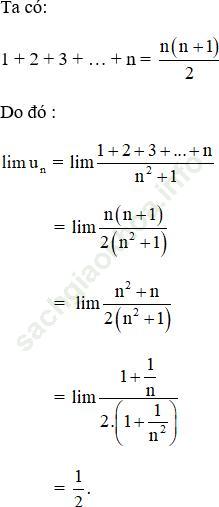
Bài 11 (trang 143 SGK Đại số 11):
Bài giải:
Đáp án đúng là: C.
Giải thích:
un là tổng n số hạng đầu tiên của CSN có số hạng đầu u1 = √2, công bội q = √2.
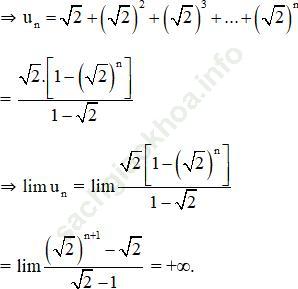
+ Lưu ý: Đây không phải tổng của CSN lùi vô hạn vì công bội q > 1 nên không thể áp dụng công thức tổng của CSN lùi vô hạn.
Bài 12 (trang 144 SGK Đại số 11):
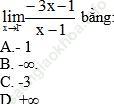
Bài giải:
Bài 13 (trang 144 SGK Đại số 11):
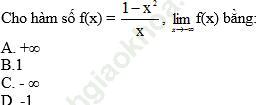
Bài giải:
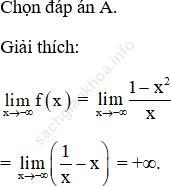
Bài 14 (trang 144 SGK Đại số 11): Cho hàm số:
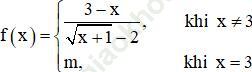
Hàm số đã cho liên tục tại x = 3 khi m bằng:
A. 4
B. -1
C. 1
D. -4
Bài giải:Đáp án đúng là: D.
Giải thích:
Ta có:
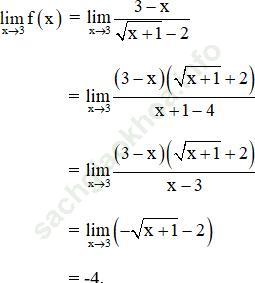
Bài 15 (trang 144 SGK Đại số 11): Cho phương trình -4x3 + 4x- 1 = 0 (1)
Mệnh đề sai:
Bài giải:
Đáp án đúng là: B.
Giải thích:
Đặt f (x) = -4x3 + 4x – 1.
+ f (x) là hàm đa thức nên liên tục trên R ⇒ A đúng.
+ f (-2) = 23; f (1) = -1
⇒ f (-2).f (1) < 0
⇒ f (x) có ít nhất 1 nghiệm nằm trong khoảng (-2; 1) ⊂ (-∞; 1).
⇒ B sai.
+ f (0) = -1
⇒ f (-2).f (0) < 0
⇒ f (x) có ít nhất 1 nghiệm nằm trong khoảng (-2; 0).
⇒ C đúng.
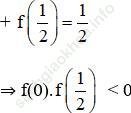
⇒f (x) có ít nhất 1 nghiệm nằm trong khoảng 
Kết hợp với C ⇒ f (x) có ít nhất 2 nghiệm nằm trong khoảng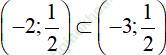 
⇒ D đúng.