Bài 2: Giới hạn của hàm số - Giải BT Toán 11
Bài 2: Giới hạn của hàm số
Trả lời câu hỏi Toán 11 Đại số Bài 2 trang 123: Xét hàm số: 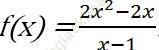
1. Cho biến x những giá trị khác 1 lập thành dãy số xn, xn → 1 như trong bảng sau:
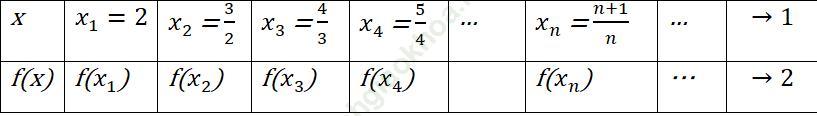
Khi đó, các giá trị tương ứng của hàm số: f (x1), f (x2), …, f (xn), … cũng lập thành một dãy số mà ta kí hiệu là f (xn).
a) Chứng minh rằng f (xn) = 2xn = (2n + 2)/n.
b) Tìm giới hạn của dãy số f (xn).
2. Chứng minh rằng với dãy số bất kì xn, xn ≠ 1 và xn → 1, ta luôn có f (xn) → 2.
(Với tính chất thể hiện trong câu 2, ta nói hàm số 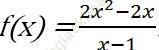 có giới hạn là 2 khi x dần tới 1).
có giới hạn là 2 khi x dần tới 1).
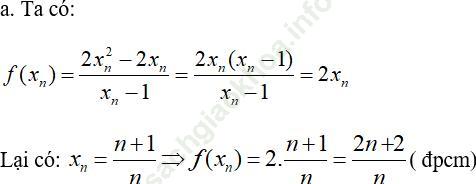
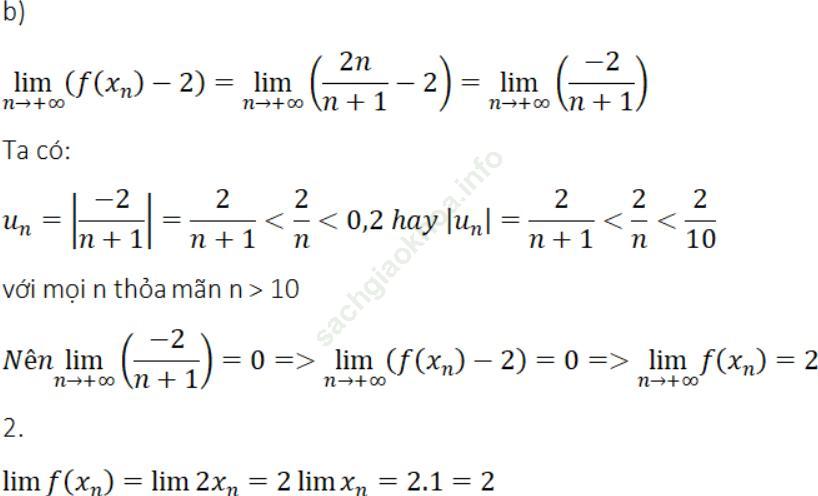
Trả lời câu hỏi Toán 11 Đại số Bài 2 trang 127: Trong biểu thức (1) xác định hàm số y = f (x) ở Ví dụ 4, cần thay 2 bằng số nào để hàm số có giới hạn là -2 khi x → 1?
Bài giải:
Cần thay 2 bằng 7 để hàm số có giới hạn là -2 khi x → 1
Trả lời câu hỏi Toán 11 Đại số Bài 2 trang 127: Cho hàm số f (x) = 1/ (x-2) có đồ thị như ở Hình 52
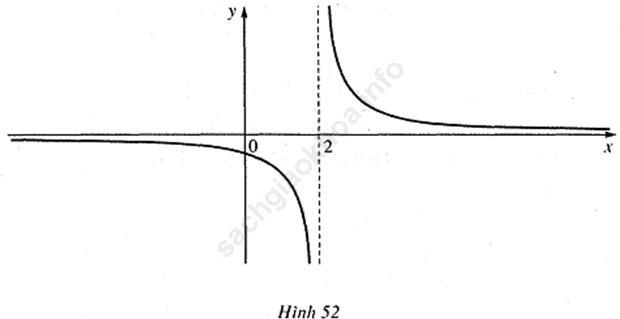
Quan sát đồ thị và cho biết:
- Khi biến x dần tới dương vô cực, thì f (x) dần tới giá trị nào.
- Khi biến x dần tới âm vô cực, thì f (x) dần tới giá trị nào.
Bài giải:
- Khi biến x dần tới dương vô cực, thì f (x) dần tới giá trị 0.
- Khi biến x dần tới âm vô cực, thì f (x) dần tới giá trị 0.
Giải bài 1 trang 132 sgk Đại Số 11: Dùng định nghĩa tìm các giới hạn sau:
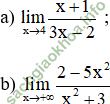
Bài giải:
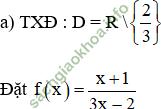
Lấy dãy (xn) bất kì; xn ∈ D; lim xn = 4.

b) TXĐ: D = R.
![]()
Lấy dãy (xn) bất kì thỏa mãn xn → +∞
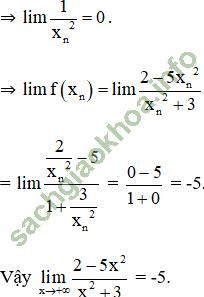
+ Định nghĩa giới hạn của hàm số y = f (x) tại điểm x = x0
![]()
+ Định nghĩa giới hạn của hàm số y = f (x) tại vô cùng.
Giải bài 2 trang 132 sgk Đại Số 11: Cho hàm số:
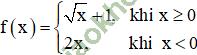
và các dãy số (un) với 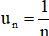 ; (vn) với
; (vn) với 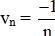
Tính limun, limvn, limf (un), limf (vn).
Từ đó có kết luận gì về giới hạn của hàm số đã cho khi x → 0?
Bài giải:

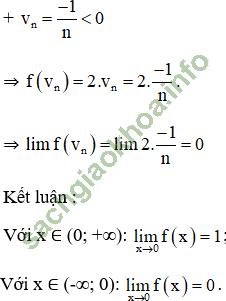
Giải bài 3 trang 132 sgk Đại Số 11: Tính các giới hạn sau:
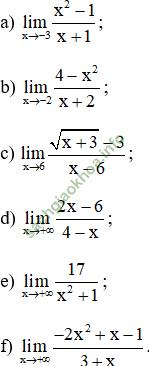
Bài giải:
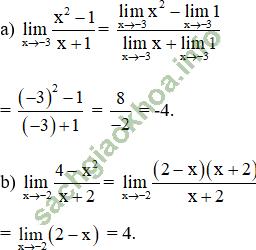
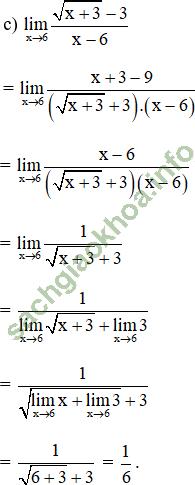
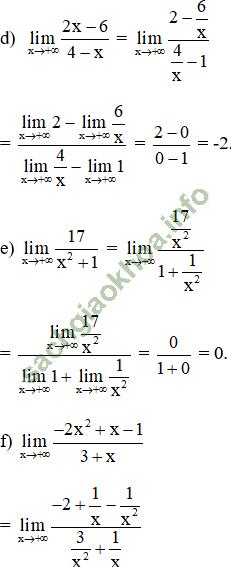
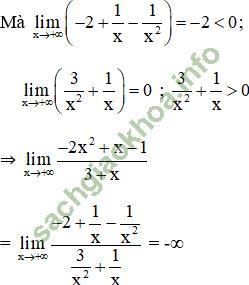
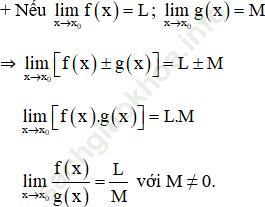
+ Đối với trường hợp M = 0, L ≠ 0 thì ![]() nếu f (x) và g (x) cùng dấu;
nếu f (x) và g (x) cùng dấu;
+ Đối với trường hợp f (x0) = g (x0) = 0 (L = M = 0)
⇒ phân tích được f (x) = (x – x0)k.q (x); g (x) = (x – x0)h.p (x)
⇒ Rút gọn (x – x0)k hoặc (x – x0)h để đưa về 1 trong 2 trường hợp trên.
Giải bài 4 trang 132 sgk Đại Số 11: Tìm các giới hạn sau:
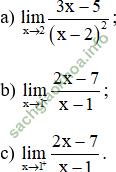
Bài giải:
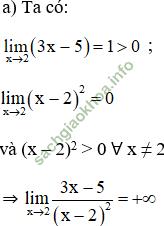
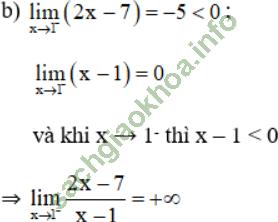
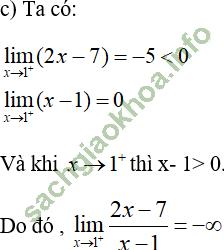
Khi ![]() thì ta có:
thì ta có:
+ Nếu ![]() và g (x) cùng dấu thì
và g (x) cùng dấu thì ![]()
+ Nếu ![]() và g (x) trái dấu thì
và g (x) trái dấu thì ![]()
Giải bài 5 trang 133 sgk Đại Số 11: Cho hàm số: 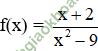
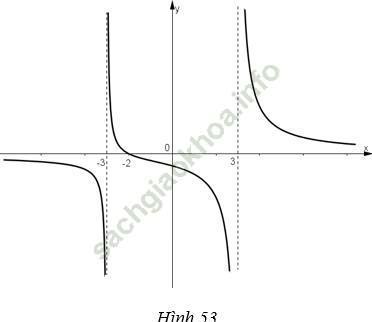
a. Quan sát đồ thị và nêu nhận xét về giá trị hàm số cho khi:
x →- ∞, x →3-,x →-3+
b. Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau:

Bài giải:
a) Quan sát đồ thị nhận thấy:
f (x) → 0 khi x → -∞
f (x) → -∞ khi x → 3-
f (x) → +∞ khi x → (-3)+.
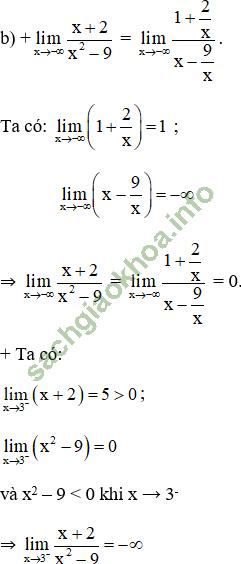
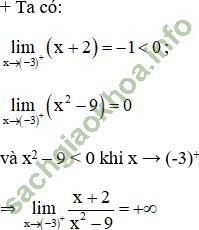
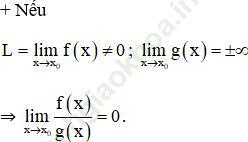
+ Khi ![]() thì ta có:
thì ta có:
+ Nếu ![]() và g (x) cùng dấu thì
và g (x) cùng dấu thì ![]()
+ Nếu ![]() và g (x) trái dấu thì
và g (x) trái dấu thì ![]()
Giải bài 6 trang 133 sgk Đại Số 11: Tính:
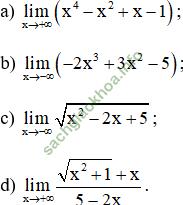
Bài giải:
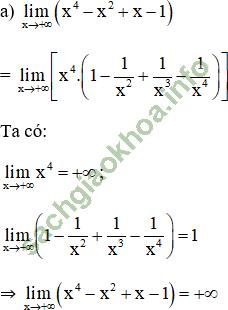
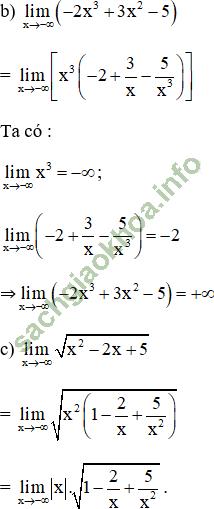
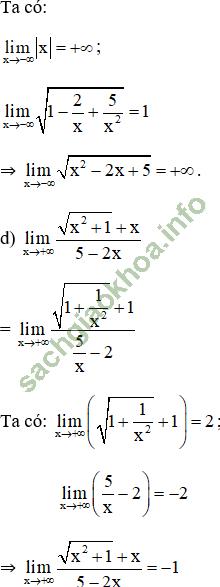
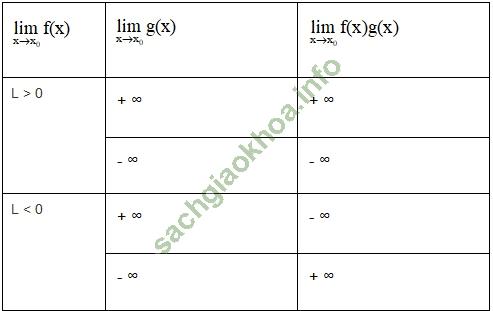
Quy tắc tìm giới hạn của tích f (x).g (x)
Nếu ![]() = L ≠ 0 và
= L ≠ 0 và ![]() = + ∞ (hoặc -∞) thì
= + ∞ (hoặc -∞) thì ![]() được tính theo quy tắc trong bảng sau:
được tính theo quy tắc trong bảng sau:
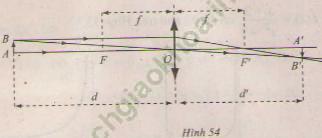
Giải bài 7 trang 133 sgk Đại Số 11: Một thấu kính hội tụ có tiêu cự là f. Gọi d và d' lần lượt là khoảng cách từ một vật thật AB và ảnh A'B' của nó tới quang tâm O của thấu kính (hình dưới).
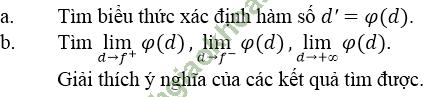
Bài giải:
a) Thấu kính hội tụ có tiêu cự f
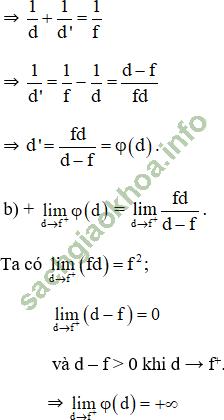
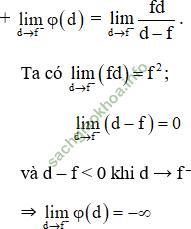
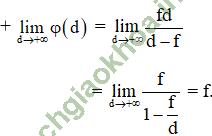
+ Đối với thấu kính hội tụ ta luôn có công thức liên hệ giữa khoảng cách từ vật, ảnh đến quang tâm và tiêu cự là: ![]()
+ Khi ![]() thì ta có:
thì ta có:
+ Nếu ![]() và g (x) cùng dấu thì
và g (x) cùng dấu thì ![]()
+ Nếu ![]() và g (x) trái dấu thì
và g (x) trái dấu thì ![]()