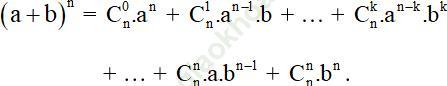Bài 3: Nhị thức Niu-tơn - Giải BT Toán 11
Bài 3: Nhị thức Niu-tơn
Trả lời câu hỏi Toán 11 Đại số Bài 3 trang 55: Khai triển biểu thức (a + b)4 thành tổng các đơn thức.
Bài giải:(a + b)4 = (a + b)3(a + b)
= (a3 + 3a2b + 3ab2 + b3) (a + b)
= a4 + 3a3b + 3a2b2 + ab3 + a3b + 3a2b2 + 3ab3 + b4
= a4 + 4a3b + 6a2b2 + 4ab3 + b4
Trả lời câu hỏi Toán 11 Đại số Bài 3 trang 57: Dùng tam giác Pa-xcan, chứng tỏ rằng:
a) 1 + 2 + 3 + 4 = C25;
b) 1 + 2 + … + 7 = C28.
Bài giải:a) Dựa vào tam giác Pa-xcan: C14 = 4; C24 = 6
C25 = C14 + C24 = 4 + 6 = 10
Mà: 1 + 2 + 3 + 4 = 10
⇒ 1 + 2 + 3 + 4 = C25
b)Dựa vào tam giác Pa-xcan: C17 = 7; C27 = 21
C28 = C17 + C27 = 7 + 21 = 28
1 + 2 +⋯+ 7 = ((1 + 7).7)/2 = 28
⇒ 1 + 2 +⋯+ 7 = C28
Giải bài 1 trang 57 sgk Đại số 11: Viết khai triển theo công thức nhị thức Niu – tơn:
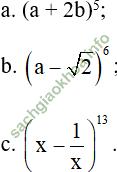
Bài giải:
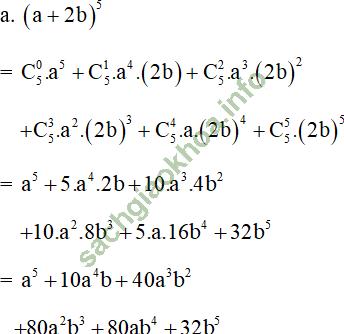
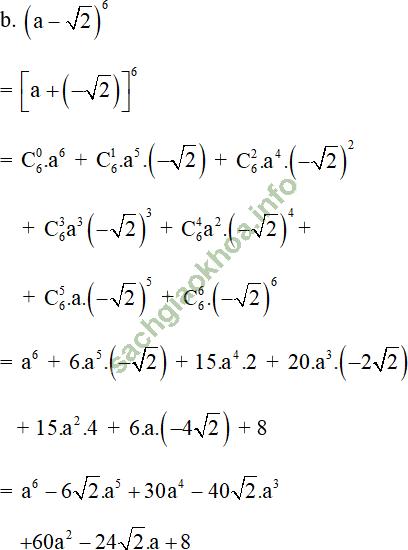
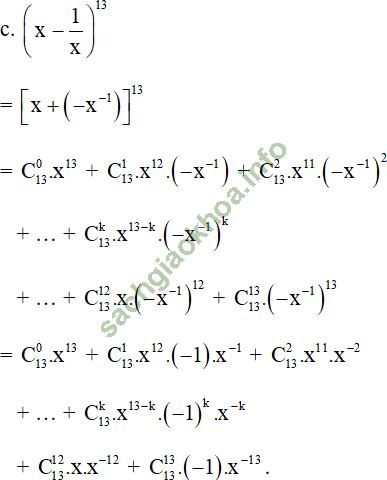
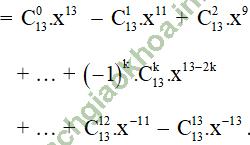
+ Khai triển nhị thức Niu-tơn:
Giải bài 2 trang 58 sgk Đại số 11: Tìm hệ số của x3 trong khai triển của biểu thức:
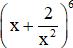
Bài giải:
+ Số hạng tổng quát của khai triển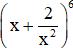
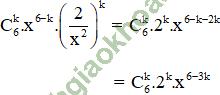
+ x3 ứng với 6 – 3k = 3 ⇔ k = 1.
Vậy hệ số của x3 là: 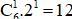
Bài 3 (trang 58 SGK Đại số 11): Biết hệ số của x2 trong khai triển của (1 – 3x)n là 90. Tìm n.
Bài giải:+ Số hạng tổng quát của khai triển (1 – 3x)n là: ![]()
+ Số hạng chứa x2 ứng với k = 2.
Hệ số của x2 là 90 nên ta có:
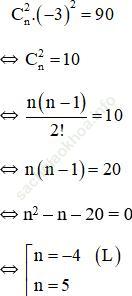
Vậy n = 5.
Giải bài 4 trang 58 sgk Đại số 11: Tìm số hạng không chứa x trong khai triển của 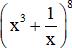
+ Số hạng tổng quát trong khai triển 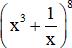
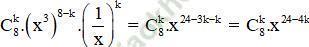
+ Số hạng không chứa x tương ứng với 24 – 4k = 0 ⇔ k = 6.
Vậy số hạng không chứa x trong khai triển đã cho là: 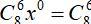
Với các bài toán liên quan đến hệ số của xm trong khai triển một biểu thức ta thường làm như sau:
+ Tìm số hạng tổng quát trong khai triển.
+ Tìm k tương ứng với xm
+ Tìm hệ số của xm tương ứng với k vừa tìm được.
Giải bài 5 trang 58 sgk Đại số 11: Tìm khai triển biểu thức (3x – 4)17 thành đa thức, hãy tính tổng các hệ số của đa thức nhận được.
Bài giải:
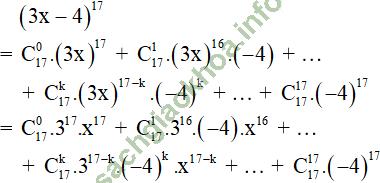
Đặt S là tổng các hệ số của đa thức khai triển.
Ta có:
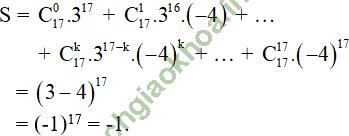
Vậy tổng các hệ số của đa thức khai triển bằng -1.
+ Khai triển nhị thức Niu-tơn:
Giải bài 6 trang 58 sgk Đại số 11: Chứng minh rằng:
a) 1110 – 1 chia hết cho 100
b) 101100 – 1 chia hết cho 10.000
c) 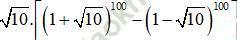 là một số nguyên
là một số nguyên
Bài giải:
a) Ta có; 1110 = (10+1)10 (khai triển nhị thức Niu- tơn)
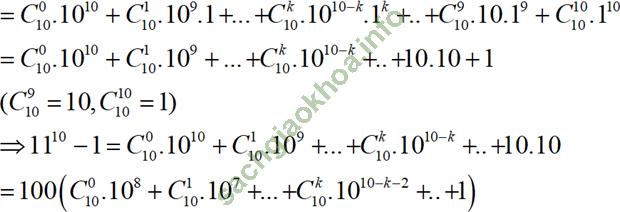
Do đó, 1110 -1 chia hết cho 100
b) Ta có: 10110 = (100+1)10 (khai triển nhị thức Niu- tơn)
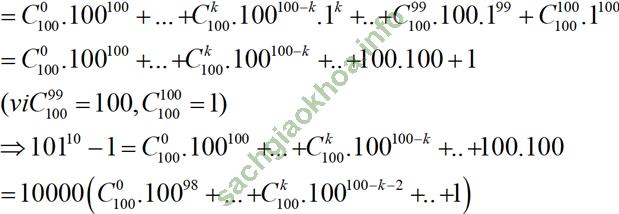
Do đó, 10110 -1 chia hết cho 10000

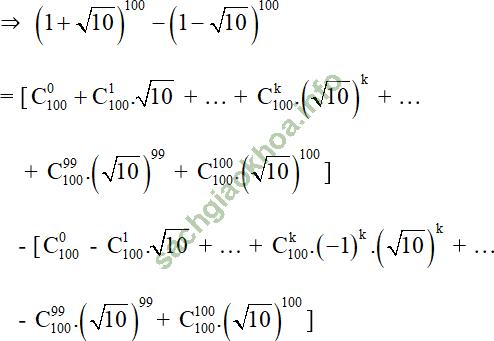
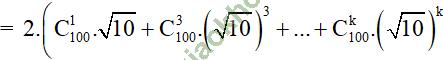

+ Khai triển nhị thức Niu-tơn: