Bài 3: Phép đối xứng trục - Giải BT Toán 11
Bài 3: Phép đối xứng trục
Trả lời câu hỏi Toán 11 Hình học Bài 3 trang 9: Cho hình thoi ABCD (h. 1.12). Tìm ảnh của các điểm A, B, C, D qua phép đối xứng trục AC.
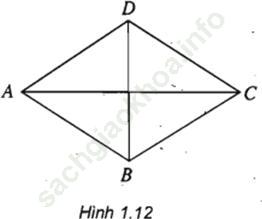
Bài giải:
Qua phép đối xứng trục AC
ảnh của A là A
ảnh của B là D
ảnh của C là C
ảnh của D là B
Trả lời câu hỏi Toán 11 Hình học Bài 3 trang 9: Chứng minh nhận xét 2.
M’ = Đd(M)⇔ M = Đd(M')
Bài giải:
M'= Đd(M)nghĩa là phép biến hình này biến mỗi điểm M thuộc d thành chính nó hoặc biến mỗi điểm M không thuộc d thành M' sao cho d là đường trung trực của đoạn thẳng MM’
- M ∈ d ⇒ M'= Đd(M) ≡ M ⇒ M = Đd(M')
- M ∉ d ⇒ M'= Đd(M) thì d là đường trung trực của MM’
⇒ M’∉ d và phép biến hình biến mỗi điểm M’thành M sao cho d là đường trung trực của đoạn thẳng M'M
⇒ M = Đd(M')
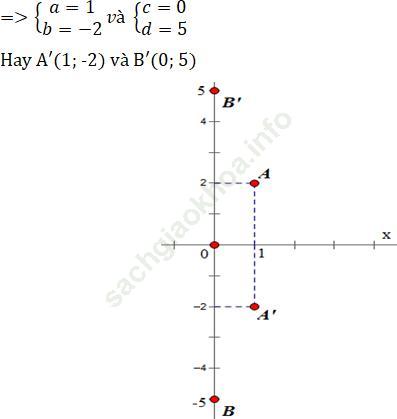
Trả lời câu hỏi Toán 11 Hình học Bài 3 trang 9: Tìm ảnh của các điểm A (1; 2), B (0; -5) qua phép đối xứng trục qua trục Ox.
Bài giải:
Gọi A' (a, b) và B' (c, d) lần lượt là ảnh của A và B qua phép đối xứng trục qua trục Ox
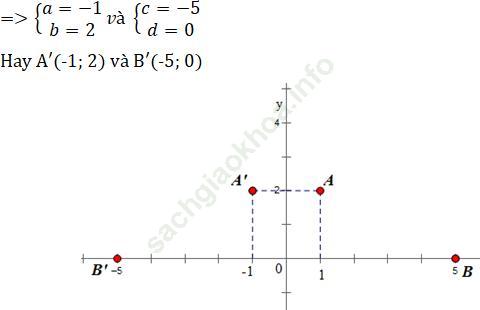
Trả lời câu hỏi Toán 11 Hình học Bài 3 trang 10: Tìm ảnh của các điểm A (1; 2), B (5; 0) qua phép đối xứng trục Oy.
Bài giải:
Gọi A' (a, b) và B' (c, d) lần lượt là ảnh của A và B qua phép đối xứng trục qua trục Oy
Trả lời câu hỏi Toán 11 Hình học Bài 3 trang 10: Chọn hệ tọa độ Oxy sao cho trục Ox trùng với trục đối xứng, rồi dùng biểu thức tọa độ của phép đối xứng qua trục Ox để chứng minh tính chất 1.
Bài giải:
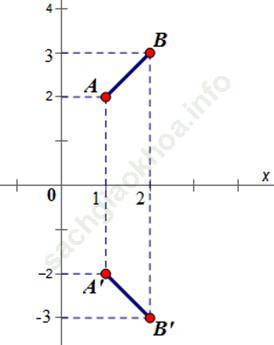
Lấy ảnh A', B' của hai điểm A (1; 2) và B (2; 3) qua phép đối xứng trục Ox
Dùng biểu thức tọa độ của phép đối xứng qua trục Ox, ta có:
A' (1; -2), B' (2; -3)
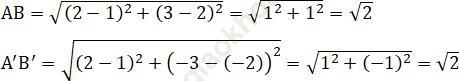
⇒ A'B' = AB
Trả lời câu hỏi Toán 11 Hình học Bài 3 trang 11:
a) Trong những chữ cái dưới đây, chữ nào là hình có trục đối xứng?

b) Tìm một số hình tứ giác có trục đối xứng.
Bài giải:a) Các chữ cái có trục đối xứng là: H; A; O; N
b) 1 số hình tứ giác có trục đối xứng là: hình chữ nhật, hình thoi, hình vuông
Giải bài 1 trang 11 sgk Hình học 11: Trong mặt phẳng Oxy cho A (1; -2) và B (3; 1). Tìm ảnh của A, B và đường thẳng AB qua phép đối xứng trục Ox.
Bài giải:
+ A’ (x1; y1) đối xứng với A (1; -2) qua trục Ox
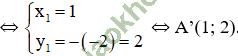
+ B’ (x2; y2) đối xứng với B (3; 1) qua trục Ox
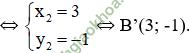
* Qua phép đối xứng trục Ox, biến điểm A và B lần lượt thành 2 điểm A’ và B’. Nên biến đường thẳng AB thành đường thẳng A’B’.
+ Đường thẳng A’B’ đi qua A’ (1; 2) và nhận vecto chỉ phương là A'B'→(2, -3) nên vecto pháp tuyến là: (3; 2)
Phương trình đường thẳng A’B’ là:
3 (x-1)+ 2 (y-2) = 0 hay 3x+ 2y- 7=0
Kiến thức áp dụng:+ M (x; y) đối xứng với M’ (x’; y’) qua Ox khi
Giải bài 2 trang 11 sgk Hình học 11: Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x – y + 2 = 0. Viết phương trình của đường thẳng d’ là ảnh của d qua phép đối xứng trục Oy.
Bài giải:
Gọi M (x; y) tùy ý thuộc d, suy ra 3x – y + 2 = 0 (1)
Gọi M’ (x’; y’) = ĐOy(M) ⇔ 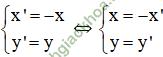
Thay vào (1), ta được: 3 (-x’) – y’ + 2 = 0 ⇔ 3x’ + y’ – 2 = 0
Do đó, điểm M’ thuộc đường thẳng d’: 3x + y – 2 = 0.
Vậy qua phép đối xứng trục Oy biến đường thẳng d thành đường thẳng d’: 3x + y- 2=0
Kiến thức áp dụng:+ M (x; y) đối xứng với M’ (x’; y’) qua Oy khi ![]()
Giải bài 3 trang 11 sgk Hình học 11: Trong các chữ cái sau, chữ nào là hình có trục đối xứng?
W
VIETNAM
O
Bài giải:
- W, V, E, T, A, M: Mỗi chữ cái là một hình có trục đối xứng.
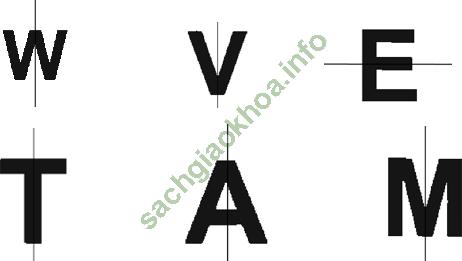
- Chữ I có hai trục đối xứng.
- Chữ O có vô số trục đối xứng là các đường thẳng đi qua tâm.
- Chữ N là hình không có trục đối xứng.
Kiến thức áp dụng:+ Đường thẳng d được gọi là trục đối xứng của hình H nếu phép đối xứng qua d biến H thành chính nó.