Bài 3: Một số phương trình lượng giác thường gặp - Giải BT Toán 11
Bài 3: Một số phương trình lượng giác thường gặp
Trả lời câu hỏi Toán 11 Đại số Bài 3 trang 29: Giải các phương trình trong ví dụ 1.
a) 2sinx – 3 = 0 là phương trình bậc nhất đối với sinx.
b) √ 3 tanx + 1 = 0 là phương trình bậc nhất đố với tanx.
Bài giải:a) 2sinx – 3 = 0 ⇔ sin x = 3/2, vô nghiệm vì |sinx| ≤ 1
b)√ 3tanx + 1 = 0 ⇔ tanx = (-√ 3)/3 ⇔ x = (-π)/6 + kπ, k ∈ Z
Trả lời câu hỏi Toán 11 Đại số Bài 3 trang 31: Giải các phương trình sau:
a) 3cos2x – 5cosx + 2 = 0;
b) 3tan2x - 2√ 3 tanx + 3 = 0.
Bài giải:a)3cos2x - 5 cos x + 2 = 0
Đặt cos x = t với điều kiện -1 ≤ t ≤ 1 (*),
ta được phương trình bậc hai theo t:
3t2 - 5t + 2 = 0 (1)
Δ = (-5)2 - 4.3.2 = 1
Phương trình (1)có hai nghiệm là:
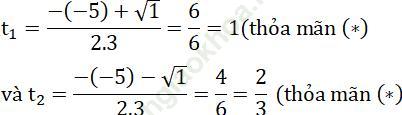
Ta có:
cosx = 1 ⇔ cosx = cos0
⇔ x = k2π, k ∈ Z
cosx = 2/3 ⇔ x = ± arccos 2/3 + k2π, k ∈ Z
b) 3tan2 x - 2√ 3 tanx + 3 = 0
Đặt tanx = t
ta được phương trình bậc hai theo t:
3t2 - 2√ 3 t + 3 = 0 (1)
Δ = (-2√ 3)2 - 4.3.3 = -24 < 0
Vậy Phương trình (1) vô nghiệm, nên không có x thỏa mãn đề bài
Trả lời câu hỏi Toán 11 Đại số Bài 3 trang 32: Hãy nhắc lại:
a) Các hằng đẳng thức lượng giác cơ bản;
b) Công thức cộng;
c) Công thức nhân đôi;
d) Công thức biến đổi tích thành tổng và tổng thành tích.
Bài giải:a) Các hằng đẳng thức lượng giác cơ bản:
sin2α + cos2α = 1
1 + tan2α = 1/ (cos2α); α ≠ π /2 + kπ, k ∈ Z
1 + cot2α = 1/ (sin2α); α ≠ kπ, k ∈ Z
tanα. cotα = 1; α ≠ kπ /2, k ∈ Z
b) Công thức cộng:
cos (a - b) = cosa cosb + sina sinb
cos (a + b) = cosa cosb - sina sinb
sin (a - b) = sina cosb - cosa sinb
sin (a + b) = sina. cosb + cosa. sinb
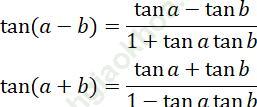
c) Công thức nhân đôi:
sin2α = 2 sinα cosα
cos2α = cos2α - sin2α = 2cos2α - 1 = 1 - 2sin2α
d) Công thức biến đổi tích thành tổng:
cos a cosb = 1/2 [cos (a - b) + cos (a + b)]
sina sinb = 1/2 [cos (a - b) - cos (a + b)]
sina cosb = 1/2 [sin (a - b) + sin (a + b)]
Công thức biến đổi tổng thành tích:
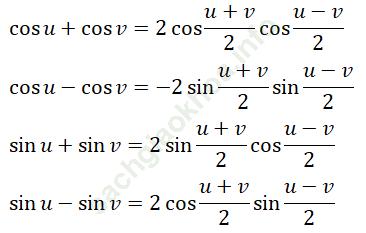
Trả lời câu hỏi Toán 11 Đại số Bài 3 trang 34: Giải phương trình 3cos2 6x + 8sin3x cos3x – 4 = 0.
Bài giải:3cos2 6x + 8sin3x cos3x - 4 = 0
⇔ 3 (1-sin26x)+ 4sin6x - 4 = 0
⇔ -3sin26x + 4sin6x - 1 = 0
Đặt sin6x = t với điều kiện -1 ≤ t ≤ 1 (*),
Ta được phương trình bậc hai theo t:
-3t2 + 4t - 1 = 0 (1)
Δ = 42 - 4. (-1). (-3) = 4
Phương trình (1) có hai nghiệm là:
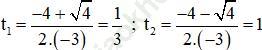 (thỏa mãn (*)
(thỏa mãn (*)Ta có:

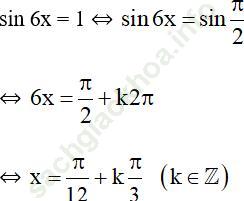
Trả lời câu hỏi Toán 11 Đại số Bài 3 trang 35: Dựa vào các công thức cộng đã học:
sin (a + b) = sina cosb + sinb cosa;
sin (a – b) = sina cosb - sinb cosa;
cos (a + b) = cosa cosb – sina sinb;
cos (a – b) = cosa cosb + sina sinb;
và kết quả cos π /4 = sinπ /4 = √ 2/2, hãy chứng minh rằng:
a) sinx + cosx = √ 2 cos (x - π /4);
b) sin x – cosx = √ 2 sin (x - π /4).
Bài giải:a) √ 2 cos (x - π/4)
= √ 2. (cosx. cos π/4 + sinx. sin π/4)
= √ 2. (√ 2/2. cosx + √ 2/2. sinx)
= √ 2. √ 2/2. cosx + √ 2. √ 2/2. sinx
= cosx + sinx (đpcm)
b) √ 2. sin (x - π/4)
= √ 2. (sinx. cos π/4 - sin π/4. cosx)
= √ 2. (√ 2/2. sinx - √ 2/2. cosx)
= √ 2. √ 2/2. sinx - √ 2. √ 2/2. cosx
= sinx – cosx (đpcm).
Trả lời câu hỏi Toán 11 Đại số Bài 3 trang 36: Giải phương trình: √3 sin3x – cos3x = √2.
Bài giải: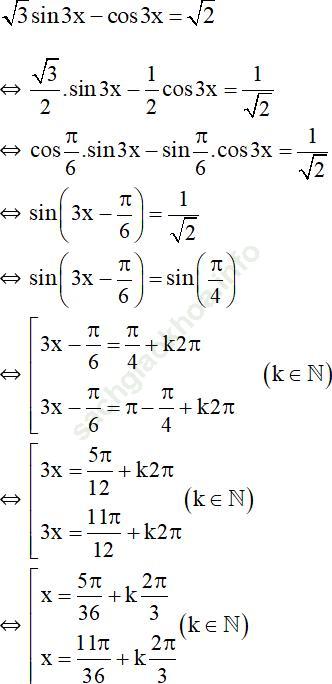
Giải bài 1 trang 36 sgk Đại số 11: Giải phương trình: sin2x – sin x = 0
Bài giải:
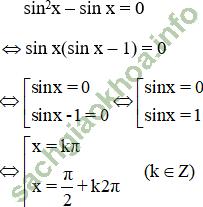
Vậy phương trình có tập nghiệm 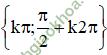
+ Phương trình sin x = sin α có họ nghiệm ![]() (k ∈ Z).
(k ∈ Z).
Đặc biệt:
sin x = 0
⇔ x = k. π (k ∈ Z).
sin x = 1
⇔ ![]() (k ∈ Z).
(k ∈ Z).
Giải bài 2 trang 36 sgk Đại số 11: Giải các phương trình sau:
a) 2cos2x – 3cos x + 1 = 0
b) 2sin 2x + √2. sin4x = 0.
Bài giải:
a. 2cos2x – 3cosx + 1 = 0 (1)
đặt t = cosx, điều kiện –1 ≤ t ≤ 1
(1) trở thành 2t2 – 3t + 1 = 0
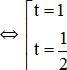 (thỏa mãn điều kiện).
(thỏa mãn điều kiện).
+ t = 1 ⇒ cos x = 1 ⇔ x = k. 2π (k ∈ Z)
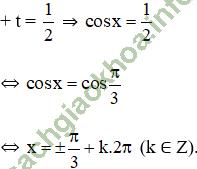
Vậy phương trình có tập nghiệm 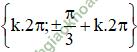

Vậy phương trình có tập nghiệm 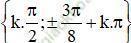 (k ∈ Z)
(k ∈ Z)
+ sin2a = 2. sina. cosa.
Giải bài 3 trang 37 sgk Đại số 11: Giải các phương trình sau:
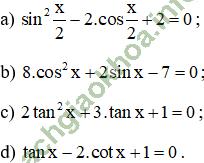
 ).
).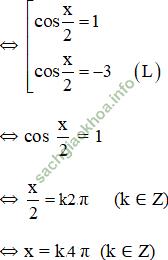
Vậy phương trình có họ nghiệm x = k4π (k ∈ Z)
b. 8cos2x + 2sinx – 7 = 0 (1)
⇔ 8 (1 – sin2x) + 2sinx – 7 = 0
⇔ 8sin2x - 2sinx – 1 = 0 (Phương trình bậc hai với ẩn sin x)
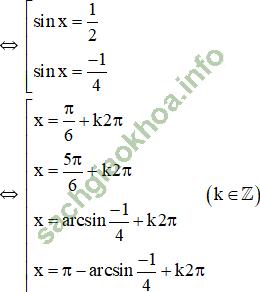
 + k2π;
+ k2π; 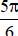 + k2π; arcsin
+ k2π; arcsin + k2π; π - arcsin
+ k2π; π - arcsin + k2π (k ∈ Z).
+ k2π (k ∈ Z).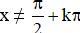
2tan2x + 3tanx + 1 = 0 (Phương trình bậc 2 với ẩn tan x).
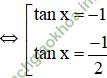

Vậy phương trình có tập nghiệm {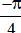 + kπ; arctan
+ kπ; arctan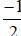 + kπ} (k ∈ Z)
+ kπ} (k ∈ Z)
d. Điều kiện 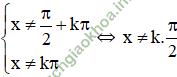
tanx – 2. cotx + 1 = 0
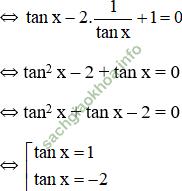

Vậy phương trình có tập nghiệm { + kπ; arctan (-2) + kπ} (k ∈ Z)
+ kπ; arctan (-2) + kπ} (k ∈ Z)
+ sin2α = 1 - cos2α với mọi α ∈ R.
+ ![]() với mọi α thỏa mãn điều kiện xác định.
với mọi α thỏa mãn điều kiện xác định.
Giải bài 4 trang 37 sgk Đại số 11: Giải các phương trình sau:
a. 2sin2 x + sinx. cosx – 3cos2 x = 0
b. 3sin2 x – 4 sinx. cosx + 5 cos2 x =2
c. sin2 x + sin2x - 2 cos2 x = 1/2
d. 2cos2x - 3√3sin2x - 4sin2x = -4
Bài giải:
a) 2sin2x + sinx. cosx – 3cos2x = 0 (1)
+ Xét cos x = 0 ⇒ sin2x = 1 – cos2x = 1
Phương trình (1) trở thành: 2 = 0 (loại)
+ Xét cos x ≠ 0, chia cả hai vế của (1) cho cos2x ta được:
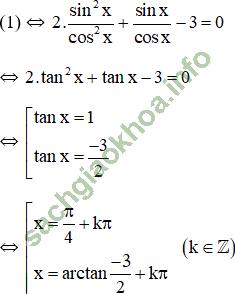
Vậy phương trình có tập nghiệm  (k ∈ Z)
(k ∈ Z)
b) 3sin2x – 4sinx. cosx + 5cos2x = 2
⇔ 3sin2x – 4sinx. cosx + 5cos2x = 2 (sin2x + cos2x)
⇔ sin2x – 4sinx. cosx + 3 cos2x = 0 (1)
+ Xét cosx = 0 ⇒ sin2x = 1.
Phương trình (1) trở thành 1 = 0 (Vô lý).
+ Xét cos x ≠ 0. Chia hai vế phương trình cho cos2x ta được:

Vậy phương trình có tập nghiệm 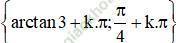 (k ∈ Z)
(k ∈ Z)
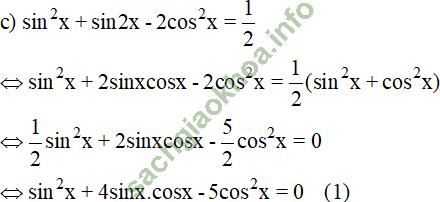
+ Xét cos x = 0 ⇒ sin2x = 1 – cos2x = 1
(1) trở thành 1 = 0 (Vô lý).
+ Xét cos x ≠ 0, chia cả hai vế cho cos2x ta được:
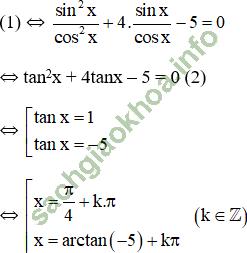
 (k ∈ Z)
(k ∈ Z)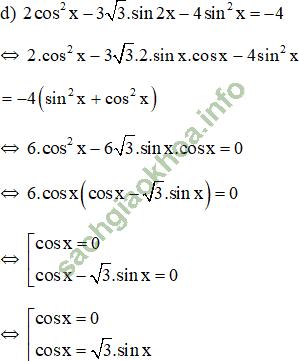
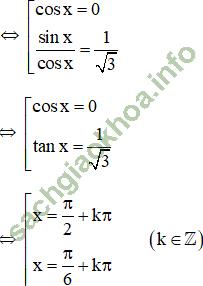
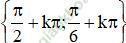 (k ∈ Z)
(k ∈ Z)Phương trình a. sin2x + b. sinx. cosx + c. cos2x = 0 được gọi là phương trình đẳng cấp bậc 2 đối với sin và cos.
Phương pháp giải:
+ Xét cos x = 0.
+ Xét cos x ≠ 0, chia cả hai vế của phương trình cho cos2x ta thu được phương trình bậc 2 với ẩn tan x rồi giải phương trình.
Giải bài 5 trang 37 sgk Đại số 11: Giải các phương trình sau:
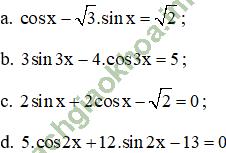
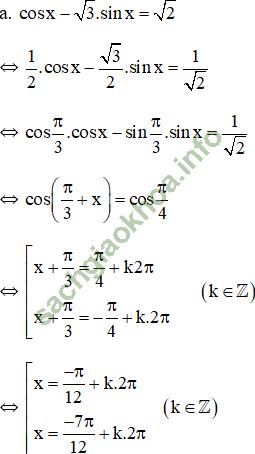
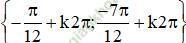 (k ∈ Z)
(k ∈ Z)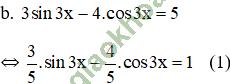
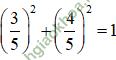 nên tồn tại α thỏa mãn
nên tồn tại α thỏa mãn 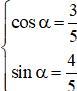

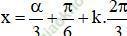 (k ∈ Z) với α thỏa mãn
(k ∈ Z) với α thỏa mãn 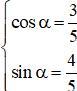
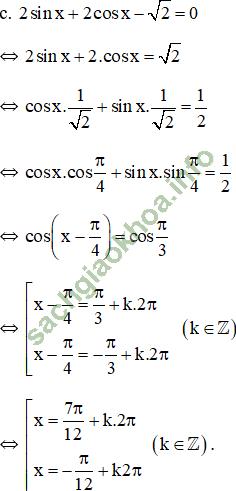
 (k ∈ Z)
(k ∈ Z)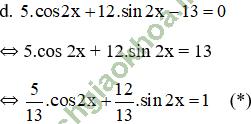


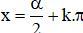 (k ∈ Z) với α thỏa mãn
(k ∈ Z) với α thỏa mãn 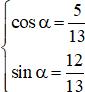 Kiến thức áp dụng:
Kiến thức áp dụng:+ Phương trình bậc nhất đối với sin và cos có dạng:
a. sin x + b. cos x = c (a ≠ 0; b ≠ 0)
+ Cách giải: Chia cả hai vế cho ![]() ta được:
ta được:
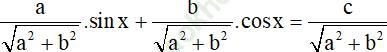
Vì 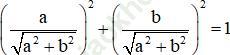 nên tồn tại α thỏa mãn
nên tồn tại α thỏa mãn 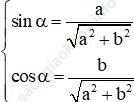
Khi đó phương trình trở thành:
+) sin (a ± b) = sina. sinb ± cos a. cos b
+) cos (a ± b) = cos a. cos b ∓ sin a. sin b.
Giải bài 6 trang 37 sgk Đại số 11: Giải các phương trình sau:
a. tan (2x + 1).tan (3x – 1) = 1
b. tanx + tan (x+π/4) = 1
Bài giải:
a. Điều kiện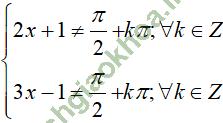

Vậy phương trình có họ nghiệm 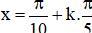 (k ∈ Z).
(k ∈ Z).
b. Điều kiện:

⇔ tan x. (1 - tanx) + tanx + 1 = 1 – tan x.
⇔ tan x - tan2x + 2. tan x = 0
⇔ tan2x - 3tanx = 0
⇔ tanx (tanx - 3) = 0
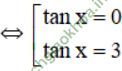
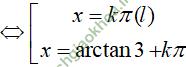
Vậy phương trình đã cho có tập nghiệm là: {arctan 3+kπ; k ∈ Z}
+) ![]()