Ôn tập chương 1 - Giải BT Toán 11
Bài tập (trang 40-41)
Bài tập trắc nghiệm (trang 41)
Giải bài 1 trang 40 sgk Đại số 11:
a. Hàm số y = cos3x có phải là hàm số chẵn không? Vì sao?
b. Hàm số y = tan (x+ π/5) có phải là hàm số lẻ không? Vì sao?
Bài giải:
a. y = f (x) = cos3x là hàm số chẵn vì:
+ TXĐ: D = R ⇒ ∀ x ∈ D ta có: - x ∈ D
+ f (-x) = cos3. (-x) = cos (-3x) = cos 3x = f (x) ∀ x ∈ D
b. Ta có:
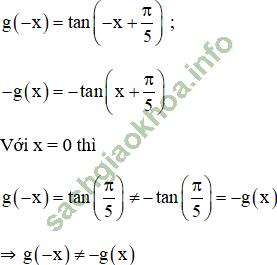
⇒ g (x) không phải hàm số lẻ.
+ Hàm f (x) được gọi là hàm số chẵn nếu thỏa mãn đồng thời hai điều kiện:
Với ∀ x ∈ D thì –x ∈ D.
f (-x) = f (x) với mọi x ∈ D.
+ Hàm g (x) được gọi là hàm số lẻ nếu thỏa mãn đồng thời hai điều kiện:
Với mọi x ∈ D thì –x ∈ D
g (-x) = -g (x) với mọi x ∈ D.
Bài 2 (trang 40 SGK Đại số 11): Căn cứ vào đồ thị hàm số y = sinx, tìm những giá trị của x trên đoạn [-3π /2; 2π] để hàm số đó:
a. Nhận giá trị bằng – 1
b. Nhận giá trị âm
Bài giải:Xét đồ thị hàm số y = sin x trên 
:
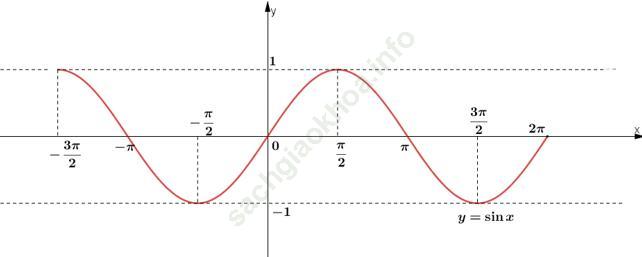
a. sin x = -1
⇔ 
(Hoành độ giao điểm của đồ thị hàm số và đường thẳng y = -1).
b. sin x < 0
⇔ x ∈ (-π; 0) ∪ (π; 2π) (Các khoảng mà đồ thị nằm phía dưới trục hoành).
Giải bài 3 trang 41 sgk Đại số 11: Tìm giá trị lớn nhất của các hàm số sau:
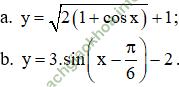
Ta có: với mọi x ∈ R: -1 ≤ cos x ≤ 1
⇒ 0 ≤ 1 + cos x ≤ 2
⇒ 0 ≤ 2 (1 + cos x) ≤ 4
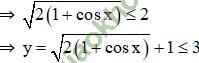
y = 3 ⇔ cos x = 1 ⇔ x = k. 2π (k ∈ Z).
Vậy giá trị lớn nhất của hàm số đạt được là 3 khi x = k. 2π (k ∈ Z).
Vậy giá trị lớn nhất của hàm số đạt được là 1 khi 
(k ∈ Z).
+ Với mọi x ∈ R ta luôn có: -1 ≤ sin x ≤ 1; -1 ≤ cos x ≤ 1.
Giải bài 4 trang 41 sgk Đại số 11: Giải phương trình sau:
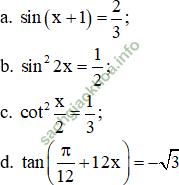
Vậy phương trình có tập nghiệm: {arcsin
– 1 + k2π; π - arcsin – 1 + k2π} (k ∈ Z)
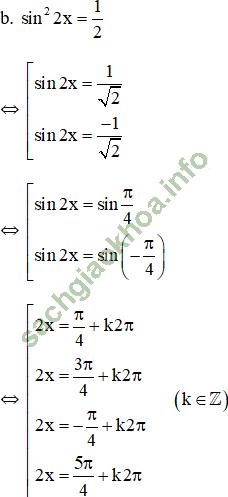
Vậy phương trình có họ nghiệm 
(k ∈ Z)
* Lưu ý: Về cách gộp, tách, loại họ nghiệm xem lại phần kiến thức áp dụng bài 5 trang 29. Không nhất thiết phải gộp các họ nghiệm lại.
c. Điều kiện: 
(k ∈ Z).
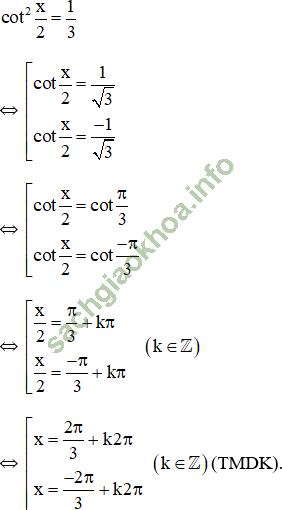
Vậy phương trình có tập nghiệm 
d. Điều kiện:
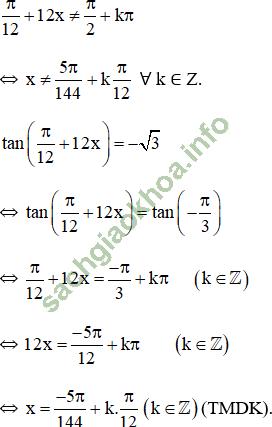
Vậy phương trình có tập nghiệm 
+ Phương trình sin x = sin α có nghiệm 
+ Phương trình cos x = cos α có nghiệm x = ±α + k. 2π (k ∈ Z).
+ Phương trình tan x = tan α có nghiệm x = α + k. π, (k ∈ Z)
+ Phương trình cot x = cot α có nghiệm x = α + k. π, (k ∈ Z).
+ Với các phương trình chứa tan và cot phải có điều kiện xác định.
Giải bài 5 trang 41 sgk Đại số 11: Giải các phương trình sau:
a. 2cos2x – 3cosx + 1 = 0
b. 25sin2x + 15sin2x + 9cos2x = 25
c. 2sinx + cosx = 1
d. sinx + 1,5cotx = 0
Bài giải:
a. 2cos2x – 3cosx + 1 = 0 (Phương trình bậc hai với ẩn cos x).
Vậy phương trình có tập nghiệm 
b. 25sin2x + 15sin2x + 9cos2x = 25
⇔ 25sin2x + 15.2sinx. cosx + 9cos2x – 25 = 0
⇔ 25. (sin2x – 1) + 15.2. sinx. cosx + 9cos2x = 0
⇔ -25. cos2x + 30sinx. cosx + 9cos2x = 0
⇔ 16. cos2x – 30. sinx. cosx = 0
⇔ 2. cosx. (8cosx – 15sinx) = 0
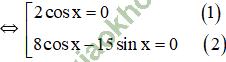
+ Giải (1): 2. cos x = 0 ⇔ cos x = 0
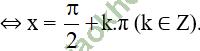
+ Giải (2): 8. cos x – 15. sin x = 0
⇔ 8. cos x = 15. sin x.
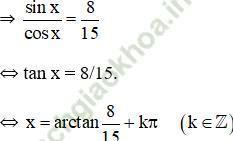
Vậy phương trình có tập nghiệm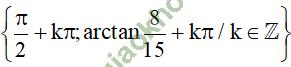 
c. 2. sin x + cos x = 1
nên tồn tại α thỏa mãn 
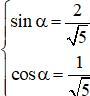
(1) trở thành:
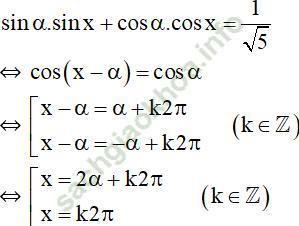
Vậy phương trình có nghiệm {k2π; 2α+k2π/k ∈ Z}
với α thỏa mãn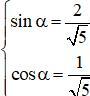 
Phương trình trên là phương trình bậc nhất đối với sin và cos.
Phương pháp giải: Xem lại kiến thức áp dụng bài 5 trang 37.
d. Điều kiện x ≠ kπ ∀ k ∈ Z
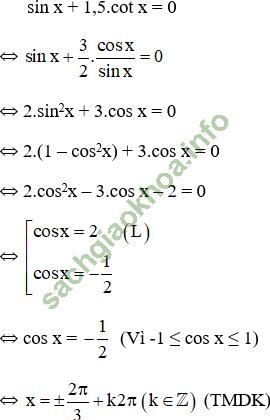
+ Phương trình sin x = sin α có nghiệm
+ Phương trình cos x = cos α có nghiệm x = ±α + k. 2π (k ∈ Z).
+ Phương trình tan x = tan α có nghiệm x = α + k. π, (k ∈ Z)
+ Phương trình cot x = cot α có nghiệm x = α + k. π, (k ∈ Z).
+ sin 2x = 2. sin x. cos x
Phần bài tập trắc nghiệm:
Bài 6 (trang 41 SGK Đại số 11): Phương trình cos x = sin x có số nghiệm thuộc đoạn [-π; π] là:
A. 2
B. 4
C. 5
D. 6
Trả lờiĐáp án đúng là: A.
Giải thích:
sin x = cos x
⇒ tan x = 1
Vậy phương trình có hai nghiệm thuộc [-π; π]
Giải bài 7 trang 41 sgk Đại số 11:
Trả lời:
Đáp án đúng là: A
Giải thích:
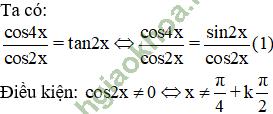
(1) ⇔ cos4x = sin 2x
⇔ 1 – 2sin22x = sin2x
Suy ra, phương trình đã cho có 2 nghiệm thuộc khoảng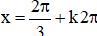 
cos2a = 2cos2a – 1 = 1 – 2sin2a = cos2a – sin2a.
Bài 8 (trang 41 SGK Đại số 11): Nghiệm dương nhỏ nhất của phương trình sin x + sin 2x = cos x + 2 cos2x là:
Trả lời:
Đáp án đúng là: C.
Giải thích:
Cách 1:
sin x + sin2x = cosx + 2cos2x
⇔ sin x + 2sinx. cosx = cosx (1 + 2cosx)
⇔ sinx (1 + 2cosx) = cosx. (1 + 2cosx)
⇔ (sin x – cos x)(1 + 2. cos x) = 0
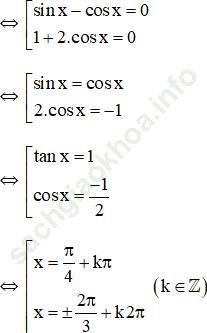
Cách 2: Thử các đáp án nhận thấy chỉ có 
và 
là nghiệm của phương trình.
nên chọn
Bài 9 (trang 41 SGK Đại số 11): Nghiệm âm lớn nhất của phương trình 2tan2x + 5 tanx + 3 = 0 là:
Trả lời:
Đáp án đúng là: B.
Giải thích:
Ta có: 2tan2x + 5 tan x + 3 = 0
Bài 10 (trang 41 SGK Đại số 11): Phương trình 2tanx – 2cotx – 3 = 0 có số nghiệm thuộc khoảng (-π /2; π) là:
A. 1
B. 2
C. 3
D. 4
Trả lời:Đáp án đúng là: C.
Giải thích.
2tanx – 2cotx – 3 = 0 (1)
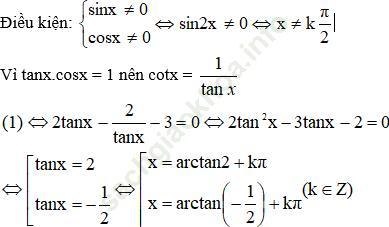
Có ba nghiệm thuộc 
là {arctan2; arctan 
; arctan 
+ π}