Ôn tập chương 2 - Giải BT Toán 11

Ôn tập chương 2

Bài 1 (trang 76 SGK Đại số 11): Phát biểu quy tắc cộng

Bài giải:

Quy tắc cộng:

Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động thứ nhất có m cách thực hiện, hành động thứ hai có n cách thực hiện không trùng với bất kì cách nào của hành động thứ nhất thì công việc đó có m + n cách thực hiện.

Quy tắc cộng có thể mở rộng với nhiều hành động.

+ Ví dụ:

Có hai tổ học sinh tham gia lao động, tổ thứ nhất có 8 học sinh, tổ thứ hai có 10 học sinh. Hỏi cô giáo có bao nhiêu cách chọn ra 3 học sinh thuộc cùng một tổ?

Giải:

TH1: Chọn 3 học sinh thuộc tổ thứ nhất:

⇒ Có: C³₈ = 56 cách chọn.

TH2: Chọn 3 học sinh thuộc tổ thứ hai:

⇒ Có: C³₁₀ = 120 cách chọn.

Theo quy tắc cộng ⇒ Cô giáo có: 120 + 56 = 176 (cách chọn).

Bài 2 (trang 76 SGK Đại số 11): Phát biểu quy tắc nhân

Bài giải:

+ Quy tắc nhân:

Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu hành động thứ nhất có m cách thực hiện, hành động thứ hai có n cách thực hiện thì công việc đó được hoàn thành bởi m. n cách thực hiện.

Quy tắc nhân có thể mở rộng đối với nhiều hành động liên tiếp.

+ Ví dụ áp dụng:

Một nhóm học sinh gồm 8 nam và 10 nữ tham gia văn nghệ. Cô giáo cần chọn ra một đội gồm 2 nam và 2 nữ để biểu diễn một tiết mục múa. Hỏi cô giáo có bao nhiêu cách chọn?

Giải:

Việc chọn 2 nam và 2 nữ là một công việc cần hoàn thành bởi 2 bước liên tiếp:

+ Chọn 2 học sinh nam: Có C²₈ = 28 (cách chọn).

+ Chọn 2 học sinh nữ: Có C²₁₀ = 45 (cách chọn)

⇒ Theo quy tắc nhân: Có 28.45 = 1260 (cách chọn).

Bài 3 (trang 76 SGK Đại số 11): Phân biệt sự khác nhau giữa một chỉnh hợp chập k của n phần tử và một tổ hợp chập k của n phần tử.

Bài giải:

- Chỉnh hợp chập k của n phần tử là một tập hợp con k phần tử của một tập hợp n phần tử được sắp xếp theo một thứ tự nào đó.

- Tổ hợp chập k của n phần tử là tập hợp con k phần tử của một tập hợp n phần tử không để ý đến thứ tự các phần tử của tập hợp con đó.

Bài 4 (trang 76 SGK Đại số 11): Có bao nhiêu số chẵn có bốn số được tạo thành từ các chữ số 0,1,2,3,4,5,6 sao cho:

a) Các chữ số có thể giống nhau

b) Các chữ số khác nhau

Bài giải:

a. Có 4 cách chọn chữ số hàng đơn vị

6 cách chọn chữ số hàng nghìn

7 cách chọn chữ số hàng trăm

7 cách chọn chữ số hàng chục

⇒ Theo quy tắc nhân: Có 4.6.7.7 = 1176 (số)

b. TH1: Chọn các số chẵn có chữ số hàng đơn vị bằng 0

⇒ Có 6 cách chọn chữ số hàng nghìn

5 cách chọn chữ số hàng trăm

4 cách chọn chữ số hàng chục

⇒ Theo quy tắc nhân: có 6.5.4 = 120 (số)

TH2: Chọn các số chẵn có chữ số hàng đơn vị khác 0.

⇒ Có 3 cách chọn chữ số hàng đơn vị

Có 5 cách chọn chữ số hàng nghìn (khác 0 và khác hàng đơn vị)

Có 5 cách chọn chữ số hàng trăm

Có 4 cách chọn chữ số hàng chục

⇒ Theo quy tắc nhân: Có 3.5.5.4 = 300 (số)

⇒ Theo quy tắc cộng: Có tất cả 120 + 300 = 420 số chẵn thỏa mãn.

Bài 5 (trang 76 SGK Đại số 11): Xếp ngẫu nhiên ba bạn nam và ba bạn nữ ngồi thành sáu ghế kê theo hàng ngang. Tìm xác suất cho:

a. Nam, nữ ngồi xen kẽ nhau.

b. Ba bạn nam ngồi bên cạnh nhau.

Bài giải:

Không gian mẫu là việc sắp xếp 6 bạn vào 6 ghế tùy ý

⇒ n (Ω) = P₆ = 6! = 720.

a. Gọi A: “ Nam, nữ ngồi xen kẽ nhau”

+ Chọn chỗ ngồi cho 3 bạn nữ: Có 2 cách (Vị trí 1,3,5 hoặc 2,4,6).

+ Sắp xếp 3 bạn nữ vào 3 chỗ: Có 3! = 6 cách

+ Sắp xếp 3 bạn nam vào 3 chỗ còn lại: Có 3! = 6 cách

⇒ Theo quy tắc nhân: n (A) = 2.6.6 = 72 (cách).

⇒ n (A) = 2.3!. 3! = 72

b. B: “Ban bạn nam ngồi cạnh nhau”

+ Chọn 3 chỗ ngồi cạnh nhau cho 3 bạn nam: Có 4 cách.

+ Sắp xếp 3 bạn nam vào 3 chỗ: Có 3! = 6 cách.

+ Sắp xếp 3 bạn nữ vào 3 chỗ còn lại: Có 3! = 6 cách

⇒ Theo quy tắc nhân: n (B) = 4.6.6 = 144 (cách)

Xác suất để ba bạn nam ngồi cạnh nhau là:

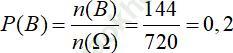
Bài 6 (trang 76 SGK Đại số 11): Từ một hộp chứa sáu quả cầu trắng và bốn quả cầu đen, lấy ngẫu nhiên đồng thời bốn quả, tính xác suất sao cho:

a. Bốn quả lấy ra cùng màu;

b. Có ít nhất một quả màu trắng.

Bài giải:

Không gian mẫu là kết quả việc chọn ngẫu nhiên 4 quả cầu từ hộp 10 quả cầu.

a. A: “ Bốn quả lấy ra cùng màu”

TH1: Bốn quả lấy ra cùng đen

TH2: Bốn quả lấy ra cùng trắng

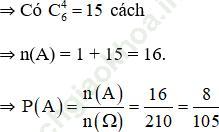
b. B: “ Cả 4 quả lấy ra đều màu đen”

⇒ B−: “ Có ít nhất 1 quả màu trắng”.

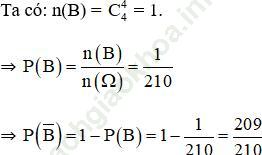
Bài 7 (trang 77 SGK Đại số 11): Gieo một con súc sắc ba lần. Tính xác suất sao cho mặt sáu chấm xuất hiện ít nhất một lần

Bài giải:

Không gian mẫu là kết quả của việc gieo 3 lần súc sắc

⇒ n (Ω) = 6.6.6 = 216.

A: “ Mặt 6 chấm xuất hiện ít nhất 1 lần”

⇒ A−: “ Không xuất hiện mặt 6 chấm”

Bài 8 (trang 77 SGK Đại số 11): Cho một lục giác đều ABCDEF. Viết các chữ cái A, B, C, D, E, F vào sáu cái thẻ. Lấy ngẫu nhiên hai thẻ. Tìm xác suất sao cho đoạn thẳng mà các đầu mút là các điểm được ghi trên hai thẻ đó là:

a. Cạnh của lục giác.

b. Đường chéo của lục giác.

c. Đường chéo nối hai đỉnh đối diện của lục giác.

Bài giải:

Không gian mẫu là kết quả của việc chọn ngẫu nhiên 2 thẻ trong số 6 thẻ.

a. Gọi A: “ Hai điểm là đầu mút của cạnh của lục giác”

⇒ n (A) = 6 (Lục giác có 6 cạnh)

b. Gọi B: “ Hai điểm là đầu mút của đường chéo”

⇒ B = A− (Vì một đoạn thẳng chỉ có thể là một cạnh hoặc một đường chéo)

⇒ P (B) = 1 – P (A) = 1 – 0,4 = 0,6

c. Gọi C: “ Hai điểm là đầu mút của đường chéo nối hai đỉnh đối diện”

⇒ n (C) = 3

Bài 9 (trang 77 SGK Đại số 11): Gieo đồng thời hai con súc sắc. Tính xác suất sao cho:

a. Hai con súc sắc đều xuất hiện mặt chẵn.

b. Tích các số chấm trên hai con súc sắc là số lẻ.

Bài giải:

Không gian mẫu là kết quả của việc gieo đồng thời hai con xúc sắc.

⇒ Ω = {(i; j); 1 ≤ i, j ≤ 6}.

⇒ n (Ω) = 6.6 = 36.

a) Gọi A: “Cả hai con xúc sắc đều xuất hiện mặt chẵn”

⇒ A = {(2; 2); (2; 4); (2; 6); (4; 2); (4; 4); (4; 6); (6; 2); (6; 4); (6; 6)}

⇒ n (A) = 9.

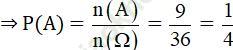
b) Gọi B: “Tích số chấm trên hai con xúc sắc là số lẻ”

Vì tích hai số là lẻ chỉ khi cả hai thừa số đều lẻ nên:

B = {(1; 1); (1; 3); (1; 5); (3; 1); (3; 3); (3; 5); (5; 1); (5; 3); (5; 5)}

⇒ n (B) = 9

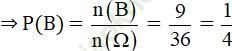
Bài 10 (trang 77 SGK Đại số 11): Lấy hai con bài từ cỗ bài tú lơ khơ 52 con. Số cách lấy là:

A. 104

B. 1326

C. 450

D. 2652

Bài giải:

Chọn đáp án B.

Giải thích:

Việc chọn 2 con bài từ cỗ bài 52 con là việc lấy ra tập hợp 2 phần tử từ tập hợp 52 phần tử và là tổ hợp chập 2 của 52

⇒ Có:

cách chọn.

Bài 11 (trang 77 SGK Đại số 11): Năm người được xếp vào ngồi quanh một bàn tròn với năm ghế. Số cách xếp là:

A. 50

B. 100

C. 120

D. 24

Bài giải:

Chọn đáp án D

Giải thích:

Với 5 người A, B, C, D, E xếp hàng ngang (hay dọc) thì có 5! = 120 cách xếp. Nhưng với 5 hoán vị khác nhau theo hàng ngang là ABCDE, DEABC, CDEAB nhưng xếp quanh bàn tròn như hình vẽ chỉ là một cách xếp. Vậy số cách xếp 5 người ngồi quanh bàn tròn là:

n = 5! /5= 4! = 24 (cách)

Bài 12 (trang 77 SGK Đại số 11): Gieo một con súc sắc hai lần. Xác suất để ít nhất một lần xuất hiện mặt sáu chấm.

Bài giải:

Chọn đáp án B.

Giải thích:

Không gian mẫu có: 6 × 6 = 36 phần tử.

Số trường hợp gieo hai con súc sắc không có con nào 6 chấm là: 5 × 5 = 25.

Số trường hợp hai con súc sắc có ít nhất một con 6 là: 36 – 25 = 11.

Xác suất để ít nhất một con súc sắc xuất hiện 6 chấm là:

P (A) = 11/36

Chọn đáp án B.

Bài 13 (trang 77 SGK Đại số 11): Từ một hộp chứa 3 quả cầu trắng và hai quả cầu đen lấy ngẫu nhiên hai quả. Xác suất để lấy được cả hai quả trắng là:

Bài giải:

Số cách lấy 2 quả cầu bất kì là:

Số cách lấy được 2 quả cầu trắng là:

Xác suất để lấy được hai quả cầu trắng là:

Chọn đáp án A.

Bài 14 (trang 77 SGK Đại số 11): Gieo ba con súc sắc. Xác suất để số chấm xuất hiện trên ba con như nhau là:

Bài giải:

Không gian mẫu có 6³ = 216 phần tử.

Số trường hợp cả ba con súc sắc xuất hiện cùng số chấm là 6 trường hợp.

Xác suất cần tìm là: 6/216

Chọn đáp án C.

Bài 15 (trang 78 SGK Đại số 11): Gieo một đồng tiền cân đối và đồng chất bốn lần. Xác suất để cả bốn lần xuất hiện mặt sấp là:

Bài giải:

Số trường hợp xảy ra có thể là: 2⁴ = 16

Chỉ có duy nhất một trường hợp cả 4 lần đều xuất hiện sấp.

Xác suất cần tính là: P (X) = 1/16

Chọn đáp án C.

Bài trước: Bài 5: Xác suất của biến cố - Giải BT Toán 11 Bài tiếp: Bài 1: Phương pháp quy nạp toán học - Giải BT Toán 11