Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau - Giải BT Toán 11
Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau
Trả lời câu hỏi Toán 11 Hình học Bài 6 trang 20: Cho hình vuông ABCD, gọi O là giao điểm của AC và BD. Tìm ảnh của các điểm A, B, O qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc 90° và phép đối xứng qua đường BD (h. 1.41).
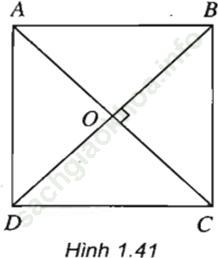
Bài giải:
- Ảnh của A, B, O qua phép quay tâm O góc 90o lần lượt là: D, A, O
- Ảnh của D, A, O qua phép đối xứng qua đường thẳng BD là: D, C, O
Trả lời câu hỏi Toán 11 Hình học Bài 6 trang 21: Hãy chứng minh tính chất 1.
Gợi ý. Sử dụng tính chất điểm B nằm giữa hai điểm A và C khi và chỉ khi AB + BC = AC (h. 1.43).
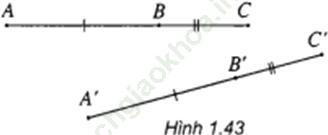
Bài giải:
Áp dụng định nghĩa: phép dời hình là phép biến hình bảo toàn khoảng cảnh giữa hai điểm bất kỳ
Nên ảnh của 3 điểm A, B, C qua phép dời hình F là 3 điểm A', B', C'
Khi đó:
AB = A'B', BC = B'C', AC = A'C'
Ta có: A, B, C thằng hàng và B nằm giữa A và C ⇒ AB + BC = AC
⇒ A'B' + B'C' = A'C'
Hay A', B', C' thẳng hàng và B' nằm giữa A' và C'
Trả lời câu hỏi Toán 11 Hình học Bài 6 trang 21: Gọi A’, B’ lần lượt là ảnh của A, B qua phép dời hình F. Chứng minh rằng nếu M là trung điểm của AB thì M’ = F (M) là trung điểm của A’B’.
Bài giải:
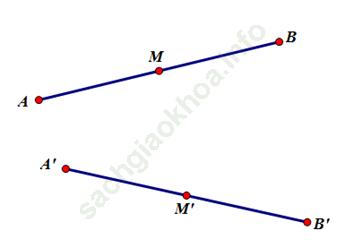
Gọi A', B', M' lần lượt là ảnh của A, B, M qua phép dời hình F
Theo tính chất 1 ⇒ AB = A'B' và AM = A'M' (1)
M là trung điểm AB ⇒ AM = 1/2 AB
Kết hợp (1) ⇒ A'M' = 1/2 A'B' ⇒ M' là trung điểm A'B'
Trả lời câu hỏi Toán 11 Hình học Bài 6 trang 22: Cho hình chữ nhật ABCD. Gọi E, F, H, I theo thứ tự là trung điểm của các cạnh AB, CD, BC, EF. Hãy tìm một phép dời hình biến tam giác AEI thành tam giác FCH (h. 1.46)
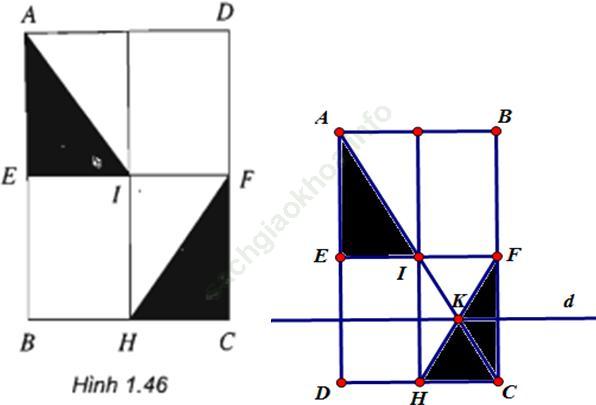
Bài giải:
- Phép đối xứng qua tâm I biến Δ AEI thành Δ CFI
- Phép đối xứng qua trục d biến Δ CFI thành Δ FCH
Trả lời câu hỏi Toán 11 Hình học Bài 6 trang 23: Cho hình chữ nhật ABCD. Gọi I là giao điểm của AC và BD. Gọi E, F theo thứ tự là trung điểm của AD và BC. Chứng minh rằng các hình thang AEIB và CFID bằng nhau.
Bài giải: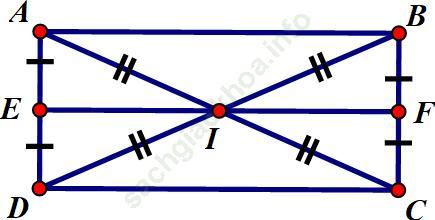
I là giao điểm AC và BD nên I là trung điểm của AC và BD
Mà AC = BD ⇒ AI = BI = 1/2 AC = 1/2 BD
Gọi E, F theo thứ tự là trung điểm của AD và BC ⇒ EF là đường trung bình của hình chữ nhật ABCD và AE = BF = 1/2 AD = 1/2 BC
⇒ EF // AB ⇒ EF vuông góc với AD và EF vuông góc với BC
Xét hai tam giác vuông AEI và BFI có:
AI = BI
AE = BF
⇒ Δ AEI = Δ BFI (cạnh huyền – cạnh góc vuông)
⇒ EI = FI (hai cạnh tương ứng)
⇒ I là trung điểm EF
Do đó, phép đối xứng qua tâm I biến hình thang AEIB thành hình thang CFID
⇒ Hai hình thang AEIB và CFID bằng nhau
Giải bài 1 trang 23 sgk Hình học 11:
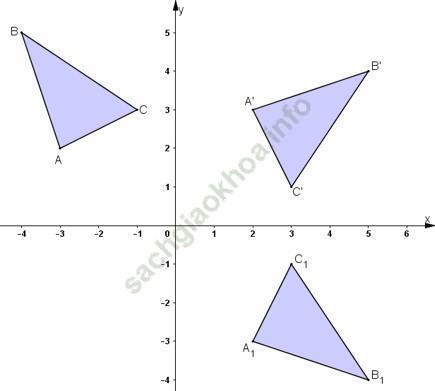
Trong mặt phẳng Oxy cho các điểm A (-3; 2), B (-4; 5) và C (-1; 3).
a. Chứng minh rằng các điểm A’ (2; 3), B’ (5; 4) và C’ (3; 1) theo thứ tự là ảnh của A, B và C qua phép quay tâm O góc –90o.
b. Gọi tam giác A1B1C1 là ảnh của tam giác ABC qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc –90o và phép đối xứng qua trục Ox. Tìm tọa độ các đỉnh của tam giác A1B1C1.
Bài giải:
a) + Ta có:

+ Chứng minh hoàn toàn tương tự ta được
![]()
b. ΔA1B1C1 là ảnh của ΔABC qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc –90º và phép đối xứng qua trục Ox.
⇒ ΔA1B1C1 là ảnh của ΔA’B’C’ qua phép đối xứng trục Ox.
⇒ A1 = ĐOx(A’) ⇒ A1(2; -3)
B1 = ĐOx(B’) ⇒ B1(5; -4)
C1 = ĐOx(C’) ⇒ C1(3; -1).
Kiến thức áp dụng: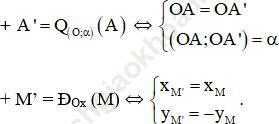
Giải bài 2 trang 24 sgk Hình học 11: Cho hình chữ nhật ABCD. Gọi E, E, H, K, O, I, J lần lượt là trung điểm của các cạnh AB, BC, CD, DA, KF, HC, KO. Chứng minh hai hình thang AEJK và FOIC bằng nhau.
Bài giải:
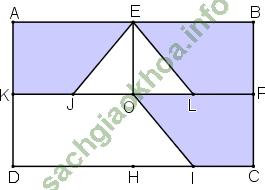
Gọi L là trung điểm của OF.
+ Vì EO là đường trung trực của các đoạn thẳng AB; KF; JL
⇒ B = ĐEO (A); F = ĐEO (K); L = ĐEO (J); E = ĐEO (E)
⇒ Hình thang BFLE là ảnh của hình thang AKJE qua phép đối xứng trục EO.
⇒ Hai hình thang BFLE và AKJE bằng nhau (1)
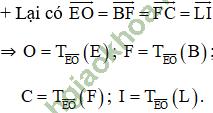
⇒ Hình thang FCIO là ảnh của hình thang BFLE qua phép tịnh tiến theo 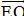
⇒ Hai hình thang FCIO và BFLE bằng nhau (2)
Từ (1) và (2) ⇒ hai hình thang FCIO và AKJE bằng nhau.
Kiến thức áp dụng:+ A’ = Đd (A) ⇔ d là đường trung trực của AA’.
+ ![]()
+ Các phép tịnh tiến, đối xứng trục, đối xứng tâm, phép quay được gọi là các phép dời hình.
+ Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
Giải bài 3 trang 24 sgk Hình học 11: Chứng minh rằng: Nếu một phép dời hình biến tam giác ABC thành tam giác A’B’C’ thì nó cũng biến trọng tâm của tam giác ABC tương ứng thành trọng tâm của tam giác A’B’C’.
Bài giải:
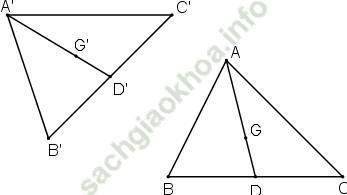
Gọi f là phép dời hình biến tam giác ABC thành tam giác A’B’C’.
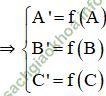
Gọi D là trung điểm của BC, D’ = f (D).
Gọi G là trọng tâm ΔABC, G’ = f (G).
+ B, D, C thẳng hàng ⇒ B’; D’; C’ thẳng hàng.
+ A; G; D thẳng hàng ⇒ A’; G’; D’ thẳng hàng.
+ B’D’ = BD = BC/2 = B’C’/2 ⇒ D’ là trung điểm B’C’.
+ A’G’ = AG = 2. AD/3 = 2. A’D’/3 ⇒ G’ là trọng tâm ΔA’B’C’.
Vậy phép dời hình f biến trọng tâm G của ΔABC thành trọng tâm G’ của ΔA’B’C’ (đpcm).
Kiến thức áp dụng:+ Phép dời hình biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm.
+ Phép dời hình biến đoạn thẳng thành đoạn thẳng bằng nó.