Bài 2: Dãy số - Giải BT Toán 11
Bài 2: Dãy số
Trả lời câu hỏi Toán 11 Đại số Bài 2 trang 85: Cho hàm số f (n) = 1/ (2n-1), n ∈ N*. Tính f (1), f (2), f (3), f (4), f (5).
Bài giải: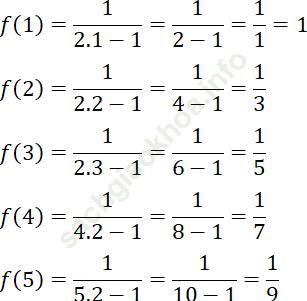
Trả lời câu hỏi Toán 11 Đại số Bài 2 trang 86: Hãy nêu các phương pháp cho một hàm số và ví dụ minh họa
Bài giải:
- Hàm số cho bằng bảng
Ví dụ:
| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 3 | 5 | 7 | 9 |
- Hàm số cho bằng công thức:
Ví dụ:
Trả lời câu hỏi Toán 11 Đại số Bài 2 trang 86: Viết năm số hạng đầu và số hạng tổng quát của các dãy số sau:
a) Dãy nghịch đảo của các số tự nhiên lẻ;
b) Dãy các số tự nhiên chia cho 3 dư 1.
Bài giải:
a)năm số hạng đầu:
số hạng tổng quát của dãy số: 1/ (2n + 1)(n ∈ N)
b)năm số hạng đầu: 1; 4; 7; 10; 13
số hạng tổng quát của dãy số: 3n + 1 (n ∈ N)
Trả lời câu hỏi Toán 11 Đại số Bài 2 trang 87: Viết mười số hạng đầu của dãy Phi-bô-na-xi.
Bài giải:Mười số hạng đầu của dãy Phi-bô-na-xi: 1; 1; 2; 3; 5; 8; 13; 21; 34; 55
Trả lời câu hỏi Toán 11 Đại số Bài 2 trang 89: Cho các dãy số (un) và (vn) với un = 1 + 1/n; vn = 5n – 1.
a) Tính u(n+1), v(n+1).
b) Chứng minh u(n+1) < un và v(n+1) > vn, với mọi n ∈ N^*.
Bài giải:a) u(n+1) = 1 + 1/ (n+1); v(n+1) = 5 (n + 1) - 1 = 5n + 4
b) Ta có:
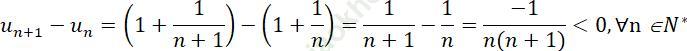
⇒ u(n+1) < un, ∀ n ∈ N*
v(n+1) - vn = (5n + 4) - (5n - 1) = 5 > 0
⇒ v(n+1) > vn, ∀ n ∈ N*
Trả lời câu hỏi Toán 11 Đại số Bài 2 trang 90: Chứng minh các bất đẳng thức
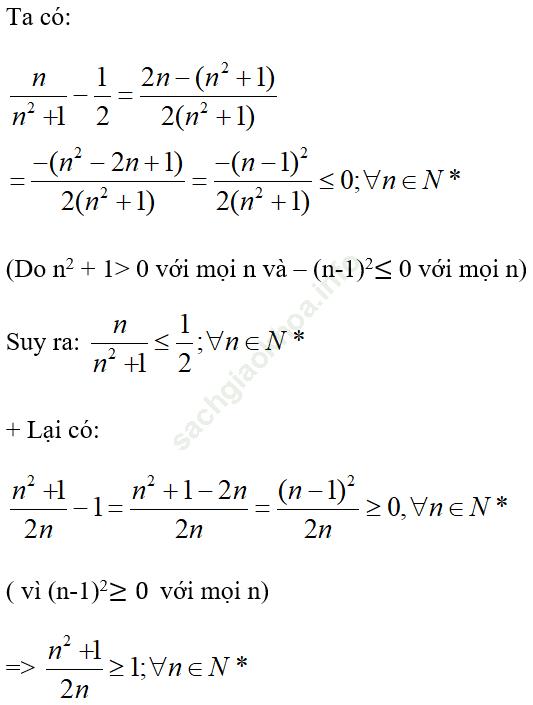
Bài 1 (trang 92 SGK Đại số 11): Viết năm số hạng đầu của dãy số có số hạng tổng quát un cho bởi công thức:
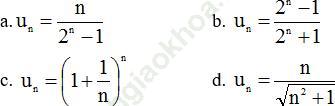
Bài giải:
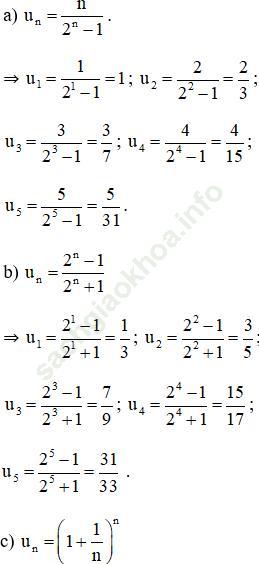
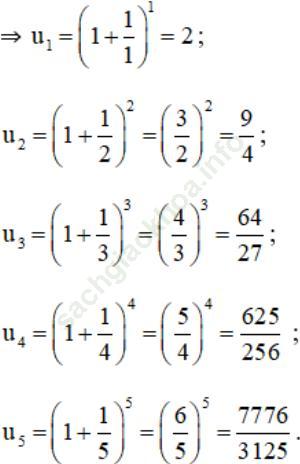
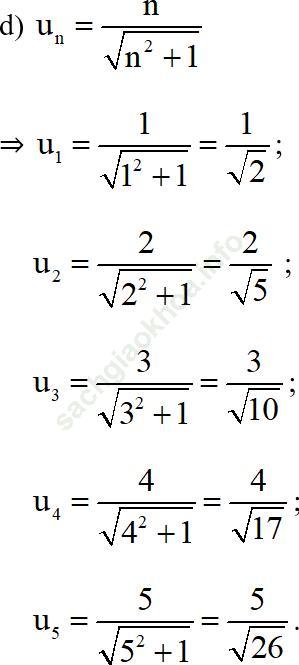
Bài 2 (trang 92 SGK Đại số 11): Cho dãy số (un), biết u1 = - 1, un+ 1 = un + 3 với n ≥ 1.
a. Viết năm số hạng đầu của dãy số;
b. Chứng minh bằng phương pháp quy nạp: un = 3n – 4
Bài giải:a. u1 = - 1, un + 1 = un + 3 với n > 1
u1 = - 1;
u2 = u1 + 3 = -1 + 3 = 2
u3 = u2 + 3 = 2 + 3 = 5
u4 = u3 + 3 = 5 + 3 = 8
u5 = u4 + 3 = 8 + 3 = 11
b. Chứng minh phương pháp quy nạp: un = 3n – 4 (1)
+ Khi n = 1 thì u1 = 3.1 - 4 = -1, vậy (1) đúng với n = 1.
+ Giả sử công thức (1) đúng với n = k > 1 tức là uk = 3k – 4.
+ Ta chứng minh (1) đúng với n= k+ 1 tức là chứng minh: uk+1 = 3 (k+1) - 4
Thật vậy, ta có: uk + 1 = uk + 3 = 3k – 4 + 3 = 3 (k + 1) – 4.
⇒ (1) đúng với n = k + 1
Vậy (1) đúng với ∀ n ∈ N*.
Bài 3 (trang 92 SGK Đại số 11): Dãy số (un) cho bởi u1 = 3, un+1 = √ (1+un2), n > 1
a. Viết năm số hạng đầu của dãy số.
b. Dự đoán công thức số hạng tổng quát un và chứng minh công thức đó bằng phương pháp quy nạp.
Bài giải:a. Năm số hạng đầu của dãy số
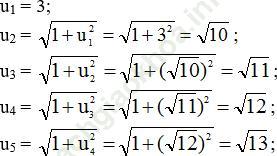
b. Dự đoán công thức số hạng tổng quát của dãy số:
un =√ (n+8) (1)
Rõ ràng (1) đúng với n = 1
Giả sử (1) đúng với n = k, nghĩa là uk = √ (k+8)
⇒ (1) đúng với n = k + 1
⇒ (1) đúng với mọi n ∈ N*.
Giải bài 4 trang 92 sgk Đại số 11: Xét tính tăng, giảm của các dãy số (un), biết:
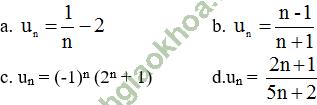
Bài giải:
a. Với mọi n ∈ N ta có:
![]()
⇒ (un) là dãy số giảm.
![]()
Với mọi n ∈ N có:
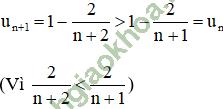
⇒ (un) là dãy số tăng.
c. un = (-1)n. (2n + 1)
Nhận xét: u1 < 0, u2 > 0, u3 < 0, u4 > 0, …
⇒ u1 < u2, u2 > u3, u3 < u4, …
⇒ dãy số (un) không tăng, không giảm.
![]()
Xét:
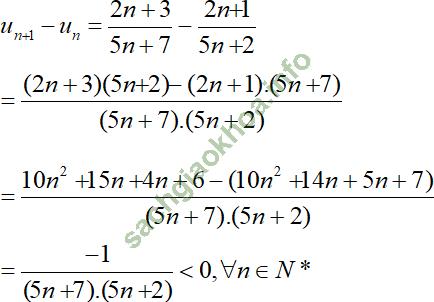
⇒ un + 1 – un < 0 ⇒ un + 1 < un
Vậy (un) là dãy số giảm
Kiến thức áp dụng:Dãy (un) được gọi là dãy số tăng nếu un + 1 > un với mọi n ∈ N*.
Dãy (un) được gọi là dãy số giảm nếu un + 1 < un với mọi n ∈ N*.
Giải bài 5 trang 92 sgk Đại số 11: Trong các dãy số (un) sau, dãy nào bị chặn dưới, bị chặn trên và bị chặn?

Bài giải:
a. un = 2n2 – 1
+ Với n ∈ N* ta có: n ≥ 1 và n2 ≥ 1
⇒ un = 2n2 – 1 ≥ 2.12 – 1 = 1.
⇒ un ≥ 1
⇒ dãy (un) bị chặn dưới ∀n ∈ N*.
+ (un) không bị chặn trên vì không có số M nào thỏa mãn:
un = 2n2 – 1 ≤ M ∀n ∈N*.
Vậy dãy số (un) bị chặn dưới và không bị chặn trên nên không bị chặn.
b. Ta có: 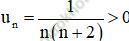 ∀ n ≥ 1.
∀ n ≥ 1.
⇒ (un) bị chặn dưới
![]()
⇒ (un) bị chặn trên.
Vậy (un) là dãy bị chặn.
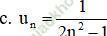
+ Ta có: 2n2 – 1 > 0 ∀ n ∈ N*
⇒ 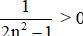 ∀ n ∈ N*.
∀ n ∈ N*.
⇒ (un) bị chặn dưới.
+ 2n2 – 1 ≥ 2.1 – 1 = 1
⇒ 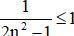 ∀ n ∈ N*
∀ n ∈ N*
⇒ (un) bị chặn trên.
Vậy (un) bị chặn.
d. un = sin n + cos n.
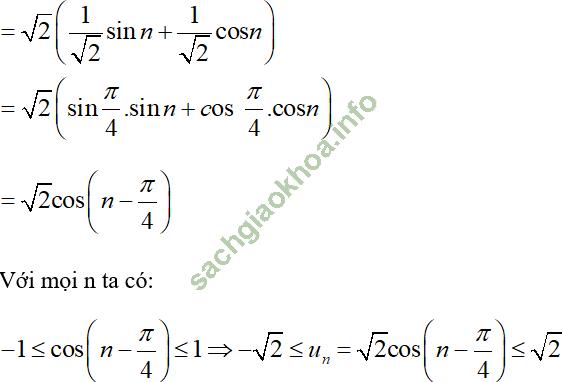
Vậy dãy số (un) bị chặn.
Kiến thức áp dụng:Dãy (un) được gọi là dãy số tăng nếu un + 1 > un ∀ n ∈ N*.
Dãy (un) được gọi là dãy số giảm nếu un + 1 < un ∀ n ∈ N*.