Viết phương trình tiếp tuyến của đường tròn tại 1 điểm, đi qua 1 điểm - Chuyên đề Toán 10

B. Ví dụ minh họa

Ví dụ 1: Cho đường tròn (C): (x - 3)² + (y - 1)² = 10. Phương trình tiếp tuyến của (C) tại điểm A (4; 4) là... ?

A. x - 3y + 8 = 0. B. x + 3y – 16 = 0. C. 2x - 3y + 5 = 0. D. x + 3y - 16 = 0.

Bài giải:

Đường tròn (C) có tâm I (3; 1). Gọi d là tiếp tuyến của đường tròn (C) tại điểm A; khi đó d và IA vuông góc với nhau.

⇒ = (1; 3) là vectơ pháp tuyến của d.

Vậy phương trình d là: 1 (x - 4) + 3 (y - 4) = 0

Hay x + 3y - 16 = 0.

Đáp án: D.

Ví dụ 2: Cho đường tròn (x - 3)² + (y + 1)² = 5. Phương trình tiếp tuyến của (C) song song với đường thẳng d: 2x + y + 7 = 0 là... ?

A. 2x + y = 0; 2x + y - 10 = 0 B. 2x + y + 1 = 0; 2x + y - 1 = 0

C. 2x - y + 1 = 0; 2x + y - 10 = 0 D. 2x + y = 0; x + 2y - 10 = 0

Bài giải:

Do tiếp tuyến cần tìm song song với đường thẳng d: 2x + y + 7 = 0 nên phương trình tiếp tuyến có dạng ∆: 2x + y + m = 0 với m ≠ 7.

Đường tròn (C) có tâm I (3; -1) và bán kính R = √ 5

Đường thẳng tiếp xúc với đường tròn (C) khi:

d (I, ∆) = R ⇔ = √ 5 ⇔ |5 + m| = 5

⇔

Vậy ∆₁: 2x + y = 0, ∆₂: 2x + y - 10 = 0

Đáp án: A.

Ví dụ 3. Viết phương trình tiếp tuyến ∆ của đường tròn (C): x² + y² - 4x - 4y + 4 = 0, biết tiếp tuyến đó đi qua điểm B (4; 6).

A. x - 4 = 0 hoặc 3x + 4y - 36 = 0 B. x - 4 = 0 hoặc y - 6 = 0.

C. y - 6 = 0 hoặc 3x + 4y - 36 = 0 D. x - 4 = 0 hoặc 3x - 4y + 12 = 0

Bài giải:

+ Đường tròn (C) có tâm I (2; 2) và bán kính R = = 2

+ Tiếp tuyến ∆:

⇒ Phương trình ∆: a (x - 4) + b (y - 6) = 0 hay ax + by - 4a - 6b = 0 (*)

+ Do ∆ là tiếp tuyến của đường tròn (C) nên d (I; ∆) = R

⇔ = 2 ⇔ |- 2a - 4b| = 2

⇔ |a + 2b| = ⇔ a² + 4ab + 4b² = a² + b²

⇔ 4ab + 3b² = 0 ⇔

+ Nếu b = 0; chọn a = 1 thay vào (*) ta được ∆: x - 4 = 0.

+ Nếu 4a = - 3b ta chọn a = 3 thì b = -4 thay vào (*) ta được: 3x - 4y + 12 = 0

Vậy có hai phương trình tiếp tuyến thỏa mãn là: x - 4 = 0 và 3x - 4y + 12 = 0.

Đáp án: D.

Ví dụ 4. Tìm phương trình tiếp tuyến d của đường tròn (C): (x + 2)² + (y + 2)² = 25 tại điểm M (2; 1).

A. d: -y + 1 = 0 B. d: 4x + 3y + 14 = 0

C. d: 3x - 4y - 2 = 0 D. d: 4x + 3y - 11 = 0

Bài giải:

+ Đường tròn (C) có tâm I (-2; -2) và bán kính R= 5.

+ Do đường thẳng d tiếp xúc với đường tròn taị điểm M nên hai đường thẳng d và IM vuông góc với nhau.

+ Đường thẳng d:

⇒ Phương trình (d): 4 (x - 2) + 3 (y - 1) = 0 hay 4x + 3y - 11 = 0

Đáp án: D.

Ví dụ 5. Cho đường tròn (C): (x - 1)² + (y + 2)² = 2. Lập phương trình tiếp tuyến d của (C) tại điểm A (3; -4).

A. d: x + y + 1 = 0 B. d: x - 2y - 11 = 0

C. d: x - y - 7 = 0 D. d: x - y + 7 = 0

Bài giải:

+ Đường tròn (C) có tâm I (1; -2).

+ Do đường thẳng d tiếp xúc với đường tròn tại điểm A (3; -4) nên đường thẳng d vuông góc với đường thẳng IA.

+ Phương trình đường thẳng (d):

⇒ Phương trình (d) là: 2 (x - 3) – 2 (y + 4) = 0

⇔ (d): 2x - 2y - 14 = 0 hay x - y - 7 = 0

Đáp án: C.

Ví dụ 6. Cho đường tròn (C) có phương trìn: (x + 1)² + (y - 1)² = 25 và điểm M (9; -4) . Gọi ∆ là tiếp tuyến của (C), biết ∆ đi qua M và không song song với các trục tọa độ. Tính khoảng cách từ điểm P (6; 5) đến ∆?

A. 2 B. 3 C. 4 D. 5

Bài giải:

+ Đường tròn (C) có tâm I (-1; 1) và bán kính R= 5.

+ Tiếp tuyến ∆:

⇒ Phương trình ∆: a (x - 9) + b (y + 4) = 0 hay ax + by – 9a + 4b = 0 (*)

+ Do ∆ là tiếp tuyến của đường tròn (C) nên d (I; ∆) = R

⇔ = 5 ⇔ |-10a + 5b| = 5

⇔ |-2a + b| =

⇔ 4a² - 4ab + b² = a² + b²

⇔ 3a² - 4ab = 0

⇔

+ Nếu a = 0 chọn b = 1 thay vào (*) ta được: y + 4 = 0 (loại) vì tiếp tuyến không song song với các trục tọa độ.

+ Nếu 3a = 4b, chọn a = 4 thì b = 3 ta được ∆: 4x + 3y - 24 = 0

⇒ Khoảng cách từ P (6; 5) đến đường thẳng ∆ là: d (P, ∆) = = 3

Đáp án: B.

Ví dụ 7. Có bao nhiêu đường thẳng đi qua gốc tọa độ O và tiếp xúc với đường tròn
(C): x² + y² - 2x + 4y - 11 = 0?

A. 0. B. 2. C. 1. D. 3.

Bài giải:

Đường tròn (C) có tâm I (1; -2) và bán kính R = = 4.

Độ dài OI = = √ 5

⇒ Điểm O nằm trong đường tròn nên không có tiếp tuyến nào của đường tròn kẻ từ O.

Đáp án: A.

Ví dụ 8. Cho đường tròn (C): (x - 3)² + (y + 3)² = 1. Qua điểm M (4; -3) có thể kẻ được mấy đường thẳng tiếp xúc với đường tròn (C)?

A. 0. B. 1. C. 2. D. Vô số.

Bài giải:

Thay tọa độ điểm M vào phương trình đường tròn (C) ta được:

(4 - 3)² + (-3 + 3)² = 1

⇒ Điểm M thuộc (C).

⇒ Có đúng 1 tiếp tuyến của đường tròn kẻ từ M.

Đáp án: B.

Ví dụ 9. Có mấy đường thẳng đi qua điểm N (-2; 0) tiếp xúc với đường tròn (C): (x - 2)² + (y + 3)² = 4?

A. 0. B. 1. C. 2. D. Vô số.

Bài giải:

Đường tròn (C) có tâm I (2; -3) và bán kính R = 2.

Độ dài IN = = 5 > R

⇒ Điểm N nằm ngoài đường tròn (C) => Qua điểm N kẻ được hai tiếp tuyến đến đường tròn (C).

Đáp án: C.

Ví dụ 10. Lập phương trình tiếp tuyến ∆ của đường tròn (C): (x - 1)² + (y + 2)² = 8, biết tiếp tuyến đi qua điểm A (5; -2).

A. x - 5 = 0. B. x + y - 3 = 0 hoặc x - y 7 = 0.

C. x- 5= 0 hoặc x + y - 3 = 0. D. y + 2 = 0 hoặc x - y - 7 = 0.

Bài giải:

+ Đường tròn (C) có tâm I (1; -2) và bán kính R = 2√ 2

+ Tiếp tuyến ∆:

⇒ Phương trình ∆: a (x - 5) + b (y + 2) = 0 hay ax + by - 5a + 2b = 0.

+ Do ∆ là tiếp tuyến của đường tròn (C) nên d (I; ∆) = R

⇔ = 2√ 2 ⇔ |- 4a| = 2√ 2.

⇔ 16a² = 8 (a² + b²) ⇔ 8a² = 8b²

⇔

+ Nếu a = b; ta chọn a = 1 ⇒ b = 1. Khi đó phương trình tiếp tuyến ∆: x + y - 3 = 0

+ Nếu a = - b; chọn a = 1 thì b = - 1. Khi đó phương trình tiếp tuyến ∆: x - y - 7 = 0.

Vậy có hai tiếp tuyến thỏa mãn là x + y - 3 = 0 và x - y - 7 = 0

Đáp án: B.

Ví dụ 11: Cho đường tròn (C) có tâm I (1; 3), bán kính R= √ 52. Viết phương trình tiếp tuyến của đường tròn tại điểm M biết điểm M thuộc đường thẳng d: và tọa độ M nguyên?

A. x + 2y + 3 = 0 B. 2x + 5y + 21 = 0

C. 2x - 3y - 19 = 0 D. Đáp án khác

Bài giải:

+ Do điểm M thuộc đường thẳng d nên tọa độ M (3 + 2t; 1 - 4t).

+ Do điểm M thuộc đường tròn nên IM = R

⇔ IM² = R² ⇔ (2 + 2t)² + (2 + 4t)² = 52

⇔ 4t² + 8t + 4 + 16t² + 16t + 4 = 52

⇔ 20t² + 24t – 44 = 0 ⇔ t = 1 hoặc t = -11/5 (loại).

+ Với t = 1 thì tọa độ M (5; -3).

⇒ Phương trình tiếp tuyến của đường tròn tại điểm M (5; -3):

(∆):

⇒ Phương trình tiếp tuyến: 2 (x - 5) – 3 (y + 3) = 0 hay 2x - 3y - 19 = 0

Đáp án: C.

C. Bài tập vận dụng

Câu 1: Phương trình tiếp tuyến d của đường tròn (C): x² + y² - 3x-y= 0 tại điểm N (1; -1) là:

A. d: x + 3y - 2 = 0 B. d: x - 3y + 4 = 0

C. d: x - 3y - 4 = 0 D. d: x + 3y + 2 = 0

Hiển thị lời giải

Đáp án: D

+ Đường tròn (C) có tâm I (3/2; 1/2).

+ Do đường thẳng d tiếp xúc với đường tròn (C) tại điểm N nên đường thẳng d vuông góc với đường thẳng IN.

+ Phương trình đường thẳng (d):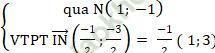

⇒ (d): 1 (x - 1) + 3 (y + 1) = 0 hay (d): x + 3y + 2 = 0

Câu 2: Cho đường tròn (C): x² + y² - 2x + 8y - 23 = 0 và điểm M (8; -3). Độ dài đoạn tiếp tuyến của (C) xuất phát từ M là:

A. 10 B. 2√ 10 C. √ 10/2 D. √ 10

Hiển thị lời giải

Đáp án: D

Đường tròn (C) có tâm I (1; -4) bán kính R = √ 40.

Độ dài IM = = √ 50 > R

⇒ Điểm M nằm ngoài đường tròn. Khi đó từ M sẽ kẻ được hai tiếp tuyến là MA và MB- trong đó A và B là hai tiếp điểm.

Theo tính chất hai tiếp tuyến cắt nhau ta có:

MA = MB = = √ 10

Vậy độ dài tiếp tuyến là: √ 10.

Câu 3: Cho đường tròn (C): x² + y² - 3x - y = 0. Phương trình tiếp tuyến của (C) tại M (1; -1) là:

A. x + 3y - 1 = 0 B. 2x - 3y + 1 = 0 C. 2x - y + 4 = 0 D. x + 3y + 2 = 0

Hiển thị lời giải

Đáp án: D

Đường tròn (C) có tâm I (3/2; 1/2 ).

Điểm M (1; -1) thuộc đường tròn (C).

Phương trình tiếp tuyến của đường tròn (C) tại điểm M là đường thẳng đi qua M và nhận vec tơ IM→ = (-1/2; -3/2) = -1/2 (1; 3) nên có phương trình:

1 (x - 1) + 3 (y + 1) = 0 hay x + 3y + 2 = 0

Câu 4: Cho đường tròn (x - 3)² + (y - 1)² = 10. Phương trình tiếp tuyến của (C) tại điểm A (4; 4) là

A. x - 3y + 5 = 0 B. x + 3y - 4 = 0 C. x - 3y + 16 = 0 D. x + 3y - 16 = 0

Hiển thị lời giải

Đáp án: D

Đường tròn (C) có tâm I (3; 1) và bán kính R = √ 10.

Tiếp tuyến của (C) tại A là đường thẳng qua A (4; 4) và nhận vecto IA→( 1; 3) là vectơ pháp tuyến của tiếp tuyến d.

Suy ra (d): 1 (x - 4) + 3 (y - 4) = 0 hay x + 3y - 16 = 0

Câu 5: Cho đường tròn (x - 2)² + (y - 2)² = 9. Phương trình tiếp tuyến của (C) đi qua điểm A (5; -1) là

A. x + y - 4 = 0 và x - y - 2 = 0. B. x = 5 và y = -1.

C. 2x - y - 3 = 0 và 3x + 2y - 3 = 0. D. 3x - 2y + 1 = 0 và 2x + 3y + 5 = 0

Hiển thị lời giải

Đáp án: B

+ Đường tròn (C) có tâm I (2; 2) và bán kính R = 3.

+ ∆ là tiếp tuyến cần tìm: đi qua A (5, -1) và nhận VTPT n→( A; B)

⇒ (∆): A (x - 5) + B (y + 1) = 0 (*)

+ Do ∆ là tiếp tuyến của (C) nên:

d (I; ∆) = R ⇔ = 3

⇔ |-3A + 3B| = 3

⇔ 9A² - 18AB + 9B² = 9A² + 9B²

⇔ 18AB = 0 ⇔

+ Với A =0; chọn B = 1 thay vào (*) ta được: y + 1 = 0

+ Với B = 0; chọn A = 1 thay vào (*) ta được: x - 5 = 0

Vậy có hai tiếp tuyến thỏa mãn là y + 1 = 0 và x - 5 = 0

Câu 6: Cho đường tròn (C): x² + y² + 2x - 6y + 5 = 0. Phương trình tiếp tuyến của (C) song song với đường thẳng d: x + 2y - 15 = 0 là

A. x + 2y = 0 và x + 2y - 10 = 0. B. x - 2y = 0 và x - 2y + 10 = 0.

C. x + 2y - 12 = 0 và x + 2y + 22 = 0 D. x + 2y + 3 = 0 và x + 2y + 7 = 0

Hiển thị lời giải

Đáp án: A

+ Đường tròn (C) có tâm I (-1; 3) và bán kính R = = √ 5

+ Do tiếp tuyến cần tìm song song với đường thẳng d: x + 2y- 15= 0 nên tiếp tuyến ∆ có dạng: x + 2y + m= 0 (m≠ -15).

+ ∆ là tiếp tuyến của (C) khi và chỉ khi:

d (I; ∆) = R ⇔ = √ 5 ⇔ |m + 5| = 5

⇔

⇒ Có hai tiếp tuyến thỏa mãn là: x + 2y = 0 và x + 2y - 10 = 0

Câu 7: Đường tròn (C) có tâm I (-1; 3) và tiếp xúc với đường thẳng d: 3x - 4y + 5 = 0 tại điểm H có tọa độ là

A. ( - 1/5; -7/5) B. (1/5; 7/5) C. ( 1/5; -7/5) D. ( - 1/5; 7/5)

Hiển thị lời giải

Đáp án: B

Do đường thẳng d là tiếp tuyến của đường tròn (C) tại điểm H nên IH vuông góc với đường thẳng d.

⇒ Đường thẳng IH:

⇒ Phương trình IH: 4 (x + 1) + 3 (y - 3) = 0 hay 4x + 3y - 5 = 0.

Do đường thẳng d và đường thẳng IH cắt nhau taị điểm H nên tọa độ điểm H là nghiệm hệ phương trình: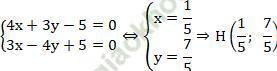

Câu 8: Cho đường tròn (C): x² + y² - 6x + 2y + 5 = 0 và đường thẳng
d: 2x + (m - 2)y – m - 7 = 0. Với giá trị nào của m thì d là tiếp tuyến của (C)?

A. m = 3 B. m = 15 C. m = 13 D. m = 3 hoặc m = 13.

Hiển thị lời giải

Đáp án: D

+ đường tròn (C) có tâm I (3; -1) và bán kính.

+ d là tiếp tuyến của (C) khi va chỉ khi:

d (I, d) = R ⇔ = √ 5 ⇔ |1 - 2m| = √ 5.

→ m² - 16m + 39 = 0 ⇔

Câu 9: Cho đường tròn (C) có tâm I (-1; 2), bán kính R = √ 29. Lập phương trình tiếp tuyến của đường tròn tại điểm M biết điểm M thuộc đường thẳng d:

và tọa độ M nguyên?

A. x + 2y + 3 = 0 B. 2x + 5y + 21 = 0

C. 3x + 5y - 8 = 0 D. Đáp án khác

Hiển thị lời giải

Đáp án: B

+ Do điểm M thuộc đường thẳng d nên tọa độ M (-2 + t; 3t).

+ Do điểm M thuộc đường tròn nên IM = R

⇔ IM² = R² ⇔ (t- 1)² + (3t - 2)² = 29

⇔ t² - 2t + 1 + 9t² - 12t + 4 = 29

⇔ 10t² – 14t – 24 = 0 ⇔ t = - 1 hoặc t = 12/5 (loại).

+ Với t = - 1 thì tọa độ M (- 3; - 3).

⇒ Phương trình tiếp tuyến của đường tròn tại điểm M (-3; -3):

(∆):

⇒ Phương trình tiếp tuyến: 2 (x + 3) + 5 (y + 3) = 0 hay 2x + 5y + 21 = 0.

Bài trước: Viết phương trình đường tròn đi qua 3 điểm (đường tròn ngoại tiếp tam giác) - Chuyên đề Toán 10 Bài tiếp: Vị trí tương đối của hai đường tròn, của đường thẳng và đường tròn - Chuyên đề Toán 10