Dạng 5: Nghiệm của phương trình bậc hai - Chuyên đề Toán 10

Ví dụ minh họa

Bài 1: Cho phương trình x² - 3x - 5 = 0. Tính tổng các lập phương hai nghiệm của phương trình?

Bài giải:

Phương trình: x² - 3x - 5 = 0 (*),

Có Δ = (-3)² - 4. (-5) = 29 > 0

=> PT (*) có hai nghiệm phân biệt x₁, x₂

Theo hệ thức Viet, ta có:

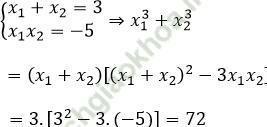
Bài 2: Giả sử phương trình x² - (2m + 1)x + m² + 2 = 0 (m là tham số) có hai nghiệm là x₁ và x₂. Tính giá trị biểu thức: P = 3x₁x₂ - 5 (x₁ + x₂) theo m.

Bài giải:

Theo định lý Viet, ta có:

Thay vào P, ta được P = 3 (m² + 2) - 5 (2m + 1) = 3m² - 10m + 1

Bài 3: Giả sử phương trình: 2x² - 4ax - 1 = 0 có hai nghiệm x₁, x₂. Tính giá trị của biểu thức T = |x₁ - x₂|

Bài giải:

Vì x₁, x₂ là hai nghiệm của phương trình: 2x² - 4ax - 1 = 0

Theo hệ thức Viet, ta có: x₁ + x₂ = - (-4a/2) = 2a và x₁.x₂ = -1/2 (1)

Mà T = |x₁ - x₂| ⇔ T² = (x₁ - x₂)² = (x₁ + x₂)² - 4x₁x₂ (2)

Từ (1) và (2) suy ra T² = (2a)² -4. (-1/2) = 4a² + 2

⇒ T = √ (4a² + 2) > 0

Bài 4: Cho hai phương trình x² - mx + 2 = 0 và x² + 2x - m = 0. Có bao nhiêu giá trị của m để một nghiệm của phương trình này và một nghiệm của phương trình kia có tổng là 3?

Bài giải:

Gọi x₀ là một nghiệm của phương trình: x² - mx + 2 = 0

Suy ra 3-x₀ là một nghiệm của phương trình: x² + 2x - m = 0

Khi đó, ta có hệ

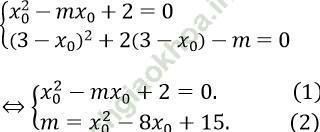
Thay (2) vào (1), ta được: x₀² - (x₀² - 8x₀ + 15)x₀ + 2 = 0

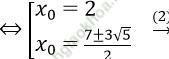cho ta 3 giá trị của m cần tìm

Bài 5: Gọi x₁, x₂ là hai nghiệm của phương trình: x² - 2 (m+1)x + m² + 2 = 0 (m là tham số). Xác định m để biểu thức P = x₁x₂ - 2 (x₁ + x₂) - 6 đạt giá trị nhỏ nhất.

Bài giải:

Ta có: Δ ' = (m + 1)² - (m² + 2) = 2m - 1

Để phương trình có hai nghiệm ⇔ Δ ' ≥ 0 ⇔ m ≥ 1/2. (*)

Theo định lý Viet, ta có:

Khi đó P = m² + 2 - 2 (2m + 2) - 6 = m² - 4m -8

Dấu " = " xảy ra < => m = 2.

Vậy với m = 2 biểu thức P đã cho đạt giá trị nhỏ nhất.

Bài 6: Gọi x₁, x₂ là hai nghiệm của phương trình: x² - (2m+1)x + m² + 1 = 0 (m là tham số). Tìm giá trị nguyên của m sao cho biểu thức có giá trị nguyên.

Bài giải:

Ta có: Δ = (2m + 1)² - 4 (m² + 1) = 4m - 3

Để phương trình có hai nghiệm ⇔ Δ ≥ 0 ⇔ m ≥ 3/4

Theo định lý Viet, ta có

Khi đó

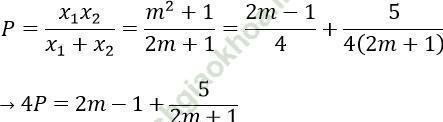
Do m ≥ 3/4 nên 2m + 1 ≥ 5/2

Để P ∈ Z thì ta phải có (2m + 1) là ước của 5 => 2m + 1 = 5 ⇔ m = 2

Thử lại với m = 2, ta được P = 1 (thỏa mãn)