Dạng 6: Phương trình chứa ẩn trong dấu giá trị tuyệt đối - Chuyên đề Toán 10

Ví dụ minh họa

Bài 1: Giải phương trình |3x - 2| = x² + 2x + 3

Bài giải:

Ta có: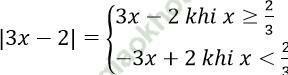

* Nếu x ≥ 2/3 ⇒ Pt đã cho ⇔ 3x - 2 = x² + 2x + 3

⇔ x² - x + 5 = 0 phương trình vô nghiệm

* Nếu x < 2/3 ⇒ Pt ⇔ -3x + 2 = x² + 2x + 3

⇔ x² + 5x + 1 = 0

⇔ x = (-5 ± √ 21)/2 hai nghiệm này đều thỏa mãn x < 2/3

Vậy nghiệm của phương trình đã cho là x = (-5 ± √ 21)/2

Bài 2: Giải phương trình |x³ - 1| = |x² - 3x + 2|

Bài giải:

Hai vế không âm bình phương hai vế ta có:

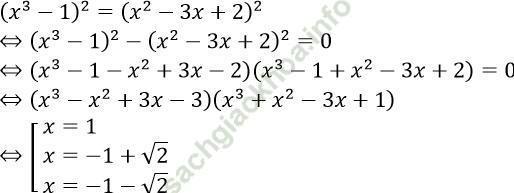
Vậy tập nghiệm của phương trình đã cho là: S = {1; -1 + √ 2; -1 - √ 2}

Bài 3: Giải phương trình: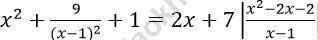

Bài giải:

TXĐ: D= R\ {1}

Phương trình đã cho < =>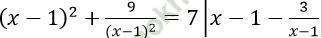

Đặt t = |x - 1 - 3/ (x-1)|

=>

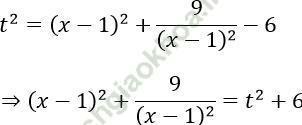
Phương trình trở thành: t² + 6 = 7t ⇔ t² - 7t + 6 = 0 ⇔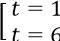

Với t = 1 ta có:

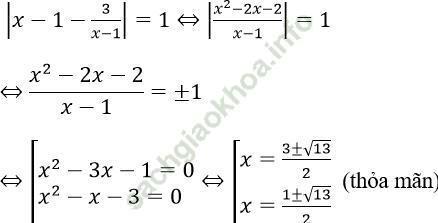
Với t = 6 ta có:

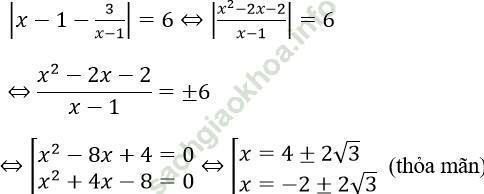
Vậy phương trình có nghiệm là:

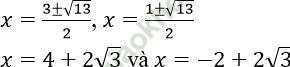
Bài 4: Giải phương trình: |2x - 5| + |2x² - 7x + 5| = 0

Bài giải:

Ta có:

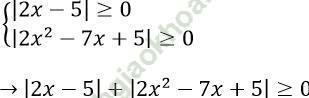
Dấu ''='' xảy ra < =>

Vậy tập nghiệm của phương trình là S = {5/2}

Bài 5: Phương trình (x + 1)² - 3|x + 1| + 2 = 0 có mấy nghiệm?

Bài giải:

Đặt t = |x + 1|, t ≥ 0

Phương trình trở thành t² - 3t + 2 = 0 ⇔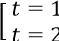

Với t = 1 ta có |x + 1| = 1 ⇔ x + 1 = ±1 ⇔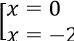

Với t = 2 ta có |x + 1| = 2 ⇔ x + 1 = ±2 ⇔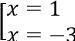

Vậy phương trình có nghiệm 4 nghiệm là x = -3, x = -2, x = 0 và x = 1

Bài trước: Bài tập về nghiệm của phương trình bậc hai - Chuyên đề Toán 10 Bài tiếp: Bài tập phương trình chứa ẩn trong dấu giá trị tuyệt đối - Chuyên đề Toán 10