Các dạng bài tập khác về đường tròn trong mặt phẳng - Chuyên đề Toán 10
Ví dụ 1: Cho đường tròn (C): x2 + y2 – 4x - 6y + 5 = 0. Hỏi có mấy điểm có tọa độ nguyên thuộc đường tròn?
A. 2 B. 5 C. 4 D. 7
Bài giải:
Xét phương trình (C) với ẩn y; x là tham số
y2 - 6y + (x2 - 4x + 5) = 0
Phương trình trên có nghiệm < => ∆' ≥ 0
⇔ 9 - x2 + 4x - 5 ≥ 0
⇔ x2 - 4x - 4 ≤ 0
⇔ 2 - √ 8 ≤ x ≤ 2 + √ 8
⇒ Các điểm M (x; y) thuộc (C) có hoành độ nguyên là 0; 1; 2; 3; 4 ta có:
| X | 0 | 1 | 2 | 3 | 4 |
| Y | 1 hoặc 5 | y không nguyên | y không nguyên | y không nguyên | 1 hoặc y = 5 |
Suy ra tồn tại 4 điểm thuộc (C) có tọa độ nguyên là: (0; 1); (0; 5); (4; 1) và (4; 5)
Đáp án: C.
Ví dụ 2: Xác định tọa độ điểm M thuộc (C): x2 + y2 – 4x - 6y + 11 = 0 sao cho MA lớn nhất, biết tọa độ của A (3; 2).
A. M (- 2; 8) B. M (9; 2) C. M (1; 4) D. M (3; 8)
Bài giải:
- Nhận xét: Đường tròn (C) có tâm I (2; 3).
- Thay tọa độ điểm A vào phương trình đường tròn ta được:
32 + 22 - 4.3 - 6.2 + 11 = 0 (đúng)
⇒ Điểm A thuộc đường tròn (C).
⇒ Để MA đạt lớn nhất thì MA là đường kính
⇒ M đối xứng với A qua I hay I là trung điểm của MA.
Tọa độ điểm M là: ![]() ⇒ M (1; 4)
⇒ M (1; 4)
Đáp án: C.
Ví dụ 3: Cho đường tròn (C): (x - 2)2 + (y - 3)2 = 5. Xác định trên
(C) điểm M sao cho
MB = 4 biết rằng B (1; 5)?
A. M (1; - 1) B. M (11/5; 13/5) C. M (-31/5; 13/5) D. Đáp án khác
Bài giải:
Gọi điểm M có tọa độ (x0; y0).
Vì M nằm trên đường tròn (C) => (x0 – 2)2 + (y0 - 3)2 = 5
Hay x02 - 4x0 + y02 - 6y0 + 8 = 0 (1)
Theo giả thiết BM = 4 nên BM2 = 16
⇔ (x0 - 1)2 + (y0 - 5)2 = 16
Hay x02 - 2x0 + y02 - 10y0 + 10 = 0 (2)
Lấy (2) - (1) ta được: 2x0 – 4y0 + 2 = 0
⇔ x0 - 2y0 + 1 = 0
⇔ x0 = 2y0 – 1
Thay vào (1) ta được:
( 2y0 - 1)2 – 2 (2y0 – 1) + y02 - 10y0 + 10 = 0
⇔ 5 y02 - 18y0 + 13 = 0
⇔ 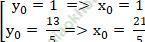
Vậy có hai điểm M thỏa mãn là M (1; 1) và M (21/5; 13/5).
Đáp án: D.
Ví dụ 4: Cho đường tròn (C): (x - 3)2 + (y - 2)2 = 5. Xác định điểm E thuộc đường tròn sao cho tam giác OEF vuông tại O, biết điểm F (4; - 2)?
A. E1 (2; 4) và E2 ( 4/5; 8/5) B. E1(1; - 4) và E2 (4/5; 8/5).
C. E1 (3; - 6) và E2 ( -9/5; 8/5) . D. E1(2; 4) và E2 ( 9/5; -7/5)
Bài giải:
+ Do tam giác OEF vuông tại O nên OE vuông OF.
+ Đường thẳng OE: 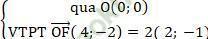
⇒ Phương trình OE: 2 (x - 0) – 1 (y - 0) = 0 hay 2x - y = 0.
+ Đường tròn và đường thẳng cắt nhau tại E nên tọa độ E là nghiệm hệ
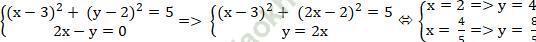
Vậy có hai điểm thỏa mãn là E1 (2; 4) và E2 (4/5; 8/5).
Đáp án: A.
Ví dụ 5: Cho đường tròn tâm O ngoại tiếp tam giác ABC biết tọa độ điểm B (2; m) và
C (n; 1). Xác định tọa độ điểm B? Biết rằng 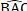 là góc nội tiếp chắn nửa đường tròn?
là góc nội tiếp chắn nửa đường tròn?
A. B (2; 1) B. B (2; 2) C. B (2; -1) D. B (2; -3)
Bài giải:
+ Do góc 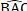 là góc nội tiếp chắn nửa đường tròn nên góc
là góc nội tiếp chắn nửa đường tròn nên góc 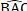 = 900.
= 900.
⇒ Tam giác BAC vuông tại A và BC là đường kính.
⇒ O (0; 0) là trung điểm của BC.
⇒ 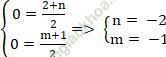
Suy ra, tọa độ điểm B (2; -1) và điểm C (-2; 1)
Đáp án: C.
Ví dụ 6: Cho đường tròn (C): x2 + y2 - 4x + 4y - 2 = 0; đường thẳng ∆: x + y - 2 = 0. Tìm trên d điểm A sao cho từ A kẻ được đúng một tiếp tuyến đến đường tròn (C)?
A. ( 1,1) B. ( 2; 0) C. ( 3; -1) D. (1; 1) hoặc (5; -3)
Bài giải:
+ Đường tròn (C) tâm I (2; -2) và bán kính R = 3.
- Nhận xét:
+ Nếu A nằm trong hình tròn (C) thì qua A không kẻ được tiếp tuyến nào đến đường tròn.
+ Nếu A nằm trên đường tròn (C) thì qua A kẻ được đúng một tiếp tuyến đến đường tròn.
+ Nếu A nằm bên ngoài hình tròn (C) thì qua A kẻ được hai tiếp tuyến nào với đường tròn.
Theo bài ra ta có: Từ điểm A kẻ được đúng một tiếp tuyến đến đường tròn (C) thì điểm A nằm trên đường tròn.
⇒ A là giao điểm của đường tròn (C) và đường thẳng d. Nên tọa độ A là nghiệm hệ:
Giải (*):
(*) ⇔ 4 - 4y + y2 + y2 – 8 + 4y + 4y - 2 = 0
⇔ 2y2 + 4y - 6 = 0
⇔ 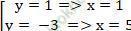
Vậy có 2 điểm A thỏa mãn đề bài là (1; 1) và (5; -3)
Đáp án: D.
Ví dụ 7. Trong mặt phẳng Oxy, đường tròn (C) có phương trình: x2 + y2 - 2x + 4y + 4 = 0, tâm I và điểm M (- 1; - 3). Lập phương trình đường thẳng ∆ đi qua M và cắt (C) tại 2 điểm phân biệt A, B sao cho tam giác IAB có diện tích lớn nhất.
A. x - y - 2 = 0 và x - 7y - 20 = 0 B. x + 2y - 7 = 0 và x - 3y - 20 = 0
C. 2x + y - 3 = 0 và x - 7y - 20 = 0 D. x - 4y = 0 và x + 2y - 20 = 0
Bài giải:
+ Đường tròn (C), tọa độ tâm I (1; -2); bán kính R = 1
+ Đường thẳng ∆: 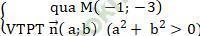
⇒ Phương trình ∆: a (x + 1) + b (y + 3) = 0 (*)
+ Do A và B là 2 điểm thuộc đường tròn (C) nên IA = IB = R = 1
Diện tích tam giác IAB là:
SIAB = 1/2 IA. IB. sin (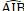 ) = 1/2.1.1. sin (
) = 1/2.1.1. sin (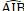 ) ≤ 1/2
) ≤ 1/2
⇒ SIAB lớn nhất < => 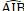 = 900 ⇒ IH =
= 900 ⇒ IH = 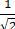 với H là hình chiếu I lên Δ
với H là hình chiếu I lên Δ
=> d (I; Δ) = IH = 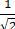
⇔ 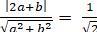
⇔ 7a2 + 8ab + b2 = 0
⇔ 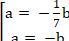
+ Nếu a = - 1/7b. Chọn b = - 7 => a = 1 thay vào (*) ta được phương trình đường thẳng ∆:
1 (x + 1) – 7 (y + 3) = 0 hay x - 7y - 20 = 0
+ Nếu a = - b; chọn a = 1; b = -1 thay vào (*) ta được phương trình đường thẳng ∆ là:
1 (x + 1) - 1. (y + 3) = 0 hay x - y - 2 = 0
Vậy có 2 đường thẳng thỏa mãn yêu cầu đề bài là: x - y - 2 = 0 và x - 7y - 20 = 0.
Đáp án: A
Ví dụ 8. Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường tròn (C): x2 + y2 – 4x - 6y = 0 và (C’): x2 + y2 + 4x = 0. Một đường thẳng đi qua giao điểm của (C) và (C') lần lượt cắt lại (C) và (C') tại M và N. Lập phương trình đường thẳng khi MN đạt giá trị lớn nhất.
A. 2x - y = 0 và x + 4y + 12 = 0 B. 3x - 4y = 0 và 3x - 4y + 12 = 0
C. x + y - 10 = 0 và 3x - y + 12 = 0 D. Tất cả sai
Bài giải:
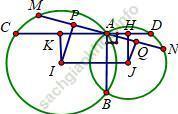
+ Đường tròn (C) có tâm I (2; 3) và bán kính R = √ 13
+ Đường tròn (C') có tâm J (- 2; 0) và bán kính R’ = 2.
⇒ IJ = 5 => |R - r| < IJ < R + r
⇒ Đường tròn (C) cắt (C') tại hai điểm A, B
+ Xétđường thẳng ∆ bất kì qua A cắt (C) và (C') tại M và N. Gọi ∆' là đường thẳng qua A vuông góc với AB, cắt (C), (C') lần lượt tại C và D. Gọi K, H lần lượt là là hình chiếu của I, J lên ∆'. Gọi P, Q lần lượt là là hình chiếu của I, J lên ∆.
=> Ta có: MN = 2PQ ≤ 2IJ = 2KH = CD
⇒ MNmax = CD.
+ Tọa độ A, B là nghiệm của hệ: 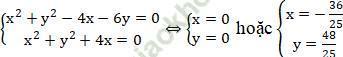
Từ đó suy ra có hai đường thẳng thỏa mãn:
- (∆1): 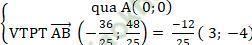
⇒ Phương trình: 3 (x - 0) – 4 (y - 0) = 0 hay 3x - 4y = 0
- (∆2): 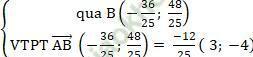
⇒ Phương trình: 3 (x + 36/25) - 4 (y - 48/25) = 0 hay 3x - 4y + 12 = 0
Vậy có 2 đường thẳng thỏa mãn đề bài là: 3x - 4y = 0 và 3x - 4y + 12 = 0.
Đáp án: B.
C. Bài tập vận dụng
Câu 1: Cho phương trình đường cong: x2 + y2 + (m + 2)x - (m + 4)y + m + 1 = 0 (*). Xác đinh mệnh đề sai trong các đáp án sau?
A. ( Cm) là phương trình của đường tròn với mọi m.
B. Tập hợp tâm các đường tròn khi m thay đổi là đường thẳng x + y - 1 = 0
C. Khi m thay đổi họ các đường tròn (Cm) có đúng một điểm cố định.
D. Họ các đường tròn (Cm) luôn đi qua điểm M (1; 2) với mọi m.
Đáp án: C
+ Ta có a2 + b2 - c = 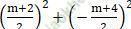 - m - 1 =
- m - 1 = 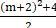 > 0
> 0
Suy ra (*) là phương trình đường tròn với mọi m
+ Đường tròn có tâm I: 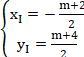 suy ra xI + yI - 1 = 0
suy ra xI + yI - 1 = 0
Vậy tập hợp tâm các đường tròn là đường thẳng ∆: x + y - 1 = 0
+ Gọi M (x0; y0) là điểm cố định mà họ (Cm) luôn đi qua.
Khi đó ta có: x02 + y02 + (m + 2)x0 - (m + 4)y0 + m + 1 = 0, ∀m
⇔ (x0 - y0 - 1)m + x02 + y02 + 2x0 - 4y0 + 1 = 0, ∀m
⇔ 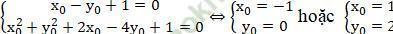
Vậy có hai điểm cố định mà họ (Cm) luôn đi qua với mọi m là A (- 1; 0) và M (1; 2)
Câu 2: Cho hai điểm A (8; 0) và B (0; 6). Viết phương trình đường tròn nội tiếp tam giác OAB?
A. (x - 2)2 + (y - 2)2 = 4 B. (x - 2)2 + (y + 2)2 = 1
C. ( x - 1)2 + (y + 1)2 = 1 D. (x - 2)2 + (y - 2)2 = 9
Đáp án: A
Ta có: OA = 8; OB = 6 và AB = 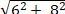 = 10.
= 10.
Mặt khác 1/2 OA. OB = pr (vì cùng bằng diện tích tam giác ABC)
Suy ra r = ![]() = 2
= 2
Gọi I là tâm đường tròn nội tiếp tam giác OAB
⇒ đường tròn tiếp xúc với hai trục tọa độ nên |a| = |b| = r = 2
Mà đường tròn có tâm thuộc góc phần tư thứ nhất nên a > 0; b > 0
⇒ a = b = r = 2
Vậy tâm đường tròn nội tiếp tam giác OAB là I (2; 2) bán kính đường tròn nội tiếp là
r = 2.
Vậy phương trình đường tròn nội tiếp tam giác OAB là
(x - 2)2 + (y – 2)2 = 4
Câu 3: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d1: √ 3x + y = 0 và
d2: √ 3x - y = 0. Gọi (C) là đường tròn tiếp xúc với d1 tại A, cắt d2 tại hai điểm B, C sao cho tam giác ABC
vuông tại B. Viết phương trình của (C), biết tam giác ABC có diện tích bằng 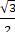 và điểm A có hoành độ dương.
và điểm A có hoành độ dương.
A. (x - 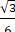 )2 + (y +
)2 + (y +  )2 = 4
B. (x +
)2 = 4
B. (x + 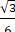 )2 + (y +
)2 + (y +  )2 = 1
)2 = 1
C. (x + 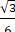 )2 + (y -
)2 + (y -  )2 = 1
D. (x -
)2 = 1
D. (x - 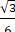 )2 + (y -
)2 + (y -  )2 = 1
)2 = 1
Đáp án: B
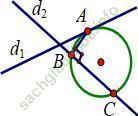
+ Vì A ∈ d1 ⇒ A (a; -√ 3a), a > 0; B, C ∈ d2 ⇒ B (b; √ 3b), C (c; √ 3c)
Suy ra AB→(b - a; √ 3 (a + b)), AC→(c - a; √ 3 (c + a))
+ Tam giác ABC vuông tại B do đó AC là đường kính của đường tròn C.
Do đó AC ⊥ d1 ⇒ AC→.u1→ = 0 ⇔ -1. (c - a) + √ 3. √ 3 (a + c) = 0 ⇔ 2a + c = 0 (1)
AB ⊥ d2 ⇒ AB→.u2→ = 0 ⇔ 1. (b - a) + 3 (a + b) = 0 ⇔ 2b + a = 0 (2)
Mặt khác SABC = 1/2 d (A; d2). BC ⇒ 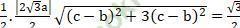
Từ (1), (2) suy ra 2 (c - b) = - 3a thế vào (3) ta được a|-3a| = 1
⇔ a = 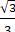
Do đó b = - 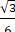 , c = -
, c = - ![]()
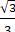 ; -1), C (-
; -1), C (- 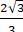 ; -2)
; -2)
Suy ra (C) nhận I (- 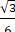 ; -
; -  ) là trung điểm AC làm tâm và bán kính là R =
) là trung điểm AC làm tâm và bán kính là R = 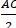 = 1
= 1
Vậy phương trình đường tròn cần tìm là (C): (x + 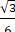 )2 + (y +
)2 + (y +  )2 = 1
)2 = 1
Câu 4: Trong mặt phẳng Oxy cho tam giác ABC, hai cạnh AB; AC theo thứ tự có phương trình x + y - 2 = 0 và x + 3y - 4 = 0. Cạnh BC có trung điểm M (- 1; 1). Xác định tâm của đường tròn ngoại tiếp tam giác ABC.
A. ( - 5; - 7) B. ( 4; - 3) C. ( - 7; 3) D. (1; 3)
Đáp án: A
+ Hai đường thẳng AB và AC cắt nhau tại A nên tọa độ điểm A là nghiệm hệ
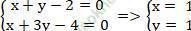 ⇒ A (1; 1)
⇒ A (1; 1)+ Gọi P là trung điểm của AC. Khi đó MP// AB (vì MP là đường trung bình của tam giác).
⇒ Đường thẳng MP có dạng: x + y + c = 0 (c ≠ - 2)
Mà M (- 1; 1) thuộc MP nên: - 1 + 1 + c = 0 ⇔ c = 0
Phương trình MP: x + y = 0.
+ MP và AC cắt nhau tại P ta tìm được P (- 2; 2).
+ Mà P là trung điểm của AC nên tọa độ điểm C (- 5; 3).
+ Điểm M là trung điểm BC nên tọa độ điểm B: 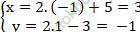
+ Lập phương trình đường tròn đi qua ba điểm A; B và C.
Gọi phương trình đường tròn là: x2 + y2 – 2ax - 2by + c = 0 (a2 + b2 - c > 0)
Do A; B và C thuộc đường tròn nên: 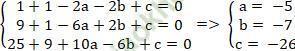
Vậy phương trình đường tròn cần tìm có tâm là I (- 5; - 7)
Câu 5: Lập phương trình đường tròn nội tiếp tam giác ABC tạo bởi ba đường thẳng
4x - 3y - 65 = 0; 7x - 24y + 55 = 0; 3x + 4y - 5 = 0.
A. (x - 10)2 + y2 = 25 B. (x - 1)2 + (y - 2)2 = 25
C. (x - 10)2 + (y - 2)2 = 25 D. Tất cả sai
Đáp án: A
+ Gọi ABC là tam giác đã cho với các cạnh là:
AB: 4x - 3y - 65 = 0; BC: 7x - 24y + 55 = 0; CA: 3x + 4y - 5 = 0
+ Suy ra A (11; - 7); B (23; 9); C (- 1; 2)
Ta có: AB→( 12; 16); AC→( - 12; 9)
⇒ AB→.AC→ = 12. ( - 12) + 16.9 = 0
⇒ AB và AC vuông góc với nhau nên tam giác ABC vuông ở A.
Ta có AB = 20; BC = 25; CA = 15
⇒ S = 1/2 . AB. AC = 150.
+ Lại có: S = p. r với p = 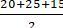 = 30 là nửa chu vi của tam giác ABC.
= 30 là nửa chu vi của tam giác ABC.
⇒ r =  = 5.
= 5.
+ Tâm đường tròn nội tiếp tam giác ABC là I (x; y) suy ra khoảng cách từ tâm I đến đường thẳng đã cho đều bằng r = 5 nên ta có:
5 = 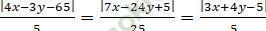
Giải hệ này ta tìm được I (10; 0)
Vậy phương trình đường tròn cần tìm là: (x - 10)2 + y2 = 25.
Câu 6: Trong mặt phẳng với hệ tọa độ Oxy, cho điểm M (2; 1) và đường thẳng
∆: x - y + 1 = 0. Viết phương trình đường tròn đi qua M cắt ở 2 điểm A, B phân biệt sao cho tam giác MAB vuông tại M và có diện tích bằng 2.
A. (x + 2)2 + (y - 2)2 = 2 B. (x - 1)2 + (y - 2)2 = 2
C. (x - 1)2 + (y + 3)2 = 16 D. (x - 5)2 + (y - 2)2 = 4
Đáp án: B
+ Đường tròn (C) tâm I (a, b) bán kính R có phương trình: (x - a)2 + (y - b)2 = R2
+ Tam giác MAB vuông tại M nên AB là đường kính và AB = 2R.
suy ra ∆ qua I do đó: a - b + 1 = 0 (1)
Hạ MH ⊥ AB có MH = d(M, ∆) = 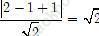
+ Diện tích tam giác MAB là:
SMAB = 1/2 MH. AB ⇔ 2 = 1/2 . 2R. √ 2 ⇔ R = √ 2
Vì đường tròn qua M nên (2 - a)2 + (1 - b)2 = 2 (2)
Ta có hệ: 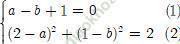
Giải hệ được a = 1; b = 2. Vậy (C) có phương trình: (x - 1)2 + (y - 2)2 = 2
Câu 7: Cho đường thẳng ∆: x - y + 1 = 0 và đường tròn (C): x2 + y2 – 4x + 2y - 4 = 0 Viết phương trình đường thẳng ∆' vuông góc với ∆ và cắt đường tròn tại hai điểm phân biệt sao cho khoảng cách của chúng là lớn nhất.
A. x + y - 2 = 0 B. x + y - 1 = 0 C. x + y = 0 D. x + y + 2 = 0
Đáp án: B
+ Đường tròn (C): tâm I (2; - 1) bán kính R = 3.
+ Vì vuông góc với và cắt đường tròn tại hai điểm phân biệt sao cho khoảng cách của chúng là lớn nhất nên vuông góc với và đi qua tâm I của đường tròn (C).
+ Đường thẳng ∆': 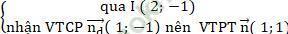
⇒ Phương trình ∆’: 1 (x - 2) + 1 (y + 1) = 0 hay x + y - 1 = 0
Vậy phương trình đường thẳng cần tìm là ∆’: x + y - 1 = 0.
Câu 8: Cho đường tròn (C): x2 + y2 – 2x + 4y - 4 = 0 có tâm I và đường thẳng ∆. Biết rằng đường thẳng ∆ cắt đường tròn (C) tại hai điểm phân biệt A, B. Xác định m để diện tích tam giác IAB là lớn nhất?
A. m = - 2 B. m = 1 C. m = - 4 D. m = 2
Đáp án: C
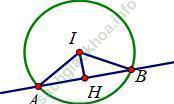
+ Đường tròn (C) có tâm I (1; -2), bán kính R = 3. ∆ cắt (C) tại hai điểm phân biệt khi và chỉ khi
d (I; Δ) < R ⇔ 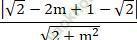 < 3 ⇔ 5m2 + 5m + 17 = 0 (đúng với mọi m)
< 3 ⇔ 5m2 + 5m + 17 = 0 (đúng với mọi m)
Vậy với mọi m đường thẳng ∆ luôn cắt đường tròn tại hai điểm phân biệt A; B.
+ Ta có IA = IB = R = 3 nên diện tích tam giác IAB là:
SIAB = 1/2
IA. IB. sin ![]()
Suy maxSIAB = 9/2 khi và chỉ khi:
sin 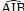 = 1 ⇔
= 1 ⇔ 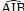 = 900
= 900
+ Gọi H là hình chiếu của I lên khi đó
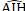 = 450 ⇒ IH = IA. cos450 =
= 450 ⇒ IH = IA. cos450 = 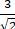
Ta có d (I; Δ) = IH ⇔ 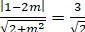
⇔ 2 - 8m + 8m2 = 18 + 9m2
⇔ m2 + 8m + 16 = 0 ⇔ m = - 4
Vậy với m = - 4 thỏa mãn yêu cầu bài toán.
Câu 9: Trong mặt phẳng Oxy, viết phương trình đường thẳng qua điểm O và cắt đường tròn (C): x2 + y2 – 2x + 6y - 15 = 0 (C) tại hai điểm A, B sao cho O là trung điểm của AB.
A. x + 3y = 0 B. x - 3y = 0 C. x - 2y = 0 D. 2x - y = 0
Đáp án: B
+ Đường tròn (C) có tâm I (1; -3) và bán kính R = 5.
+ Xét vị trí của điểm O và đường tròn (C):
OI = 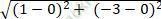 = √ 10 < R
= √ 10 < R
⇒ Điểm O nằm trong đường tròn.
+ Đường thẳng đi qua O và cắt (C) tại A, B với O là trung điểm AB
suy ra Δ ⊥ OI.
+ Đường thẳng AB: 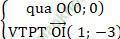
⇒ phương trình của AB: 1 (x - 0) – 3 (y - 0) = 0 hay x - 3y = 0.
Câu 10: Cho đường tròn (C): x2 + y2 = 4 và điểm M (2; 2). Có mấy đường thẳng qua M và cắt (C) tai hai điểm phân biệt A, B sao cho AB = 2.
A. 0 B. 1 C. 2 D. Vô số
Đáp án: C
+ Đường tròn (C) có tâm O (0; 0) và bán kính R = 2.
Đường thẳng cần tìm có dạng ∆: 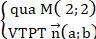
⇒ Phương trình ∆: a (x - 2) + b (y - 2) = 0
+ Gọi H là hình chiếu của O lên AB khi đó H là trung điểm AB nên AH = AB/2 = 1
⇒ OH =  = √ 3
= √ 3
+ Ta có OH = d (O; Δ) ⇔ √ 3 = 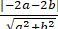
⇔ 3 (a2 + b2) = 4a2 + 8ab + 4b2 ⇔ a2 + 8ab + b2 = 0
⇔ a = (- 4 ± √ 15)b
Từ đó ta có hai đường thẳng thỏa mãn là:
Δ1: (-4 + √ 15)x + y + 6 - 2√ 15 = 0 và Δ2: (-4 - √ 15)x + y + 6 + 2√ 15 = 0