Dạng 11: Các dạng hệ phương trình đặc biệt - Chuyên đề Toán 10

Ví dụ minh họa

Bài 1: Giải hệ phương trình:

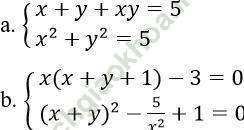
Bài giải:

a. Đặt S = x + y, P = xy (S² - 4P ≥ 0)

Ta có: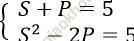

⇒ S² - 2 (5 - S) = 5

⇒ S² + 2S - 15 = 0

⇒ S = -5; S = 3

TH1: S = -5 ⇒ P = 10 (loại)

TH2: S = 3 ⇒ P = 2 (nhận)

Khi đó: x, y là nghiệm của phương trình: X² - 3X + 2 = 0

⇔ X = 1; X = 2

Vậy hệ có nghiệm là: (2; 1), (1; 2)

b. Điều kiện xác định: x ≠ 0

Hệ phương trình tương đương với

Vậy hệ phương trình có nghiệm (x; y) là (1; 1) và (2; -3/2)

Bài 2: Giải hệ phương trình:

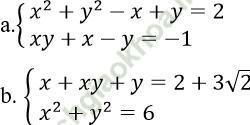
Bài giải:

a. Hệ phương trình đã cho tương đương

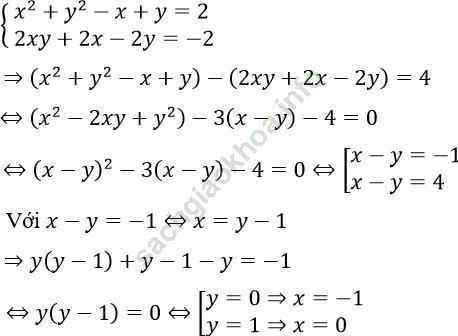
Với x - y = 4 ⇒ x = y + 4 ⇒ y (y + 4) + y + 4 - y = -1

⇔ y² + 4y + 5 = 0 (vô nghiệm)

Vậy nghiệm của hệ phương trình là (x; y) = {(0; 1), (-1; 0)}

b. Đặt S = x + y; P = xy, ta có hệ như sau:

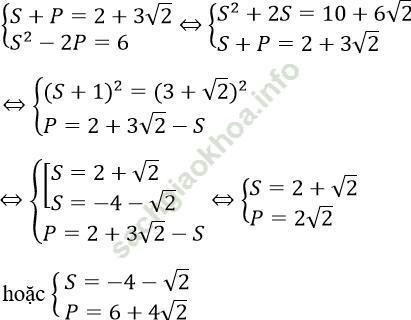
- Với S = 2 + √ 2; P = 2√ 2 ta có x, y là nghiệm phương trình:

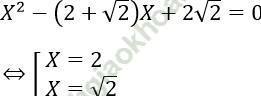
- Với S = -4 - √ 2; P = 6 + 4√ 2 ta có x, y là nghiệm phương trình:

X² + (4 + √ 2)X + 6 + 4√ 2 = 0 (vô nghiệm)

Vậy hệ có nghiệm (x; y) là (2; √ 2) và (√ 2; 2)

Bài 3: Giải hệ phương trình:

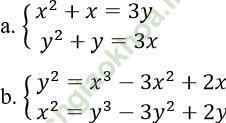
Bài giải:

a. Hệ phương trình đã cho tương đương:

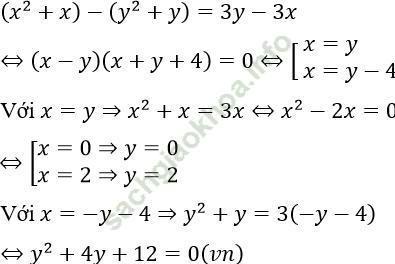
Vậy tập nghiệm của hệ phương trình là: (x; y) = {(0; 0), (2; 2)}

b. Trừ vế với vế của phương trình đầu và phương trình thứ hai ta được:

y² - x² = x³ - y³ - 3 (x² - y²) + 2 (x - y)

⇔ (x - y)(x² + xy + y² - 2x - 2y + 2) = 0

⇔ 1/2 (x - y)[x² + y² + (x + y - 2)²] = 0

⇔ x = y (vì x² + y² + (x + y - 2)² > 0)

Thay x = y vào phương trình đầu ta được:

x³ - 4x² + 2x = 0

⇔ x (x² - 4x + 2) = 0

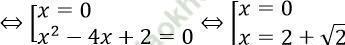
Vậy hệ phương trình có 3 nghiệm: (0; 0); (2+√ 2; 2+√ 2) và (2-√ 2; 2-√ 2)

Bài 4: Giải hệ phương trình:

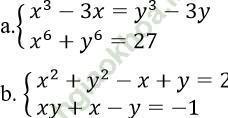
Bài giải:

a. Ta có: x³ - 3x = y³ - 3y

⇔ (x - y)(x² + xy + y²) - 3 (x - y) = 0

⇔ (x - y)(x² + xy + y² - 3) = 0

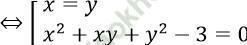
+) Khi x = y thì hệ có nghiệm.

+) Khi x² + xy + y² - 3 = 0

⇔ x² + y² = 3 - xy,

Ta có: x⁶ + y⁶ = 27

⇔ (x² + y²) (x⁴ - x²y² + y⁴) = 27

⇒ (3 - xy)[ (3 - xy)² - 3x²y²] = 27

⇔ 3 (xy)³ + 27xy = 0

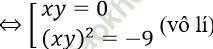
Vậy hệ phương trình đã cho có 2 nghiệm

b. Hệ phương trình đã cho tương đương

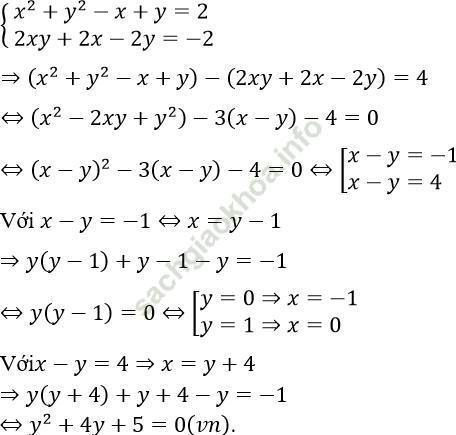
Bài 5: Giải hệ phương trình:

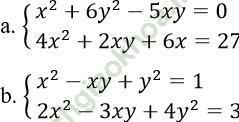
Bài giải:

a. Ta có:

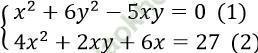
+) Nếu x = 0 thay vào (1)⇒ y = 0, thay vào (2) thấy (x; y) = (0; 0) là nghiệm của phương trình (2) nên không phải là nghiệm của hệ phương trình

+) Nếu x ≠ 0, đặt y = tx, thay vào hệ ta được:

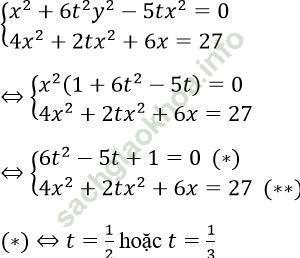
- Với t = 1/2 thay vào (**) ta được:

4x² + x² + 6x = 27

⇔ 5x² + 6x - 27 = 0

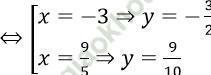
- Với t = 1/3 thay vào (**) ta được:

4x² + (2/3)x² + 6x = 27

⇔ 14x² + 18x - 81 = 0

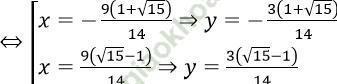
Vậy hệ phương trình có nghiệm (x; y) là:

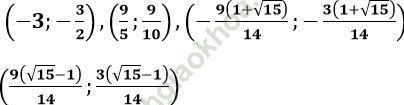
b. Dễ thấy x = 0 không thoả mãn hệ phương trình.

Với x ≠ 0, đặt y = tx, thay vào hệ ta được:

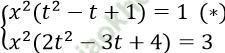
=> 3 (t² - t + 1) = 2t² - 3t + 4 ⇒ t = ±1

Thay vào (*) thì:

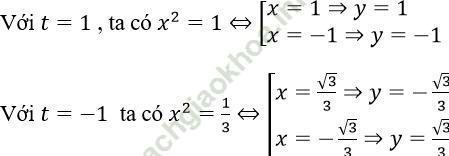
Vậy hệ phương trình có nghiệm (x; y) là (1/√ 3; (-1)/√ 3), ((-1)/√ 3; 1/√ 3), (-1; -1) và (1; 1)

Bài 6: Cho hệ phương trình 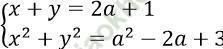. Tìm giá trị của a sao cho hệ có nghiệm (x; y) và tích x. y nhỏ nhất.

Bài giải:

Đặt S = x + y, P = xy (S² - 4P ≥ 0)

Ta có:

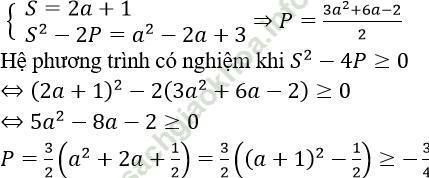
Đẳng thức xảy ra khi a = -1 (nhận)

Vậy với a = -1 thì hệ có nghiệm (x; y) và tích x. y là nhỏ nhất.

Bài 7: Xác định m để hệ phương trình: 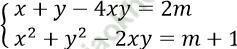có nghiệm.

Bài giải:

Hệ phương trình đã cho tương đương

(x² + y² - 2xy) - (x + y - 4xy) = m + 1 - 2m

⇔ (x + y)² - (x + y) + m - 1 = 0

Để hệ phương trình đã cho có nghiệm thì:

Δ ≥ 0

⇔ 1 - 4 (m - 1) ≥ 0

⇔ 5 - 4m ≥ 0

⇔ m ≤ 5/4

Từ phương trình thứ 2 ta có:

(x - y)² = m + 1

⇒ m + 1 ≥ 0

⇔ m ≥ -1

Vậy với m thỏa mãn điềuu kiện: -1 ≤ m ≤ 5/4 thì hệ phương trình đã cho có nghiệm.

Bài trước: Bài tập giải và biện luận hệ phương trình bậc nhất - Chuyên đề Toán 10 Bài tiếp: Bài tập các dạng hệ phương trình đặc biệt - Chuyên đề Toán 10