Bài tập các dạng hệ phương trình đặc biệt - Chuyên đề Toán 10
Câu 1. Điều kiện cần và đủ để hệ phương trình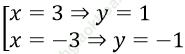 
có nghiệm là:
A. S2 – P < 0 B. S2 – P ≥ 0 C. S2 – 4P < 0 D. S2 – 4P ≥ 0
Bài giải:
Đáp án: D
Ta có: x, y là nghiệm phương trình: X2 - SX + P = 0
Hệ phương trình có nghiệm < => Δ = S2 - 4P ≥ 0
Câu 2. Cho hệ phương trình: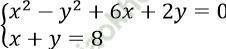
. Từ hệ phương trình này ta thu được phương trình nào sau đây?
A. x2 + 10x + 24 = 0
B. x2 + 16x + 20 = 0
C. x2 + x – 4 = 0
D. Một kết quá khác
Bài giải:
Đáp án: D
Ta có: y = 8 - x
⇒ x2 - (8 - x)2 + 6x + 2 (8 - x) = 0
⇒ 20x - 48 = 0
Câu 3. Nghiệm của hệ phương trình: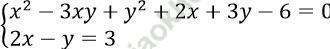 
là?
A. (2; 1) B. (3; 3) C. (2; 1), (3; 3) D. Vô nghiệm
Bài giải:
Đáp án: C
Ta có: y = 2x - 3
⇒ x2 - 3x (2x - 3) + (2x - 3)2 + 2x + 3 (2x - 3) - 6 = 0
⇒ -x2 + 5x - 6 = 0
⇒ x = 2; x = 3
+) Với x = 2 ⇒ y = 1
+) Với x = 3 ⇒ y = 3
Vậy hệ đã cho có 2 nghiệm (2; 1); (3; 3).
Câu 4. Tìm số nghiệm của hệ phương trình: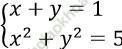 
A. 1 B. 2 C. 3 D. 4.
Bài giải:
Đáp án: B.
Ta có: y = 1 - x
⇒ x2 + (1 - x)2 = 5
⇒ 2x2 - 2x - 4 = 0
⇒ x = -1; x = 2
+) Với x = -1 => y = 2
+) Với x = 2 => y = -1
Vậy hệ phương trình đã cho có hai nghiệm (-1; 2); (2; -1)
Câu 5. Hệ phương trình: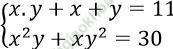 
A. có 2 nghiệm (2; 3) và (1; 5)
B. có 2 nghiệm (2; 1) và (3; 5)
C. có 1 nghiệm là (5; 6)
D. có 4 nghiệm (2; 3), (3; 2), (1; 5), (5; 1)
Bài giải:
Đáp án: D
Đặt S = x + y, P = xy (S2 - 4P ≥ 0)
Hệ phương trình tương đương
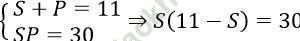
⇒ -S2 + 11S - 30 = 0
⇒ S = 5; S = 6
+) S = 5 => P = 6. Vậy hệ có 2 nghiệm (2; 3), (3; 2)
+) S = 6 => P = 5. Vậy hệ có 2 nghiệm (1; 5), (5; 1)
Câu 6. Nghiệm của hệ phương trình: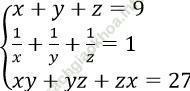 
A. (3; 3; 2) B. (1; 2; 3) C. (1; 1; 1) D. (3; 3; 3)
Bài giải:
Đáp án: D
Ta có: 1/x + 1/y + 1/z = 1
⇔ xy + yz + zx = xyz
⇒ xyz = 27
⇒ x, y, z là nghiệm của phương trình:
X3 - 9X2 + 27X - 27 = 0
⇔ X = 3
Vậy hệ phương trình có nghiệm là: (3; 3; 3)
Câu 7. Nghiệm của hệ phương trình: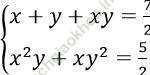 
là?
A. (3; 2); (-2; 1) B. (0; 1), (1; 0) C. (0; 2), (2; 0) D. (2; 1/2); (1/2; 2)
Bài giải:
Đáp án: D
Đặt: S = x + y, P = xy (S2 - 4P ≥ 0)
Ta có: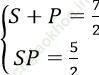 
⇒ S, P là nghiệm của phương trình: X2 - (7/2)X + 5/2 = 0
⇔ X = 1; X = 5/2
+) S = 1 => P = 5/2 (loại)
+) S = 5/2 => P = 1 thì x, y là nghiệm của phương trình X2 - (5/2)X + 1 = 0
⇔ X = 2; X = 1/2
Vậy hệ phương trình có 2 nghiệm (2; 1/2); (1/2; 2)
Câu 8. Nghiệm của hệ phương trình: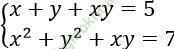 
là?
A. (2; 3) hoặc (3; 2)
B. (1; 2) hoặc (2; 1)
C. (-2; -3) hoặc (-3; -2)
D. (-1; -2) hoặc (-2; -1)
Bài giải:
Đáp án: B
Đặt S = x + y, P = xy (S2 - 4P ≥ 0)
Ta có: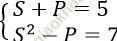 
⇒ S2 - (5 - S) = 7
⇒ S2 + S - 12 = 0
⇒ S = 3; S = -4
+) S = 3 ⇒ P = 2 thì x, y là nghiệm của phương trình X2 - 3X + 2 = 0
⇔ X = 1; X = 2
+) S = 2 ⇒ P = 3 (loại)
Vậy hệ pt đã cho có 2 nghiệm là (1; 2) hoặc (2; 1)
Câu 9. Nghiệm của hệ phương trình: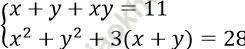 
là?
A. (3; 2), (2; 3)
B. (-3; -7), (-7; -3)
C. (3; 2); (-3; -7)
D. (3; 2), (2; 3), (-3; -7), (-7; -3)
Bài giải:
Đáp án: D
Đặt: S = x + y, P = xy (S2 - 4P ≥ 0)
Ta có: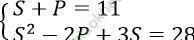 
⇒ S2 - 2 (11 - S) + 3S = 28
⇒ S2 + 5S - 50 = 0
⇒ S = 5; S = -10
+) S = 5 ⇒ P = 6 thì x, y là nghiệm của phương trình X2 - 5X + 6 = 0
⇔ X = 2; X = 3
+) S = -10 ⇒ P = 21 thì x, y là nghiệm của phương trình
X2 + 10X + 21 = 0 ⇔ X = -3; X = -7
Vậy hệ phương trình đã cho có nghiệm là: (3; 2), (2; 3), (-3; -7), (-7; -3)
Câu 10. Hệ phương trình: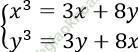 
có nghiệm là (x; y) với x ≠ 0 và y ≠ 0 là?
A. (-√ 11; -√ 11); (√ 11; √ 11)
B. (0; √ 11); (√ 11; 0)
C. (-√ 11; 0)
D. (√ 11; 0)
Bài giải:
Đáp án: A
Vậy hệ có nghiệm là: (-√ 11; -√ 11); (√ 11; √ 11).
Câu 11. Tìm các cặp nghiệm khác 0 của hệ phương trình: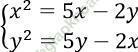 
A. (3; 3)
B. (2; 2), (3; 1), (-3; 6)
C. (1; 1), (2; 2), (3; 3)
D. (-2; -2), (1; -2), (-6; 3)
Bài giải:
Đáp án: A
Ta có: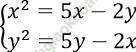 
⇒ x2 - y2 = 7x - 7y
⇒ (x - y)(x + y - 7) = 0
+) Với x = y => x2 - 3x = 0 ⇔ x = 0; x = 3
+) Với y = 7 - x => x2 - 7x + 14 = 0 (phương trình vô nghiệm)
Vậy hệ phương trình đã cho có nghiệm là: (3; 3)
Câu 12. Hệ phương trình: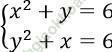 
có bao nhiêu nghiệm?
A. 6 B. 4 C. 2 D. 0
Bài giải:
Đáp án: C
Ta có: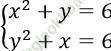 
⇒ x2 - y2 + y - x = 0
⇒ (x - y)(x + y - 1) = 0
+) x = y => x2 + x - 6 = 0
⇔ x = -3; x = 2
+) y = 1 - x => x2 - x + 7 = 0 (phương trình vô nghiệm)
Vậy hệ phương trình đã cho có hai nghiệm là: (-3; -3) và (2; 2).
Câu 13. Tìm số cặp nghiệm (x; y) của hệ phương trình: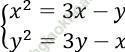 
?
A. 3 B. 2 C. 1 D. 0
Bài giải:
Đáp án: B
Ta có: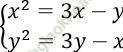 
⇒ x2 - y2 = 4x - 4yx ⇒ (x - y)(x + y - 1) = 0
+) x = y => x2 - 2x = 0 ⇔ x = 0; x = 2
+) y = 4 - x => x2 - 4x + 4 = 0 ⇔ x = 2
Vậy hệ phương trình có 2 nghiệm (0; 0), (2; 2)
Câu 14. Cho hệ phương trình: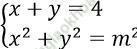 
Khẳng định nào sau đây là đúng?
A. Hệ phương trình có nghiệm với mọi m
B. Hệ phương trình có nghiệm ⇔ |m| ≥ √ 8
C. Hệ phương trình có nghiệm duy nhất ⇔ |m| ≥ 2
D. Hệ phương trình luôn vô nghiệm
Bài giải:
Đáp án: B
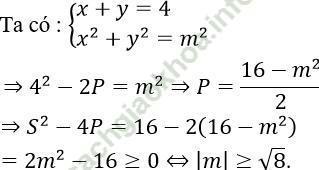
Câu 15. Cho hệ phương trình: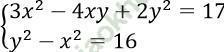 
Hệ thức biểu diễn x theo y rút ra từ hệ phương trình là?
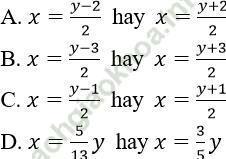
Bài giải:
Đáp án: D
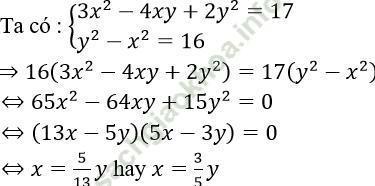
Câu 16. Tìm nghiệm của hệ phương trình: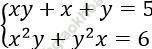 
A. (1; 2), (2; 1)
B. (0; 1), (1; 0)
C. (0; 2), (2; 0)
D. (2; 1/2), (1/2; 2)
Bài giải:
Đáp án: A
Đặt S = x + y, P = xy (S2 - 4P ≥ 0)
Ta có: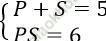 
⇒ S, P là nghiệm của phương trình: X2 - 5X + 6 = 0 ⇔ X = 2; X = 3
+) S = 2 => P = 3 (loại)
+) S = 3 => P = 2 thì x, y là nghiệm phương trình X2 - 3X + 2 = 0
⇔ X = 1; X = 2
Vậy hệ có 2 nghiệm là: (1; 2), (2; 1)
Câu 17. Hệ phương trình: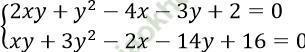 
có nghiệm là:
A. x bất kỳ, y = 2; x = 1, y = 3
B. x = 3, y = 2; x = 3, y = –1; x = 2, y = –1/2
C. x = 5, y = 2; x = 1, y = 3; x = 1/2, y = 2
D. x = 4, y = 2; x = 3, y = 1; x = 2, y = 1/2
Bài giải:
Đáp án: A
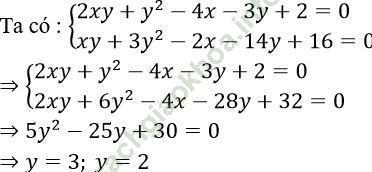
+) y = 3 => x = 1
+) y = 2 => x bất kỳ
Câu 18. Cho hệ phương trình: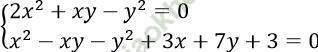 
Các cặp nghiệm (x; y) sao cho x, y đều là các số nguyên là:
A. (2; -2), (3; -3)
B. (-2; 2), (-3; 3)
C. (1; -1), (3; -3)
D. (-1; 1), (-4; 4)
Bài giải:
Đáp án: C
Đặt: 2x2 + xy - y2 = 0 (1)
x2 - xy - y2 +3x + 7y +3 = 0 (2)
Có: (1)⇔ (x + y)(2x - y) = 0
⇔
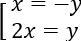
+) TH1: x = -y thay vào (2) được: x2 - 4x + 3 = 0 ⇔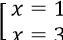
=> Hệ phương trình có hai nghiệm là (1; -1), (3; -3)
+) TH2: 2x = y thay vào (2) được: -5x2 + 17x + 3 = 0 phương trình nay không có nghiệm nguyên
Vậy các cặp nghiệm (x; y) sao cho x, y đều là các số nguyên là: (1; -1) và (3; -3)
Câu 19. Tìm số nghiệm của hệ phương trình sau: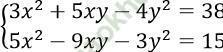 
A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. 4 nghiệm
Bài giải:
Đáp án: B
Nhận xét: x = 0 không thoả mãn hệ phương trình
Xét: x ≠ 0. Đặt x = ky và thay vào hệ ta được:
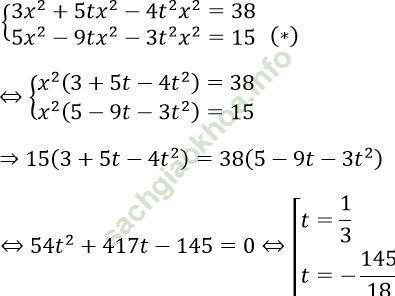
+) t = 1/3 thì (*) ⇔ x2 = 9 ⇔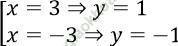 
+) t = -145/18 thì (*) ⇔ x2 = -15.108/12655: Phương trình vô nghiệm
Vậy: 
Câu 20. Số nghiệm của hệ phương trình: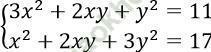 
là:
A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. 4 nghiệm
Bài giải:
Đáp án: D
Nhận xét: x = 0 không thoả mãn hệ phương trình
Với x ≠ 0, đặt y = kx, thay vào hệ ta được
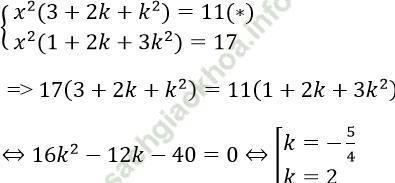
Thay vào (*) ta được:
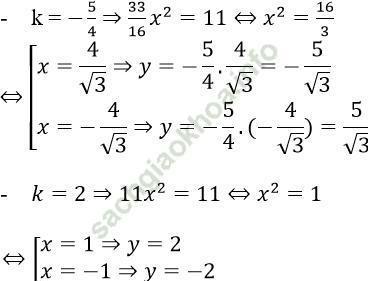
Vậy hệ phương trình có các nghiệm (x; y) là: (-4/√ 3,5/√ 3); (4/√ 3, -5/√ 3); (1; 2); (-1; -2)
Câu 21. Cho hệ phương trình: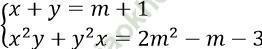 
và các mệnh đề:
(I) Hệ có vô số nghiệm khi = -1
(II) Hệ có nghiệm khi > 3/2
(III) Hệ có nghiệm với mọi
Các mệnh đề nào đúng?
A. Chỉ (I) B. Chỉ (II) C. Chỉ (III) D. Chỉ (I) và (III)
Bài giải:
Đáp án: D
Khi m = -1 thì hệ trở thành: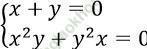 
⇒ Hệ có vô số nghiệm ⇒ (I) đúng
Ta có:
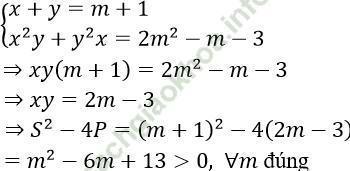
Câu 22. Tìm giá trị của m để hệ: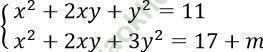 
có nghiệm.
A. m ≥ -6 B. m ≤ -6 C. m < -6 D. m ≥ 6
Bài giải:
Đáp án: A
Nhận xét: x = 0 không thoả mãn hệ phương trình.
Với x ≠ 0, đặt y = kx, thay vào hệ ta được
Ta có: 3 + 2k + k2 = (k + 1)2 + 2 > 0, ∀ k
⇒ (*) luôn có nghiệm x với mọi k vì vậy hệ ban đầu có nghiệm khi < => Phương trình (**) có nghiệm ẩn k.
+) m = 16: Phương trình (**) trở thành 44k + 88 = 0 ⇔ k = -2 => m = 16 thỏa mãn
+) m ≠ 16: Phương trình (**) có nghiệm ⇔ Δ 'k ≥ 0
⇔ (m + 6)2 - (m - 16)(m + 6) ≥ 0
⇔ 22 (m + 6) ≥ 0
⇔ m ≥ -6
Vậy hệ phương trình có nghiệm < => m ≥ -6
Câu 23. Hệ phương trình: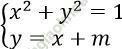 
có đúng 1 nghiệm khi và chỉ khi:
A. m = √ 2
B. m = -√ 2
C. m = √ 2 hoặc m = -√ 2
D. m tùy ý
Bài giải:
Đáp án: C
Ta có: x2 + (x + m)2 = 1
⇔ 2x2 + 2mx + m2 - 1 = 0 (*)
Hệ phương trình đã cho có đúng 1 nghiệm khi và chỉ khi phương trình (*) có đúng 1 nghiệm.
⇒ Δ ' = m2 - 2m2 + 2 = 0
⇔ m = ±√ 2
Bài trước: Dạng 11: Các dạng hệ phương trình đặc biệt - Chuyên đề Toán 10