Bài tập phương trình chứa ẩn trong dấu giá trị tuyệt đối - Chuyên đề Toán 10
Câu 1. Tập nghiệm S của phương trình |3x - 2| = 3 - 2x là?
A. S = {-1; 1} B. S = {-1} C. S = {1} D. S = {0}
Bài giải:
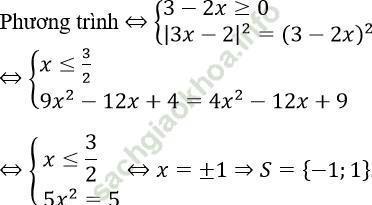
Đáp án: A
Câu 2. Tìm tập nghiệm S của phương trình: |2x - 1| = x - 3?
A. S = {4/3} B. S = ∅ C. S = {-2; 4/3} D. S = {-2}
Bài giải:
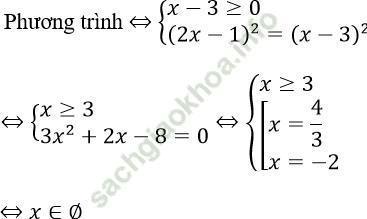
Vậy S = ∅
Đáp án: B
Câu 3. Tính tổng các nghiệm của phương trình |x2 + 5x + 4| = x + 4?
A. -12 B. -6 C. 6 D. 12
Bài giải:

Ta có tổng các nghiệm của pt là: 0 + (-2) + (-4) = -6
Đáp án: B
Câu 4. Tính tổng các nghiệm của phương trình 4x (x-1) = |2x-1| + 1?
A. 0 B. 1 C. 2 D. -2
Bài giải:
Ta có:
4x (x-1) = |2x-1| + 1
⇔ 4x2 - 4x - |2x-1| - 1 = 0 (1)
Đặt t = |2x-1|, t ≥ 0 ⇒ t2 = 4x2 - 4x + 1 ⇒ 4x2 - 4x = t2 - 1
Từ đó (1) ⇔ t2 - 1 - t - 1 = 0
⇔ t2 - t - 2 = 0
⇔ 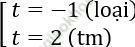
Với t = 2, ta có |2x - 1| = 2
⇔ 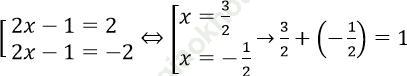
Câu 5. Phương trình: |2x - 4| + |x - 1| = 0 có mấy nghiệm?
A. 0 B. 1 C. 2 D. Vô số
Bài giải:
|2x - 4| + |x - 1| = 0 ⇔ 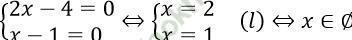
Câu 6. Gọi x1, x2 (x1 < x2) là hai nghiệm của phương trình |x2 - 4x - 5| = 4x - 17. Tính giá trị biểu thức P = x12 + x2
A. P = 16 B. P = 58 C. P = 28 D. P = 22
Bài giải:

Câu 7. Phương trình |2x + 1| = |x2 - 3x - 4| có bao nhiêu nghiệm?
A. 0 B. 1 C. 2 D. 4
Bài giải:
Phương trình:
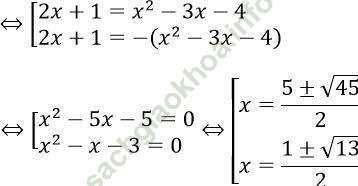
Câu 8. Nghiệm của phương trình: |x + 2| + |3x - 5| - |2x - 7| = 0, là?
A. ∀ x ∈ [-2; 5/3] B. x = -3 C. x = 3 D. x = 4
Bài giải:
+) Trường hợp 1: x ≤ -2
Phương trình thành: -x - 2 - 3x + 5 + 2x - 7 = 0
⇔ -2x = 4 ⇔ x = -2 (nhận)
+) Trường hợp 2: -2 ≤ x ≤ 5/3
Phương trình thành: x + 2 - 3x + 5 + 2x - 7 = 0 ⇔ 0x = 0 (luôn đúng)
Suy ra -2 ≤ x ≤ 5/3
+) Trường hợp 3: 5/3 ≤ x ≤ 7/2
Phương trình thành: x + 2 + 3x - 5 + 2x - 7 = 0 ⇔ 6x = 10 ⇔ x = 5/3 (nhận)
+) Trường hợp 4: x > 7/2
Phương trình thành: x + 2 + 3x -5 - 2x + 7 = 0 ⇔ 6x = -4
⇔ x = (-2)/3 (loại)
Vậy S = [-2; 5/3]
Đáp án: A
Câu 9. Cho phương trình: . Tìm nghiệm của phương trình.
A. x = 1 B. x = 3 C. x = 4 D. x = 5
Bài giải:
Điều kiện: 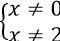
Phương trình < => x2 - 1 + |x + 1| = 2|x| (x - 2)
+) Trường hợp 1: x < -1
Phương trình trở thành:
x2 - 1 - x - 1 = 2 (-x)(x - 2)
⇔ 3x2 - 5x - 2 = 0
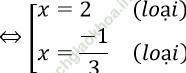
+) Trường hợp 2: -1 ≤ x ≤ 0
Phương trình thành: x2 - 1 + x + 1 = -2x (x - 2)
⇔ 3x2 - 3x = 0
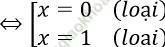
+) Trường hợp 3: x > 0
Phương trình thành x2 - 1 + x + 1 = 2x (x - 2)
⇔ x2 - 5x = 0
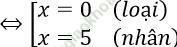
Đáp án: A
Câu 10. Phương trình 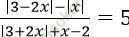 . Có các nghiệm là:
. Có các nghiệm là:
A. x = -1/8, x = -7
B. x = -21/9, x = 2/23
C. x = -22/9, x = 1/23
D. x = -23/9, x = 3/23
Bài giải:
Điều kiện: |3 + 2x| + x - 2 ≠ 0
Phương trình < => |3 - 2x| - |x| = 5|3 + 2x| + 5x - 10
+) Trường hợp 1: x < (-3)/2
Phương trình ⇔ 3 - 2x + x = -15 - 10x + 5x - 10
⇔ 4x = -28
⇔ x = -7 (nhận)
+) Trường hợp 2: (-3)/2 ≤ x ≤ 0
Phương trình ⇔ 3 - 2x + x = 15 + 10x + 5x - 10 ⇔ 16x = -2 ⇔ x = -1/8 (nhận)
+) Trường hợp 3: 0 < x < 3/2
Phương trình ⇔ 3 - 2x - x = 15 + 10x + 5x - 10
⇔ 18x = -2 ⇔ x = -1/9 (loại)
+) Trường hợp 4: x ≥ 3/2
Phương trình ⇔ -3 + 2x - x = 15 + 10x + 5x - 10
⇔ 14x = -8
⇔ x = -4/7 (loại)
Đáp án: A
Câu 11. Tập nghiệm của phương trình: |x - 2| = |3x - 5| (1) là tập hợp nào sau đây?
A. {3/2; 7/4} B. {-3/2; 7/4} C. {-7/4; -3/2} D. {-7/4; 3/2}
Bài giải:
Ta có
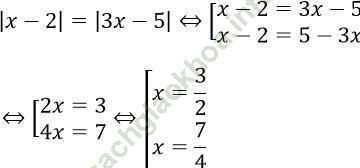
Câu 12. Tập nghiệm của phương trình: |x-2| = 2x-1 là
A. S = {-1; 1} B. S = {-1} C. S = {1} D. S = {0}
Bài giải:
Ta có |x - 2| = 2x - 1 ⇔ 2x - 1 ≥ 0 và 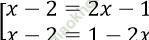
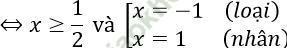
Vậy S = {1}
Đáp án: C
Câu 13. Nghiệm của phương trình: |3 - x| + |2x + 4| = 3 là?
A. x = (-4)/3 B. x = -4 C. x = 2/3 D. Vô nghiệm
Bài giải:
+) Trường hợp 1: x < -2
Phương trình ⇔ 3 - x - 2x - 4 = 3
⇔ 3x = -4
⇔ x = (-4)/3 (loại)
+) Trường hợp 2: -2 ≤ x ≤ 3
Phương trình ⇔ 3 - x + 2x + 4 = 3
⇔ x = -4 (loại)
+) Trường hợp 3: x > 3
Phương trình ⇔ x - 3 + 2x + 4 = 3
⇔ 3x = 2 ⇔ x = 2/3 (loại)
Vậy S = ∅
Đáp án: D
Câu 14. Số nghiệm của các phương trình (2x-1)2 - 3|2x-1| - 4 = 0 là:
A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. 4 nghiệm
Bài giải:
Đặt t = |2x - 1|, t ≥ 0
Phương trình trở thành t2 - 3t - 4 = 0 ⇔
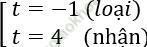
Với t = 4 ta có |2x - 1| = 4 ⇔ 2x - 1 = ±4 ⇔ x = 5/2 hoặc x = -3/2
Vậy phương trình có nghiệm là x = -3/2 và x = 5/2
Đáp án: B
Câu 15. Số nghiệm của các phương trình 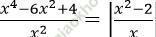 là:
là:
A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. 4 nghiệm
Bài giải:
ĐKXĐ: x ≠ 0. Đặt t = | (x2 - 2)/x|, t ≥ 0
Phương trình trở thành t2 - t - 2 = 0 ⇔ 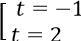
Với t = 2 ta có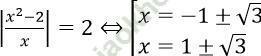
Vậy phương trình có nghiệm là x = -1 ± √ 3 và x = 1 ± √ 3
Đáp án: D