Dạng 7: Phương trình chứa ẩn ở mẫu - Chuyên đề Toán 10

Ví dụ minh họa

Bài 1: Giải phương trình: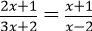

Bài giải:

TXĐ: D = R/ {-2/3; 2}

Phương trình đã cho < => (2x + 1)(x - 2) = (x + 1)(3x + 2)

⇔ 2x² - 4x + x - 2 = 3x² + 2x + 3x + 2

⇔ x² + 8x + 4 = 0 ⇔ x = -4 ± 2√ 3 (thỏa mãn điều kiện)

Vậy phương trình có 2 nghiệm là x = -4 ± 2√ 3

Bài 2: Giải phương trình: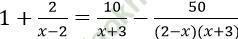

Bài giải:

TXĐ: D = R/ {-3; 2}

Phương trình < => (2 - x)(x + 3) - 2 (x + 3) = 10 (2 - x) - 50

⇔ x² - 7x - 30 = 0 ⇔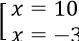

Đối chiếu với điều kiện ta có nghiệm X = -3 (loại). Vậy pt đã cho có 1 nghiệm là x = 10.

Bài 3: Giải phương trình: (1)

Bài giải:

TXĐ: D = R/ {-1; 1/2}

Từ (1) < =>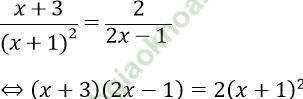

⇔ 2x² - x + 6x - 3 = 2x² + 4x + 2

⇔ x = 5 (thỏa mãn điều kiện)

Vậy phương trình có 1 nghiệm là x = 5

Bài 4: Giải phương trình: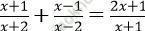

Bài giải:

TXĐ: D = R/ {±2; -1}.

Phương trình ⇔ (x + 1)²(x - 2) + (x - 1)(x + 1)(x + 2) = (2x + 1)(x - 2)(x + 2)

⇔ (x² + 2x + 1)(x - 2) + (x² - 1)(x + 2) = (2x + 1)(x² - 4)

⇔ x³ - 2x² + 2x² - 4x + x - 2 + x³ + 2x² - x - 2 = 2x³ - 8x + x² - 4

⇔ x² + 4x = 0 ⇔ 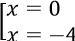(thỏa mãn điều kiện).

Vậy phương trình có 2 nghiệm là: x = -4 và x = 0

Bài 5: Giải phương trình: 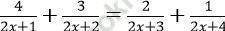(1)

Bài giải:

ĐKXĐ: x ∉ {-2; -3/2; -1; -1/2}

(1) tương đương với:

Vậy phương trình có 3 nghiệm là x = (-5 ± √ 3)/4 và x = -5/2

Bài trước: Bài tập phương trình chứa ẩn trong dấu giá trị tuyệt đối - Chuyên đề Toán 10 Bài tiếp: Bài tập phương trình chứa ẩn ở mẫu - Chuyên đề Toán 10