Dạng 2: Các phép toán trên tập hợp - Chuyên đề Toán 10

Cách giải bài tập các phép toán trên tập hợp hay, chi tiết

Phương pháp giải

* Hợp của 2 tập hợp:

x ∈ A ∪ B ⇔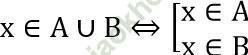

* Giao của 2 tập hợp:

x ∈ A ∩ B ⇔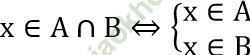

* Hiệu của 2 tập hợp:

x ∈ A \ B ⇔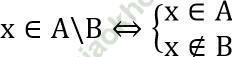

* Phần bù

Khi B ⊂ A thì A\B gọi là phần bù của B trong A, kí hiệu là CAB.

Ví dụ minh họa

Ví dụ 1: Cho A là tập hợp các học sinh lớp 10 đang học ở trường em, B là tập hợp các học sinh đang học môn Tiếng Anh của trường em. Hãy diễn đạt bằng lời các tập hợp sau: A ∪ B; A ∩ B; A \ B; B \ A.

Bài giải:

1. A ∪ B: Tập hợp các học sinh hoặc học lớp 10 hoặc học môn Tiếng Anh của trường em.

2. A ∩ B: Tập hợp các học sinh lớp 10 học môn Tiếng Anh của trường em.

3. A \ B: Tập hợp các học sinh học lớp 10 nhưng không học môn Tiếng Anh của trường em.

4. B \ A: Tập hợp các học sinh học môn Tiếng Anh của trường em nhưng không học lớp 10 của trường em.

Ví dụ 2: Cho hai tập hợp:

A = {x ∈ R | x² - 4x + 3 = 0};

B = {x ∈ R | x² - 3x + 2 = 0}.

Tìm A ∪ B; A ∩ B; A \ B; B \ A.

Bài giải:

Ta có: A = {1; 3} và B = {1; 2}

=> A ∪ B = {1; 2; 3}

A ∩ B = {1}

A \ B = {3}

B \ A = {2}

Ví dụ 3: Cho đoạn A = [-5; 1] và khoảng B = (-3; 2). Tìm A ∪ B; A ∩ B.

Bài giải:

A ∪ B= [-5; 2)

A ∩ B= (-3; 1]

Ví dụ 4: Cho A = {1,2,3,4,5,6,9}; B = {1,2,4,6,8,9} và C = {3,4,5,6,7}

a) Xác định hai tập hợp (A \ B) ∪ (B \ A) và (A ∪ B) \\ (A ∩ B). Hai tập hợp nhận được có bằng nhau không?

b) Tìm A ∩ (B \ C) và (A ∩ B) \ C. Hai tập hợp nhận được có bằng nhau không?

Bài giải:

a) Có: A = {1,2,3,4,5,6,9}; B = {1,2,4,6,8,9} và C = {3,4,5,6,7}

=> A \ B = {3,5}; B \ A = {8}

⇒ (A \ B) ∪ (B \ A) = {3; 5; 8}

A ∪ B = {1,2,3,4,5,6,8,9}

A ∩ B= {1,2,4,6,9}

⇒ (A ∪ B) \\ (A ∩ B)= {3; 5; 8}

Như vậy: (A \ B) ∪ (B \ A)= (A ∪ B) \\ (A ∩ B)

b) B \ C = {1,2,8,9}

⇒ A ∩ (B \ C) = {1,2,9}.

A ∩ B = {1,2,4,6,9}

⇒ (A ∩ B) \ C = {1,2,9}.

Như vậy: A ∩ (B \ C) = (A ∩ B) \ C

Ví dụ 5: Tìm tập hợp A, B biết: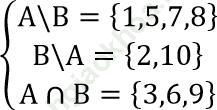

Bài giải:

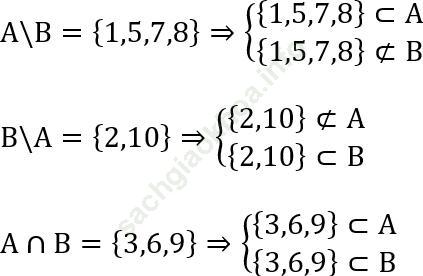
⇒ A = {1,5,7,8} ∪ {3,6,9} = {1,3,5,6,7,8,9}

B = {2,10} ∪ {3,6,9} = {2,3,6,9,10}

Ví dụ 6:

Cho hai đoạn A = [a; a + 2] và B = [b; b + 1]. Các số a, b cần thỏa mãn điều kiện gì để A ∩ B≠ ∅

Bài giải:

Điều kiện để A ∩ B= ∅ là:

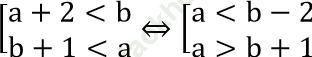
=> Điều kiện để A ∩ B ≠ ∅ là b - 2 ≤ a ≤ b + 1.

Bài trước: Dạng 1: Cách xác định tập hợp - Chuyên đề Toán 10 Bài tiếp: Dạng 3: Giải toán bằng biểu đồ Ven - Chuyên đề Toán 10