Bài tập phương trình chứa ẩn ở mẫu - Chuyên đề Toán 10

Câu 1. Tìm tập nghiệm của phương trình ?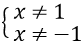

A. S = {1; 3/2} B. S = {1} C. S = {3/2} D. S = ∅

Bài giải:

Điều kiện: x ≠ 1

Phương trình < => 2x + 3/ (x - 1) = 3x/ (x - 1)

⇔ 2x (x - 1) + 3 = 3x

⇔ 2x² - 5x + 3 = 0

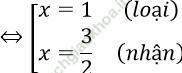
Vậy S = {3/2}

Đáp án: C

Câu 2. Gọi x₀ là nghiệm của phương trình: 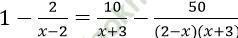. Mệnh đề nào sau đây là đúng?

A. x₀ ∈ (-5; -3)

B. x₀ ∈ [-3; -1]

C. x₀ ∈ (-1; 4)

D. x₀ ∈ [4; +∞)

Bài giải:

Điều kiện: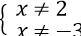

Phương trình ⇔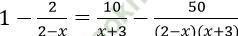

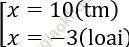
Đáp án: D

Câu 3. Tìm số nghiệm của phương trình: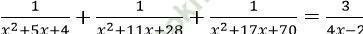

A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. 4 nghiệm

Bài giải:

Điều kiện: x ∉ {-10; -7; -4; -1; 1/2}

Phương trình ⇔

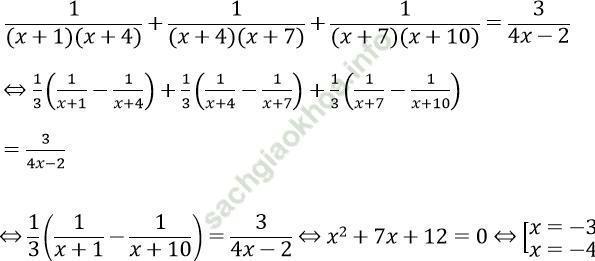
Đối chiếu với điều kiện thì nghiệm x = -4 (loại).

Vậy phương trình có nghiệm duy nhất là x = -3

Đáp án: A

Câu 4. Số nghiệm của phương trình: 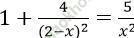là:

A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. 4 nghiệm

Bài giải:

TXĐ: D = R/ {0; 2}

Phương trình ⇔

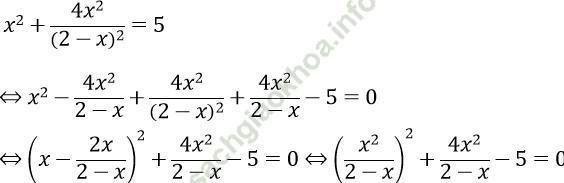
Đặt t = x²/ (2 - x), phương trình trên trở thành:

t² + 4t - 5 = 0 ⇔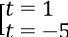

Với t = 1 ta có x²/ (2 - x) = 1 ⇔ x² + x - 2 = 0 ⇔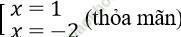

Với t = -5 ta có x²/ (2 - x) = -5 ⇔ x² - 5x + 10 = 0 (vô nghiệm)

Vậy phương trình có 2 nghiệm là x = -2 và x = 1

Đáp án: B

Câu 5. Tìm số nghiệm của phương trình: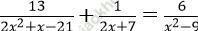

A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. 4 nghiệm

Bài giải:

TXĐ: D = R/ {±3; -7/2}

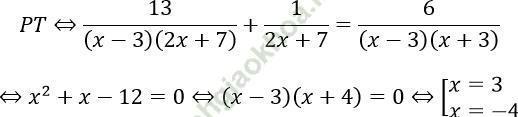
Đối chiếu với điều kiện thì nghiệm x = 3 (loại)

Vậy phương trình có 1 nghiệm duy nhất là: x = -4

Đáp án: A

Câu 6. Tìm số nghiệm của phương trình: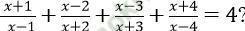

A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. 4 nghiệm

Bài giải:

Điều kiện: x ∉ {-3; -2; 1; 4}

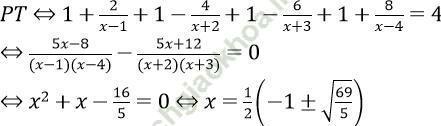
Đối chiếu với điều kiện phương trình có nghiệm 2 là x = (1/2)(-1 ± √ (69/5))

Đáp án: B

Câu 7. Số nghiệm của phương trình: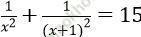

A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. 4 nghiệm

Bài giải:

Điều kiện: x ≠ -1; x ≠ 0

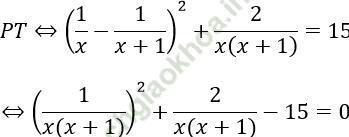
Đặt 1/ (x (x+1)) = t ta được phương trình t² + 2t - 15 = 0 ⇔ t = 3; t = -5

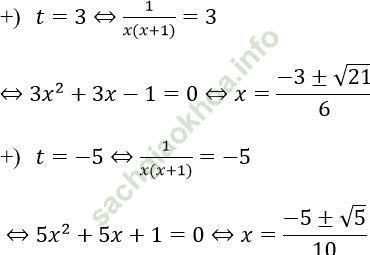
Đối chiếu với điều kiện thì phương trình có bốn nghiệm: x = (-3 ± √ 21)/6; x = (-5 ± √ 5)/10

Đáp án: D

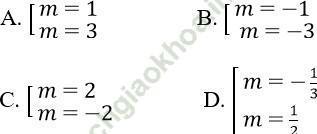
Câu 8. Cho phương trình: . Tìm m để phương trình vô nghiệm?

Bài giải:

Điều kiện: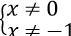

Phương trình < => x² + mx + x² - x - 2 = 2 (x² + x) ⇔ (m - 3)x = 2 (2)

Để phương trình (1) vô nghiệm thì Phương trình (2) vô nghiệm hoặc phương trình (2) có nghiệm duy nhất bằng 0 hoặc bằng -1

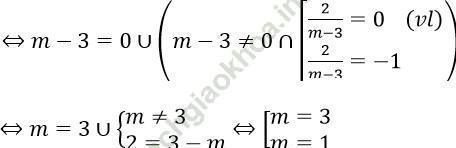
Đáp án: A

Câu 9. Tìm m để phương trình 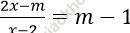vô nghiệm (m là tham số).

A. m = 3

B. m = 4

C. m = 3 ∨ m = 4

D. m = 3 ∨ m = -4

Bài giải:

Điều kiện: x ≠ 2

Phương trình < => 2x - m = mx - 2m - x + 2

⇔ (m - 3)x = m - 2 (2)

Để phương trình (1) vô nghiệm thì phương trình (2) vô nghiệm hoặc phương trình (2) có nghiệm duy nhất bằng 2

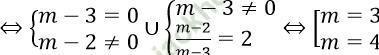
Đáp án: A

Câu 10. Phương trình: 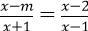có nghiệm duy nhất khi:

A. m ≠ 0

B. m ≠ -1

C. m ≠ 0 và m ≠ -1

D. Không có m

Bài giải:

Điều kiện:

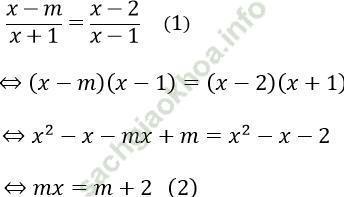
Để phương trình (1) có nghiệm duy nhất thì phương trình (2) có nghiệm duy nhất khác -1 và 1

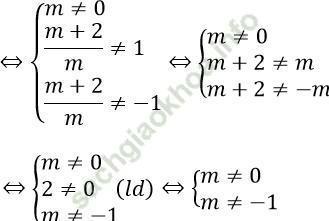
Đáp án: C

Câu 11. Biết phương trình: x - 2 + (x + a)/ (x - 1) = a có nghiệm duy nhất và nghiệm đó là nghiệm nguyên. Tìm nghiệm đó?

A. -2 B. -1 C. 2 D. 0

Bài giải:

Điều kiện: x ≠ 1

Ta có: x - 2 + (x + a)/ (x - 1) = a

⇔ x² - 3x + 2 + x + a = ax - a

⇔ x² - (2 + a)x + 2a + 2 = 0 (2)

Phương trình (1) có nghiệm duy nhất ⇔ phương trình (2) có nghiệm duy nhất khác 1 hoặc phương trình (2) có 2 nghiệm phân biệt trong đó có một nghiệm bằng 1.

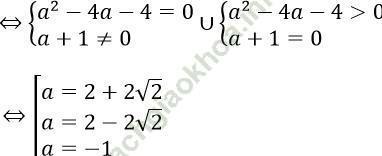
Với a = 2 + 2√ 2 phương trình có nghiệm là: x = 2 + √ 2

Với a = 2 - 2√ 2 phương trình có nghiệm là: x = 2 - √ 2

Với a = -1 phương trình có nghiệm là: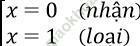

Đáp án: D

Câu 12. Trong các khẳng định sau, khẳng định nào đúng về phương trình:

(x - m)/ (x + 1) = 2

A. m ≠ -1 phương trình (1) có nghiệm là x = -m - 2

B. m = -1 phương trình (1) vô nghiệm

C. Cả A, B đều đúng

D. Cả A, B đều sai

Bài giải:

TXĐ: D = R/ {-1}

Phương trình tương đương với x - m = 2 (x + 1)

⇔ x = -m - 2

Đối chiếu với điều kiện ta xét: -m - 2 ≠ -1 ⇔ m ≠ -1

Kết luận

+ Với m ≠ -1 phương trình (1) có nghiệm là x = -m - 2

+ Với m = -1 phương trình (1) vô nghiệm

Đáp án: C

Câu 13. Tìm điều kiện a, b để phương trình: 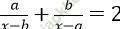(1) có hai nghiệm phân biệt.

A. a ≠ ±2b; a ≠ 0, b ≠ 0

B. 2a ≠ ±b; a ≠ 0, b ≠ 0

C. 3a ≠ ±b; a ≠ 0, b ≠ 0

D. a ≠ ±b; a ≠ 0, b ≠ 0

Bài giải:

TXĐ: D = R/ {a, b}

Ta có: PT (1) ⇔ 2 (x - a)(x - b) = a (x - a) + b (x - b)

⇔ 2x² - 3 (a + b)x + a² + b² + 2ab = 0

⇔ 2x² - 3 (a + b)x + (a + b)² = 0

Phương trình có hai nghiệm là: x₁ = a + b và x₂ = (a + b)/2

Ta có: x₁ ≠ a ⇔ b ≠ 0, x₁ ≠ b

⇔ a ≠ 0, x₂ ≠ a

⇔ x₂ ≠ b

⇔ a ≠ b

x₁ ≠ x₂ ⇔ a+b ≠ (a+b)/2

⇔ a ≠ -b

Vậy với a ≠ ±b; a ≠ 0, b ≠ 0 thì phương trình đã cho có 2 nghiệm phân biệt

Đáp án: D

Câu 14. Trong các khẳng định sau, khẳng định nào đúng về phương trình:

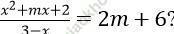
A. m = -5/3 phương trình có nghiệm là x = -2

B. m ≠ -5/3 phương trình có nghiệm là x = 2 và x = -3m - 8

C. Cả A, B đều đúng

D. Cả A, B đều sai

Bài giải:

TXĐ: D = R/ {3}

Phương trình (3) ⇔ x² + mx + 2 = (3-x)(2m+6)

⇔ x² + (3m+4)x - 6m - 16 = 0

⇔ (x - 2)(x + 3m + 8) = 0

⇔

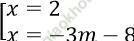
Đối chiếu điều kiện ta xét: -3m - 8 ≠ 3 ⇔ m ≠ -5/3

Kết luận

+) m = -5/3 phương trình (3) có nghiệm là x = -2

+) m ≠ -5/3 phương trình có nghiệm là x = 2 và x = -3m - 8

Đáp án: C

Câu 15. Trong các khẳng định sau, khẳng định nào đúng về phương trình:

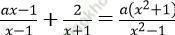
A. Với a ≠ -1 và a ≠ -2 thì phương trình có nghiệm duy nhất x = (a+3)/ (a+1)

B. Với a = -1 hoặc a = -2 thì phương trình vô nghiệm.

C. Cả A, B đều đúng

D. Cả A, B đều sai

Bài giải:

TXĐ: D = R/ {±1}

Phương trình đã cho ⇔ (ax - 1)(x + 1) + 2 (x - 1) = a (x² + 1)

⇔ ax² + ax - x - 1 + 2x - 2 = ax² + a ⇔ (a + 1)x = a + 3

+ Nếu a ≠ -1 thì x = (a + 3)/ (a + 1).

Ta có (a + 3)/ (a + 1) ≠ 1, xét (a + 3)/ (a + 1) ≠ -1

⇔ a ≠ -2

+ Nếu a = -1 thì phương trình vô nghiệm.

Vậy:

Với a ≠ -1 và a ≠ -2 thì phương trình có nghiệm duy nhất x = (a+3)/ (a+1).

Với a = -1 hoặc a = -2 thì phương trình vô nghiệm.

Đáp án: C

Bài trước: Dạng 7: Phương trình chứa ẩn ở mẫu - Chuyên đề Toán 10 Bài tiếp: Dạng 8: Phương trình chứa ẩn dưới dấu căn - Chuyên đề Toán 10