Dạng 10: Giải và biện luận hệ phương trình bậc nhất - Chuyên đề Toán 10
Ví dụ minh họa
Bài 1: Giải hệ phương trình:
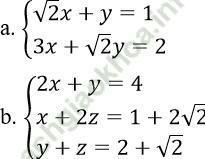
Bài giải:
a. Ta có: y = 1 - √ 2x ⇒ 3x + √ 2 (1 - √ 2. x) = 2
⇒ x = 2 - √ 2 ⇒ y = 3 - 2√ 2
b. Thế y = 4 - 2x vào phương trình y + z = 2 + √ 2 ta được -2x + z = -2 + √ 2
Giải hệ: 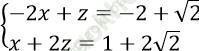 ta được x = 1; z = √ 2 ⇒ y = 2
ta được x = 1; z = √ 2 ⇒ y = 2
Bài 2: Giải hệ phương trình: 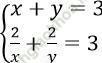
Bài giải:
Điều kiện xác đinh: xy ≠ 0. Khi đó:
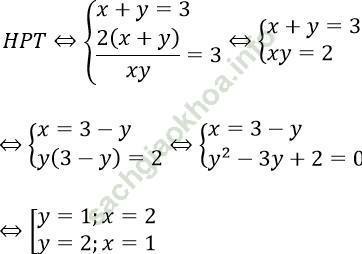
Bài 3: Có bao nhiêu cặp số nguyên (a; b) sao cho hệ phương trình
![]() vô nghiệm
vô nghiệm
Bài giải:
Ta có: ax + y = 2 ⇒ y = 2 - ax
Thay vào phương trình 6x + by = 6 ta có: 6x + b (2 - ax) = 6
⇔ x (6 - ab) + 2b - 6 = 0
Để hệ phương trình đã cho vô nghiệm thì phương trình x (6 - ab) + 2b - 6 = 0 vô nghiệm
Do (a; b) nguyên nên (a; b) = {(6; 1); (1; 6); (-6; -1); (-1; -6); (-2; -3); (-3; -2); (3; 2)}
Bài 4: Gọi (x0; y0; z0) là nghiệm của hệ phương trình: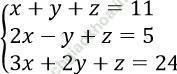
Tính giá trị của biểu thức P = x0y0z0
Bài giải:
Ta có: 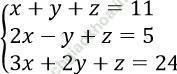
Đặt pt: x + y + z = 11 (1); 2x - y + z = 5 (2); 3x + 2y + z = 24 (3)
Xét phương trình (3) ⇔ z = 24 - 3x - 2y. Thay vào (1) và (2) ta được hệ phương trình:
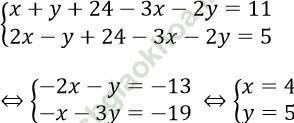
Suy ra z = 24 - 3.4 - 2.5 = 2
Vậy hệ phương trình có nghiệm (x; y; z) = (4; 5; 2) → P = 4.5.2 = 40
Bài 5: Tìm giá trị thực của tham số m để hệ phương trình
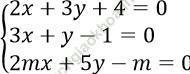 có duy nhất một nghiệm.
có duy nhất một nghiệm.Bài giải:
Từ hệ phương trình đã cho ta suy ra
Hệ phương trình: 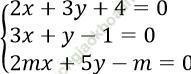 có nghiệm duy nhất khi (1; -2) là nghiệm của phương trình 2mx + 5y - m = 0, tức là 2m. 1 + 5. (-2) - m = 0
có nghiệm duy nhất khi (1; -2) là nghiệm của phương trình 2mx + 5y - m = 0, tức là 2m. 1 + 5. (-2) - m = 0
⇔ m = 10
Vậy với m = 10 hệ phương trình đã cho có duy nhất một nghiệm.
Bài 6: Cho hệ phương trình: ![]() . Tìm các giá trị thích hợp của tham số a để tổng bình phương hai nghiệm của hệ phương trình đạt giá trị nhỏ nhất.
. Tìm các giá trị thích hợp của tham số a để tổng bình phương hai nghiệm của hệ phương trình đạt giá trị nhỏ nhất.
Bài giải:
Ta có:

Đẳng thức xảy ra khi a = 1/2
Vậy với a = 1/2 thỏa mãn điều kiện bài toán.
Bài trước: Bài tập phương trình quy về phương trình bậc hai - Chuyên đề Toán 10 Bài tiếp: Bài tập giải và biện luận hệ phương trình bậc nhất - Chuyên đề Toán 10