Bài tập giải và biện luận hệ phương trình bậc nhất - Chuyên đề Toán 10

Câu 1. Tìm nghiệm của hệ phương trình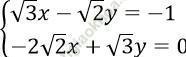

A. (x; y) = (√ 3; -2√ 2)

B. (x; y) = (-√ 3; 2√ 2)

C. (x; y) = (√ 3; 2√ 2)

D. (x; y) = (-√ 3; 2√ 2)

Bài giải:

Đáp án: C

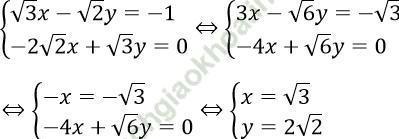
Câu 2. Tìm nghiệm của hệ phương trình: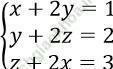

Bài giải:

Đáp án: D

Từ phương trình: z + 2x = 3 => z = 3 - 2x. Thay z vào hai phương trình còn lại ta được hệ phương trình:

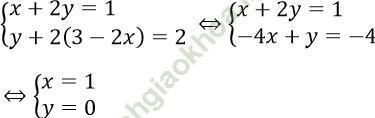
=> z = 3 - 2.1 = 1.

Câu 3. Tìm nghiệm của hệ phương trình: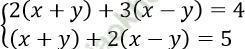

A. (1/2; 13/2) B. (-1/2; -13/2) C. (13/2; 1/2) D. (-13/2; -1/2)

Bài giải:

Đáp án: B

Đặt u = x + y, v = x - y

Khi đó hệ tương đương:

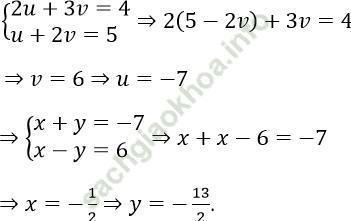
Câu 4. Tìm nghiệm của hệ phương trình: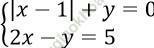

A. x = -3; y = 2

B. x = 2; y = -1

C. x = 4; y = -3

D. x = -4; y = 3

Bài giải:

Đáp án: B

Câu 5. Tìm nghiệm của hệ phương trình: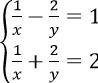

A. (x; y) = (2/3; 4)

B. (x; y) = (-2/3; 4)

C. (x; y) = (2; 4)

D. (x; y) = (-2; -4)

Bài giải:

Đáp án: A

Điều kiện xác định: xy ≠ 0. Đặt 1/x = a; 1/y = b

⇒

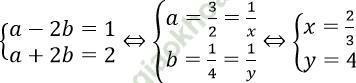
Vậy nghiệm của hệ phương trình là (x; y) = (2/3; 4)

Câu 6. Hệ phương trình: có nghiệm là?

A. (x; y) = (-1; -1/2)

B. (x; y) = (3/4; -2/3)

C. (x; y) = (-3/4; -2/3)

D. (x; y) = (1; 1/2)

Bài giải:

Đáp án: C

Điều kiện xác định: x ≠ y. Khi đó HPT tương đương

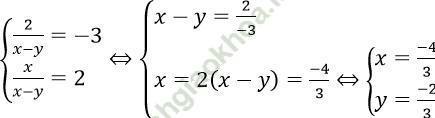
Câu 7. Bộ (x; y; z) = (1; 0; 1) là nghiệm của hệ phương trình nào sau đây?

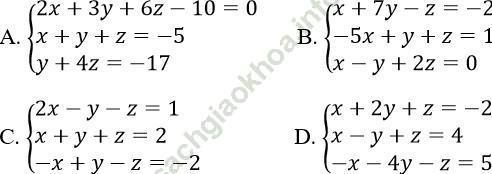
Bài giải:

Đáp án: C

Bằng cách sử dụng máy tính bỏ túi ta được (x; y; z) = (1; 0; 1) là nghiệm của hệ phương trình

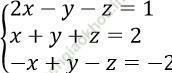
Câu 8. Gọi (x₀; y₀; z₀) là nghiệm của hệ phương trình 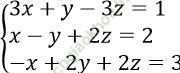. Tính giá trị của biểu thức P = x₀² + y₀² + z₀²

A. P = 1 B. P = 2 C. P = 3 D. P = 14

Bài giải:

Đáp án: C

Ta có: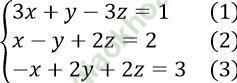

Từ phương trình (2) => x = y - 2z + 2. Thay vào (1), ta được: 3 (y - 2z + 2) + y - 3z = 1

⇔ 4y - 9z = -5 (*)

Phương trình (3) ⇔ x = 2y + 2z - 3. Thay vào (1), ta được: 3 (2y + 2z - 3) + y - 3z = 1

⇔ 7y + 3z = 10 (**)

Từ (*) và (**), ta có: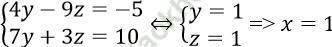

Vậy hệ phương trình có nghiệm (x; y; z) = (1; 1; 1) ⇒ P = 1² + 1² + 1² = 3

Câu 9. Hệ phương trình: 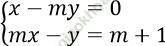có nghiệm duy nhất khi nào?

A. m ≠ 1 B. m ≠ -1 C. m ≠ 0 D. m ≠ ±1

Bài giải:

Đáp án đúng là: D

Hệ pt đã cho có nghiệm duy nhất ⇔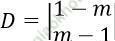

= -1 + m² ≠ 0 ⇔ m ≠ ±1

Câu 10. Cho hệ phương trình 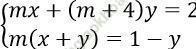. Tìm m để hệ đã cho vô nghiệm.

A. m = 0

B. m = 1 hay m = 2

C. m = -1 hay m = 1/2

D. m = -1/2 hay m = 3

Bài giải:

Đáp án: A

Biến đổi hệ < =>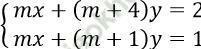

⇒ D = m (m + 1) - m (m + 4) = -3m

Hệ vô nghiệm < => D = 0 ⇒ m = 0

Thử lại thấy m = 0 thoả mãn điều kiện

Câu 11. Với giá trị nào của m thì hai đường thẳng sau trùng nhau (d₁): (m² – 1)x – y + 2m + 5 = 0 và (d₂): 3x – y + 1 = 0

A. m = -2

B. m = 2

C. m = 2 hay m = -2

D. Không có giá trị m

Bài giải:

Đáp án: A

Hai đường thẳng d₁ và d₂ trùng nhau khi

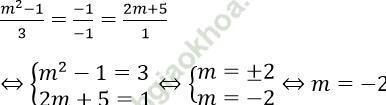
Câu 12. Cho hệ phương trình: 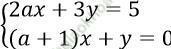. Xét các mệnh đề sau:

I. Hệ phương trình có nghiệm duy nhất khi a ≠ -3

II. Hệ có vô số nghiệm khi a = -3

III. Hệ vô nghiệm khi a = -3

Mệnh đề nào là đúng?

A. Chỉ I B. Chỉ II C. I và II D. I và III

Bài giải:

Đáp án: D

Ta có:

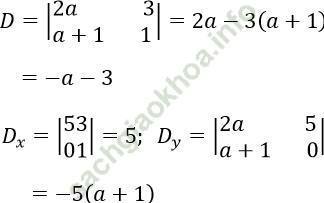
Khi D = -a - 3 ≠ 0⇔ a ≠ -3 khi đó hệ có nghiệm duy nhất.

Khi D = -a - 3 = 0⇔ a = -3 thì D_x = 5 ≠ 0 nên hệ vô nghiệm.

Câu 13. Cho hệ phương trình: 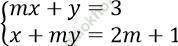. Tìm các giá trị thích hợp của tham số m để hệ phương trình có nghiệm nguyên?

A. m = 0, m = –2

B. m = 1, m = 2, m = 3

C. m = 0, m = 2

D. m = 1, m = –3, m = 4

Bài giải:

Đáp án: A

Ta có: D = m² - 1, D_x = m - 1, D_y = 2m² + m - 3

Hệ phương trình có nghiệm x = D_x/D = 1/ (m+1), y = D_y/D = (2m-1)/ (m+1)

Hệ phương trình có nghiệm nguyên khi m = 0; m = -2

Câu 14. Cho hệ phương trình: 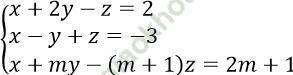. Tìm m để hệ phương trình có nghiệm?

A. m ≠ -4 B. m = -4 C. m = 3 D. m ≠ -4.

Bài giải:

Đáp án: A

Ta có:

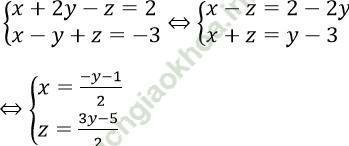
Thế vào (3) ta có:

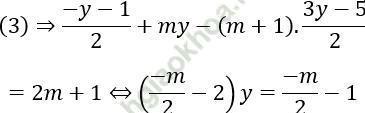
Hệ phương trình có nghiệm ⇔ (-m)/2 - 2 ≠ 0 ⇔ m ≠ -4

Câu 15. Tìm giá trị thực của tham số m để hệ phương trình: 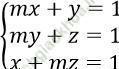vô nghiệm.

A. m = -1 B. m = 0 C. m = 1 D. m = 1

Bài giải:

Đáp án: A

Từ hệ phương trình đã cho suy ra z = 1 - my

Thay vào hai phương trình còn lại, ta được:

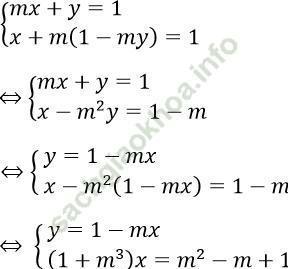
Để hệ phương trình đã cho vô nghiệm thì:

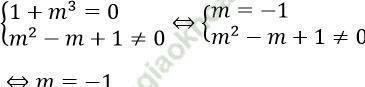
Câu 16. Các cặp nghiệm (x; y) của hệ phương trình: 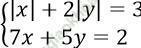là:

A. (1; 1) hay (11/19; 23/19)

B. (-1; -1) hay (-11/19; 23/19)

C. (1; -1) hay (-11/19; 23/19)

D. (-1; 1) hay (11/19; 23/19)

Bài giải:

Đáp án: C

Khi x, y ≥ 0 thì hệ trở thành

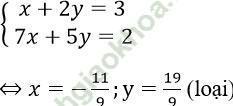
Khi x, y < 0 thì hệ trở thành

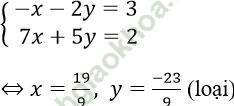
Khi x ≥ 0, y < 0 thì hệ trở thành

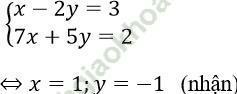
Khi x < 0, y ≥ 0 thì hệ trở thành

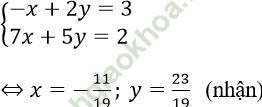
Câu 17. Cho hệ phương trình: 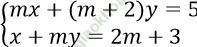. Tìm m để hệ phương trình có nghiệm âm?

A. m < 2 hay m > 5/2

B. 2 < m < 5/2

C. m < -5/2 hay m > -2

D. -5/2 < m < -1

Bài giải:

Đáp án: D

Ta có: D = m² - m - 2, D_x = -2m² - 2m - 6, D_y = 2m² + 3m - 5

Để hệ phương trình có nghiệm thì: D ≠ 0 ⇔ m ≠ -1; m ≠ 2

Nghiệm của hệ là:

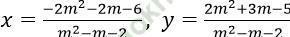
Câu 18. Cho hệ phương trình: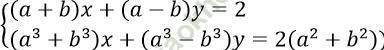

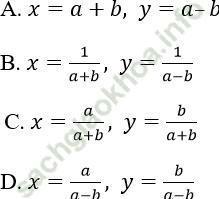
. Với a ≠ ±b, a. b ≠ 0, hệ có nghiệm duy nhất bằng:

Bài giải:

Đáp án: B

Ta có: D = (a + b)(a³ - b³) - (a³ + b³) (a - b) = 2ab (a² - b²)

D_x = 2 (a³ - b³) - 2 (a² + b²) (a - b) = 2ab (a - b)

D_y = (a - b)2 (a² + b²) - 2 (a³ - b³)= 2ab (a + b)

Hệ có nghiệm:

Câu 19. Có ba lớp học sinh 10A, 10B, 10C gồm 128 em cùng tham gia lao động trồng cây. Mỗi em lớp 10A trồng được 3 cây bạch đàn và 4 cây bàng. Mỗi em lớp 10B trồng được 2 cây bạch đàn và 5 cây bàng. Mỗi em lớp 10C trồng được 6 cây bạch đàn. Cả ba lớp trồng được là 476 cây bạch đàn và 375 cây bàng. Hỏi mỗi lớp có bao nhiêu học sinh?

A. 10A có 40 em, lớp 10B có 43 em, lớp 10C có 45 em

B. 10A có 45 em, lớp 10B có 43 em, lớp 10C có 40 em

C. 10A có 45 em, lớp 10B có 40 em, lớp 10C có 43 em

D. 10A có 43 em, lớp 10B có 40 em, lớp 10C có 45 em

Bài giải:

Đáp án: A

Gọi x, y, z lần lượt là số học sinh của lớp 10A, 10B, 10C.

Điều kiện: x, y, z nguyên dương

Theo đề bài, ta có hệ phương trình:

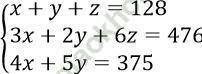
Giải hệ => x = 40, y = 43, z = 45

Câu 20. Một đoàn xe tải chở 290 tấn xi măng cho một công trình xây đập thủy điện. Đoàn xe gồm ba loại, xe chở 3 tấn, xe chở 5 tấn và xe chở 7,5 tấn. Nếu dùng tất cả xe 7,5 tấn chở ba chuyến thì được số xi măng bằng tổng số xi măng do xe 5 tấn chở ba chuyến và xe 3 tấn chở hai chuyến. Hỏi số xe mỗi loại?

A. 18 xe chở 3 tấn, 19 xe chở 5 tấn và 20 xe chở 7,5 tấn

B. 20 xe chở 3 tấn, 19 xe chở 5 tấn và 18 xe chở 7,5 tấn

C. 19 xe chở 3 tấn, 20 xe chở 5 tấn và 18 xe chở 7,5 tấn

D. 20 xe chở 3 tấn, 18 xe chở 5 tấn và 19 xe chở 7,5 tấn

Bài giải:

Đáp án: B

Gọi x là số xe tải chở 3 tấn, y là số xe tải chở 5 tấn, z là số xe tải chở 7,5 tấn.

Điều kiện xác định: x, y, z nguyên dương

Theo bài ra ta có:

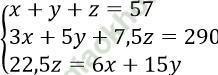
Giải hệ => x = 20, y = 19, z = 18

Bài trước: Dạng 10: Giải và biện luận hệ phương trình bậc nhất - Chuyên đề Toán 10 Bài tiếp: Dạng 11: Các dạng hệ phương trình đặc biệt - Chuyên đề Toán 10