Bài tập tìm tập xác định của phương trình - Chuyên đề Toán 10
Câu 1. Hai phương trình được gọi là tương đương khi
A. Có cùng dạng phương trình
B. Có cùng tập xác định
C. Có cùng tập hợp nghiệm.
D. Cả A, B, C đều đúng
Bài giải:
Đáp án: C
Câu 2. Trong các khẳng định sau, khẳng định nào đúng?
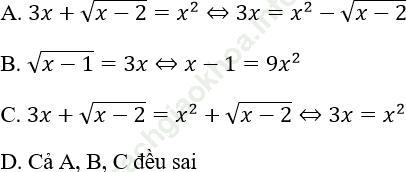
Bài giải:
Đáp án: A
Câu 3. Phương trình (x2 + 1)(x – 1)(x + 1) = 0 tương đương với phương trình:
A. x - 1 = 0
B. x + 1 = 0
C. x2 + 1 = 0
D. (x - 1)(x + 1) = 0
Bài giải:
Đáp án: D
Vì hai phương trình có cùng tập nghiệm T = {±1}.
Câu 4. Phương trình: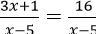 tương đương với phương trình:
tương đương với phương trình:
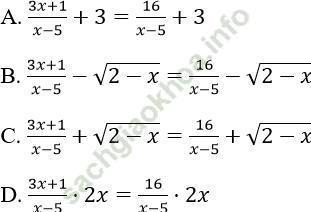
Bài giải:
Đáp án: A
Vì hai phương trình có cùng tập nghiệm T = {5}.
Câu 5. Cho phương trình 2x2 - x = 0 (1). Trong các phương trình sau đây, phương trình nào không phải là hệ quả của phương trình (1)?
A. 2x - x/ (1 - x) = 0
B. 4x3 - x = 0
C. (2x2 - x)2 = 0
D. x2 - 2x + 1 = 0
Bài giải:
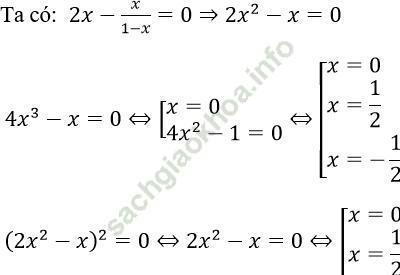
⇒ Đáp án: D vì x2 - 2x + 1 = 0 ⇔ x = 1 (không phải là nghiệm của (1).
Câu 6. Cho phương trình và
và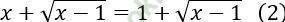
Khẳng định đúng nhất trong các khẳng định sau là:
A. (1) và (2) tương đương
B. (2) là phương trình hệ quả của (1)
C. (1) là phương trình hệ quả của (2)
D. Cả A, B, C đều đúng
Bài giải:
Ta có: (1) ⇔ x = 2 hoặc x = 1. Và (2) ⇔ x = 1
=> (1) là phương trình hệ quả của (2).
Đáp án: C
Câu 7. Cho phương trình: 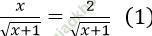 và x2 − x − 2 = 0 (2)
và x2 − x − 2 = 0 (2)
Khẳng định đúng nhất trong các khẳng định sau là:
A. (1) và (2) tương đương
B. (2) là phương trình hệ quả của (1)
C. (1) là phương trình hệ quả của (2)
D. Cả A, B, C đều đúng
Bài giải:
Ta có: (1)⇔ x = 2 (2) ⇔ x = -1 ∪ x = 2
Vậy (2) là phương trình hệ quả của (1)
Đáp án: B.
Câu 8. Khi giải phương trình |x - 2| = 2x - 3 (1), một học sinh tiến hành theo các bước sau:
Bước 1: Bình phương hai vế của phương trình (1) ta được:
x2 - 4x + 4 = 4x2 - 12x + 9 (2)
Bước 2: Khai triển và rút gọn (2) ta được: 3x2 - 8x + 5 = 0
Bước 3: (2)⇔ x = 1 ∪ x = 5/3
Bước 4: Vậy phương trình có nghiệm là: x = 1 và x = 5/3
Cách giải trên sai từ bước nào?
A. Sai ở bước 1.
B. Sai ở bước 2.
C. Sai ở bước 3.
D. Sai ở bước 4.
Bài giải:
Vì phương trình (2) là phương trình hệ quả nên ta cần thay nghiệm vào phương trình (1) để thử lại
Đáp án: D
Câu 9. Khi giải phương trình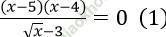 một học sinh tiến hành theo các bước sau:
một học sinh tiến hành theo các bước sau:
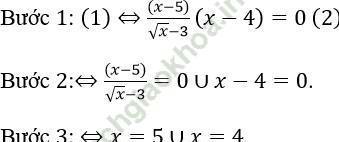
Bước 4: Vậy phương trình có tập nghiệm là: T = {5; 4}
Cách giải trên sai từ bước nào?
A. Sai ở bước 1.
B. Sai ở bước 2.
C. Sai ở bước 3.
D. Sai ở bước 4.
Bài giải:
Vì biến đổi tương đương mà chưa đặt điều kiện
Đáp án: B
Câu 10. Khi giải phương trình: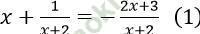 một học sinh tiến hành theo các bước sau:
một học sinh tiến hành theo các bước sau:
Bước 1: ĐK: x ≠ -2
Bước 2: với điều kiện trên (1) ⇔ x (x + 2) + 1 = - (2x + 3) (2)
Bước 3: (2)⇔ x2 + 4x + 4 = 0 ⇔ x = -2
Bước 4: Vậy phương trình có tập nghiệm là: T = {-2}
Cách giải trên sai từ bước nào?
A. Sai ở bước 1.
B. Sai ở bước 2.
C. Sai ở bước 3.
D. Sai ở bước 4.
Bài giải:
Vì không kiểm tra điều kiện
Đáp án: D
Câu 11. Phương trình (x - 4)2 = x - 2 là phương trình hệ quả của phương trình nào sau đây?
A. x - 4 = x - 2
B. √ (x - 2) = x - 4
C. √ (x - 4) = √ (x - 2)
D. √ (x - 4) = x - 2
Bài giải:
Ta có √ (x-2) = x-4 ⇒ (x-4)2 = x-2
Đáp án: B.
Câu 12. Phương trình x2 = 3x tương đương với phương trình:
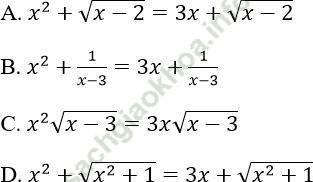
Bài giải:
Vì hai phương trình có cùng tập nghiệm T = {0; 3}
Đáp án: D.
Câu 13. Phương trình: 3x - 7 = √ (x - 6) tương đương với phương trình:
A. (3x - 7)2 = x - 6
B. √ (3x - 7) = x - 6
C. (3x - 7)2 = (x - 6)2
D. √ (3x - 7) = √ (x - 6)
Bài giải:
Đáp án: A.
Ta có: 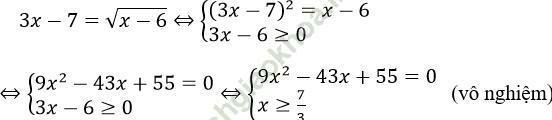
Ta có (3x - 7)2 = x - 6 ⇔ 9x2 - 43x + 55 = 0 vô nghiệm
Câu 14. Cho hai phương trình x2 + x + 1 = 0 (1) và √ (1-x) = √ (x-1) + 2 (2). Khẳng định đúng nhất trong các khẳng định sau là:
A. (1) và (2) tương đương.
B. Phương trình (2) là phương trình hệ quả của phương trình (1).
C. Phương trình (1) là phương trình hệ quả của phương trình (2).
D. Cả A, B, C đều đúng.
Bài giải:
Đáp án: D
Câu 15. Chỉ ra khẳng định sai?
A. √ (x-2) = 3√ (2-x) ⇔ x-2 = 0
B. √ (x-3) = 2 ⇒ x-3 = 4
C. |x-2| = 2x + 1 ⇔ (x-2)2 = (2x+1)2
D. x2 = 1 ⇔ x = ±1
Bài giải:
Đáp án: C
Câu 16. Tập xác định của phương trình: 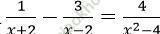 là:
là:
A. (2; +∞) B. R\ {-2; 2} C. [2; +∞) D. R
Bài giải:
Đáp án: B
Điều kiện xác định:
Vậy TXĐ: R\ {-2; 2}
Câu 17. Điều kiện xác định của phương trình √ (2x - 1) = 4x + 1 là:
A. (3; +∞) B. [1/2; +∞) C. [1; +∞) D. [3; +∞)
Bài giải:
Đáp án: B
Điều kiện xác định: 2x - 1 ≥ 0 ⇔ x ≥ 1/2
Câu 18. Điều kiện xác định của phương trình √ (3x - 2) + √ (4 - 3x) = 1 là:
A. (4/3; +∞) B. (2/3; 4/3) C. R\ {2/3; 4/3} D. [2/3; 4/3]
Bài giải:
Đáp án: D
Điều kiện xác định: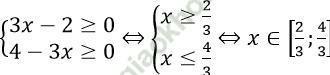
Câu 19. Điều kiện xác định của phương trình √ (x-1) + √ (x-2) = √ (x-3) là:
A. (3; +∞) B. [2; +∞) C. [1; +∞) D. [3; +∞)
Bài giải:
Đáp án: B
Điều kiện xác định: 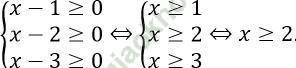
Câu 20. Tập xác định của phương trình: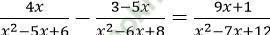 là:
là:
A. (4; +∞) B. R\ {2; 3; 4} C. R D. R\ {4}
Bài giải:
Đáp án: B.
Điều kiện xác định:
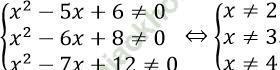
Vậy TXĐ: R\ {2; 3; 4}.
Bài trước: Dạng 1: Tìm tập xác định của phương trình - Chuyên đề Toán 10 Bài tiếp: Dạng 2: Giải phương trình bằng phương pháp biến đổi tương đương - Chuyên đề Toán 10