Bài tập phương trình chứa ẩn dưới dấu căn - Chuyên đề Toán 10

Câu 1. Tập nghiệm S của phương trình √ (x² - 4) = x - 2 là:

A. S = {0; 2} B. S = {2} C. S = {0} D. S = ∅

Bài giải:

Ta có:

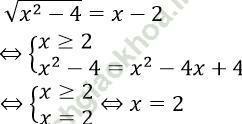
Đáp án: B

Câu 2. Tính tổng các nghiệm của phương trình: (x - 2)√ (2x + 7) = x² - 4.

A. 0 B. 1 C. 2 D. 3

Bài giải:

Điều kiện xác định của phương trình: 2x + 7 ≥ 0 ⇔ x ≥ -7/2

Ta có: (x - 2)√ (2x + 7) = x² - 4

⇔ (x - 2)√ (2x + 7) = (x - 2)(x + 2)

Vậy phương trình đã cho có hai nghiệm x = 1, x = 2 nên tổng 2 nghiệm của phương trình là: 1 + 2 = 3

Đáp án: D

Câu 3. Phương trình: 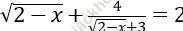có tất cả bao nhiêu nghiệm?

A. 0 B. 1 C. 2 D. 3

Bài giải:

Điều kiện xác định của phương trình: 2 - x ≥ 0 ⇔ x ≤ 2

Từ phương trình đã cho ta được

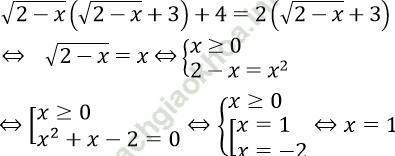
Đối chiếu nghiệm với điều kiện x < 2 => x = 1 là nghiệm duy nhất của phương trình

Đáp án: B

Câu 4. Số nghiệm của phương trình là:

A. 0 B. 1 C. 2 D. 3

Bài giải:

Ta có:

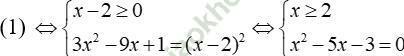
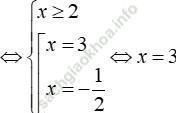
Câu 5. Tìm số nghiệm của phương trình (x + 5)(2 - x) = 3√ (x² + 3x) (1)

A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. 4 nghiệm

Bài giải:

Phương trình (1) ⇔ x² + 3x + 3√ (x² + 3x) - 10 = 0

Đặt t = √ (x² + 3x), t ≥ 0. Phương trình đã cho trở thành

t² + 3t - 10 = 0 ⇔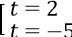

Vì t ≥ 0 ⇒ t = -5 (loại), t = 2 (thỏa mãn).

Thay vào ta có √ (x² + 3x) = 2

⇔ x² + 3x - 4 = 0 ⇔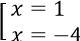

Vậy phương trình có 2 nghiệm là x = 1 và x = -4

Đáp án: B

Câu 6. Cho phương trình: 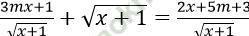. Để phương trình có nghiệm điều kiện để thỏa mãn tham số m là... ?

A. 0 B. 1 C. 2 D. 3

Bài giải:

Điều kiện: x ≥ 4

Phương trình < => √ (x - 4)(x² - 3x + 2) = 0 ⇔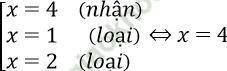

Đáp án: B

Câu 7. Số nghiệm của phương trình √ (x² + 2x + 4) = √ (2 - x)

A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. 4 nghiệm

Bài giải:

Điều kiện: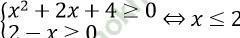

Với điều kiện đó phương trình tương đương với

x² + 2x + 4 = 2 - x ⇔ x² + 3x + 2 = 0 ⇔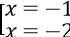

Đối chiếu với điều kiện ta thấy phương trình có 2 nghiệm là: x = -1 và x = -2

Đáp án: B

Câu 8. Tìm số nghiệm của phương trình x - √ (2x - 5) = 4?

A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. 4 nghiệm

Bài giải:

Điều kiện: 2x - 5 ≥ 0 ⇔ x ≥ 5/2

Phương trình: x - √ (2x-5) = 4

⇔ √ (2x - 5) = x - 4 (*)

+) Trường hợp 1: Với x - 4 < 0 ⇔ x < 4 ta có VT (*) ≥ 0, VP (*) < 0 => Phương trình vô nghiệm.

+) Trường hợp 2: Với x - 4 ≥ 0 ⇔ x ≥ 4 ta có hai vế không âm nên phương trình (*) tương đương

2x - 5 = (x-4)²

⇔ x² - 10x + 21 = 0

⇔

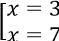
Đối chiếu với điều kiện x ≥ 4 và điều kiện xác định => x = 7 là nghiệm

Vậy phương trình có 1 nghiệm là x = 7

Đáp án: A

Câu 9. Tìm số nghiệm của phương trình:

A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. 4 nghiệm.

Bài giải:

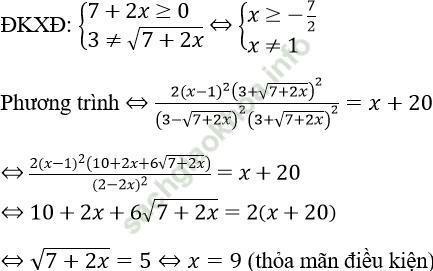
Vậy phương trình có 1 nghiệm là: x = 9

Đáp án: A

Câu 10. Tìm số nghiệm của phương trình: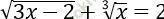

A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. 4 nghiệm

Bài giải:

ĐKXĐ: x ≥ 2/3

Nhẩm ta thấy x = 1 là nghiệm của phương trình nên ta tách như sau

Phương trình (*) ⇔ x = 1 (thỏa mãn điều kiện)

Vậy phương trình có nghiệm duy nhất x = 1

Đáp án: A

Câu 11. Tìm số nghiệm của phương trình: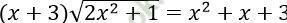

A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. 4 nghiệm

Bài giải:

Câu 11. Chọn B

Ta thấy x = -3 không là nghiệm của phương trình

Xét x ≠ -3, phương trình

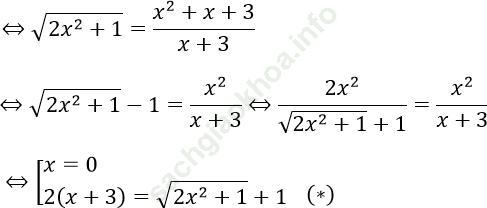
Phương trình (*) ⇔ √ (2x² + 1) = 2x + 5

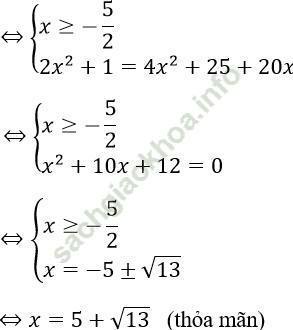
Vậy phương trình đã cho có nghiệm x = 0 và x = -5 + √ 13

Câu 12. Tìm số nghiệm của phương trình: .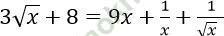

A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. 4 nghiệm

Bài giải:

Câu 12. Chọn B

ĐKXĐ: x > 0

Phương trình tương đương với

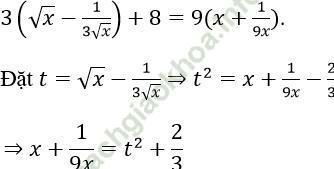
Phương trình trở thành:

3t + 8 = 9 (t² + 2/3) ⇔ 9t² - 3t - 2 = 0 ⇔

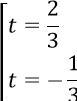
Vậy phương trình có nghiệm là x = 1 và x = (7-√ 13)/18

Câu 13. Tìm số nghiệm của phương trình: .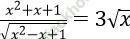

A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. 4 nghiệm

Bài giải:

Câu 13. Chọn C

ĐKXĐ: x ≥ 0

Dễ thấy x = 0 không phải là nghiệm của phương trình

Xét x > 0, phương trình ⇔ x² + x + 1 = 3√ x. √ (x² - x + 1)

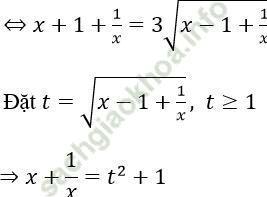
Phương trình trở thành t² + 2 = 3t ⇔ t² - 3t + 2 = 0 ⇔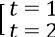

+ Với t = 1 ta có √ (x - 1 + 1/x) = 1 ⇔ x² - x + 1 = x ⇔ x = 1 (thỏa mãn)

+ Với t = 2 ta có √ (x - 1 + 1/x) = 2 ⇔ x² - 5x + 1 = 0 ⇔ x = (5 ± √ 21)/2

Vậy phương trình có nghiệm là x = (5 ± √ 21)/2 và x = 1

Câu 14. Tìm số nghiệm của phương trình:

A. 1 nghiệm B. 2 nghiệm C. 3 nghiệm D. 4 nghiệm

Bài giải:

Điều kiện: x ≥ 1/4

Đặt t = √ (4x - 1), t ≥ 0 ⇒ x = (t² + 1)/4

Phương trình trở thành

⇔ 4t + t⁴ + 2t² + 1 - 6 (t² + 1) + 4 = 0

⇔ t⁴ - 4t² + 4t - 1 = 0

⇔ (t - 1)(t³ + t² - 3t + 1) = 0

(t - 1)²(t² + 2t - 1) = 0

⇒

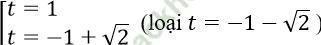
Với t = 1 ta có 1 = √ (4x - 1) ⇔ x = 1/2

Với t = -1 + √ 2 ta có -1 + √ 2 = √ (4x - 1)

⇔ 4x - 1 = 3 - 2√ 2

⇔ x = (2 - √ 2)/2

Vậy phương trình có hai nghiệm x = 1/2 và x = (2 - √ 2)/2

Đáp án: B

Câu 15. Tìm giá trị của m để phương trình √ (x² + mx + 2) = 2x + 1 có hai nghiệm phân biệt?

A. m ≥ 3/2 B. m ≥ -9/2 C. m ≥ 9/2 D. m ≥ -3/2

Bài giải:

Phương trình ⇔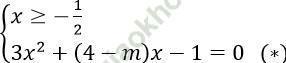

Để phương trình đã cho có 2 nghiệm thì phương trình (*) có hai nghiệm phân biệt lớn hơn hoặc bằng -1/2 ⇔ Đồ thị hàm số y = 3x² + (4-m)x - 1 trên [-1/2; +∞) cắt trục hoành tại hai điểm phân biệt.

Xét hàm số: y = 3x² + (4 - m)x - 1 trên [-1/2; +∞).

Ta có: -b/2a = (m - 4)/6

+ Trường hợp 1: Nếu (m - 4)/6 ≤ -1/2 ⇔ m ≤ 1 thì hàm số đồng biến trên [-1/2; +∞) nên m ≤ 1 không thỏa mãn yêu cầu bài toán.

+ Trường hợp 2: Nếu (m - 4)/6 > -1/2 ⇔ m > 1:

Ta có bảng biến thiên

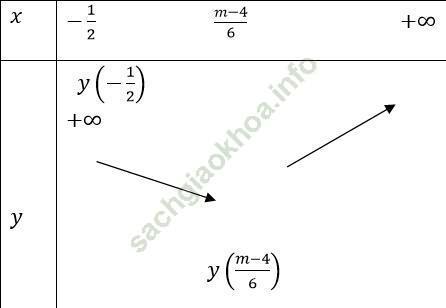
Từ bảng biến thiên suy ra đồ thị hàm số y = 3x² + (4 - m)x - 1 trên [-1/2; +∞) cắt trục hoành tại hai điểm phân biệt

⇔ y (-1/2) ≥ 0 > y ((m - 4)/6)

⇔ (2m - 9)/4 ≥ 0 > (1/12)(-m² + 8m - 28) (1)

Vì -m² + 8m - 28 = - (m - 4)² - 12 < 0, ∀ m nên (1) ⇔ 2m - 9 ≥ 0

⇔ m ≥ 9/2 (thỏa mãn m > 1)

Vậy m ≥ 9/2 là giá trị cần tìm

Đáp án: C

Bài trước: Dạng 8: Phương trình chứa ẩn dưới dấu căn - Chuyên đề Toán 10 Bài tiếp: Dạng 9: Các dạng phương trình quy về phương trình bậc hai - Chuyên đề Toán 10