Dạng 1: Cách xác định tập hợp - Chuyên đề Toán 10

Cách xác định, cách viết tập hợp hay, chi tiết

Phương pháp giải

1: Với tập hợp A, ta có 2 cách:

Cách 1: Liệt kê các phần tử của A: A= {a₁; a₂; a₃;.. }

Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của A.

2: Tập hợp con

Nếu mọi phần tử của tập hợp A đều là phần tử của tập hợp B thì ta nói A là một tập hợp con của B, kí hiệu: A ⊂ B.

A ⊂ B ⇔ ∀ x: x ∈ A ⇒ x ∈ B.

A ⊄ B ⇔ ∀ x: x ∈ A ⇒ x ∉ B.

Tính chất:

1) A ⊂ A với mọi tập A.

2) Nếu A ⊂ B và B ⊂ C thì A ⊂ C.

3) ∅ ⊂ A với mọi tập hợp A.

Ví dụ minh họa

Ví dụ 1: Viết mỗi tập hợp sau bằng cách liệt kê các phần tử của nó:

a) A = {x ∈ R| (2x - x²) (2x² - 3x - 2) = 0}.

b) B = {n ∈ N|3 < n² < 30}.

Bài giải:

a) Ta có: (2x - x²) (2x² - 3x - 2) = 0

⇔

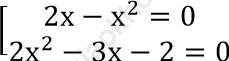
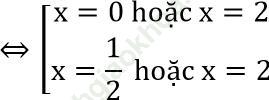
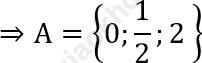
b) 3 < n² < 30 ⇒ √ 3 < |n| < √ 30

Do n ∈ N nên n ∈ {2; 3; 4; 5}

⇒ B = {2; 3; 4; 5}.

Ví dụ 2: Viết mỗi tập hợp sau bằng cách chỉ rõ tính chất đặc trưng cho các phần tử của nó:

a) A = {2; 3; 5; 7}

b) B = {-3; -2; -1; 0; 1; 2; 3}

c) C = {-5; 0; 5; 10; 15}.

Bài giải:

a) A là tập hợp các số nguyên tố nhỏ hơn 10.

b) B là tập hơp các số nguyên có giá trị tuyệt đối không vượt quá 3.

B = {x ∈ Z||x| ≤ 3}.

c) C là tập hợp các số nguyên n chia hết cho 5, không nhỏ hơn - 5 và không lớn hơn 15.

C = {n ∈ Z|-5 ≤ n ≤ 15; n ⋮ 5}.

Ví dụ 3: Cho tập hợp A có 3 phần tử. Cho biết số tập con của tập hợp A?

Bài giải:

Giả sử tập hợp A = {a; b; c}. Các tập hợp con của A là:

∅, {a}, {b}, {c}, {a; b}, {b; c}, {c; a}, {a; b; c}

Tập A có 8 phần tử

Lưu ý: Tổng quát, nếu tập A có n phần tử thì số tập con của tập A là 2² phần tử.

Ví dụ 4: Cho hai tập hợp M = {8k + 5 |k ∈ Z}, N = {4l + 1 | l ∈ Z}. Cho biết khẳng định nào sau đây là đúng?

A. M ⊂ N	B. N ⊂ M
C. M=N	D. M= ∅, N= ∅

Bài giải:

Ta có, tập hợp M ≠ ∅ và N ≠ ∅

Giả sử x là một phần tử bất kì của tập M, ta có x = 8k + 5 (k ∈ Z)

Khi đó, ta có thể viết x = 8k + 5 = 4 (2k + 1) + 1 = 4l + 1 với l = 2k + 1 ∈ Z do k ∈ Z.

=> x ∈ N.

Vậy ∀ x ∈ M ⇒ x ∈ N hay M ⊂ N.

Mặt khác ta có: 1 ∈ N nhưng 1 ∉ M nên N ⊄ M.

=> M ≠ N

Vậy M ⊂ N.

Bài tiếp: Dạng 2: Các phép toán trên tập hợp - Chuyên đề Toán 10